Channels and Linear Temporal Logic
The solutions to exercises 1--4 can be found here.
Exercise 1
Channels are useful when modelling distributed systems. In
Promela a channel has a capacity and a message type.
chan myChan = [0] of { byte }
This simple example specifies a channel called myChan with 0 capacity, making
it a rendezvous channel. The messagetype in this case is byte.
Now create two processes. The first process sends the numbers 0 through 9 onto the channel. The
second process reads the values of the channel and outputs them.
Launch in web-interface
Exercise 2
Is it possible that process p does not read from the channel at all?
chan com = [0] of {byte}
byte value = 0;
proctype p() {
byte i = 0;
do
:: if
:: i >= 5 -> break
:: else -> printf("Doing something else\n");
i ++
fi
:: com ? value ;
printf("p received: %d\n",value)
od
}
init {
atomic {
run p()
}
end:
com ! 100;
}
Launch in web-interface
Exercise 3
Model a system having 5 clients and 2 servers where a client cannot
send another request before their previous one was processed by a
server. The suggested solution uses buffered channels and describes
the behaviour of the server processes. Complete the solution for the
client processes.
chan request = [2] of { byte, chan};
chan reply[5] = [2] of { byte };
active [2] proctype Server() {
byte client;
chan replyChannel;
do
:: request ? client, replyChannel ->
printf("Client %d processed by server %d\n", client, _pid);
replyChannel ! _pid
od
}
proctype Client(byte id) {
...
}
init {
...
}
Launch in web-interface
Exercise 4
Model an office where two computer systems are hooked up to a single printer.
Model the computer systems such that they have mutual exclusion on the printer.
The printer can be modeled as the number of jobs it has.
The two systems can communicate with each other via a rendezvous channel.
Verify that it is never the case that both systems print at the same time.
Exercise 5
Consider a crossing of two streets with one traffic light (nr 1) controlling
the north-to-south direction and one (nr 2) for the west-to-east
direction. Assume you have the following propositional variables:
\(\mathit{R1}\) (traffic light 1 is red), \(\mathit{G1}\) (traffic light 1 is green),
\(\mathit{R2}\) (traffic light 2 is red), \(\mathit{G2}\) (traffic light 2 is green).
Give LTL formulas formalising the following properties:
- Both traffic lights are never green at the same time.
- Each traffic light will become eventually green at any time.
- Traffic light 1 stays red until traffic light 2 has switched
to red.
Does the following run satisfy this last property:
\(\{\mathit{R1}, \mathit{G2}\} \rightarrow \{\mathit{R1}, \mathit{G2}\} \rightarrow \ldots\) (i.e., all states of the run
interpret \(\mathit{R1}\) as true and \(\mathit{G2}\) as true and all others as false)?
Answers:
- \(\Box(\neg \mathit{G1} \vee \neg \mathit{G2})\)
- \(\Box(\Diamond \mathit{G1} \wedge \Diamond \mathit{G2})\)
- \(\mathit{R1} ~ \mathcal{U} ~ \mathit{R2}\), no because \(\mathit{R2}\) bever becomes true
Comment for exercise 6+7+8
If you want, you can use GOAL to check your own solutions.
With GOAL you can
- Check equivalence between ω-regular expressions and Büchi automata.
- Check equivalence between LTL formulae and Büchi automata.
To check equivalence between ω-regular expressions and Büchi automata proceed as follows:
- Draw the automaton. To create a new automaton click File->New->Finite Automaton->Büchi word automaton).
- Important: Before adding any transitions, convert the type of alphabet of the automaton to classic. Click Automaton->Alphabet->Convert Alphabet Type. In the new window click ok. If the alphabet is correctly changed, in the bottom row of the window, you will see Büchi FSA (Classical Alphabet).
- Add the nodes and the transitions to the automaton.
- Write the ω-regular expression, click File->New->Algebraic Expression/Logic Formula->ω-Regular Expression.
- Convert the ω-regular expression into an automaton. Click Formula->Translate ORE to NBW.
- Check equivalence of the two automata. Go to the tab of the generated automata. From there click Automaton->Equivalence->With An Automaton. Finally, select the tab with the automaton you drew in (1).
To check equivalence between LTL formulae and Büchi automata proceed as follows:
- Draw the automaton. To create a new automaton click File->New->Finite Automaton->Büchi word automaton).
- Make sure your automaton is using the propositional alphabet. It is the default alphabet for Büchi word automaton. To make sure, check the bottom row of the window. You should see Büchi FSA (Propositional Alphabet). If not, follow the same steps as in (2) above before adding any transition to the automaton.
- Add the nodes and the transitions to the automaton. Note that the tool will simplify the transitions between two nodes as you add them. Furthermore, remember that here we label transitions with the set of propositions that are true, in the tool, however, you need to specify also the propositions that are false, e.g., for a propositional alphabet {p,q} a transition labelled with {p} will be inserted in the tool as "p ~q".
- Check equivalence with LTL formula. Click on Automaton->Equivalence->With A Formula. In the popup window insert the LTL formula and click Ok.
If everything is fine, a dialog pops up telling that they are equivalent; otherwise, the dialog shows you a counterexample.
IMPORTANT NOTE: As mention earlier the program has a different way to label the transitions. Refer to the documentation (Help -> Help contents) to understand in what they differ.
Exercise 6
Which language is accepted by the following Büchi automata?
-
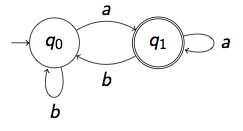 Answer: \((b^{*}a)^{\omega}\)
Answer: \((b^{*}a)^{\omega}\)
-
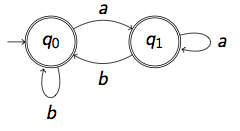 Answer: \((a+b)^{\omega}\)
Answer: \((a+b)^{\omega}\)
-
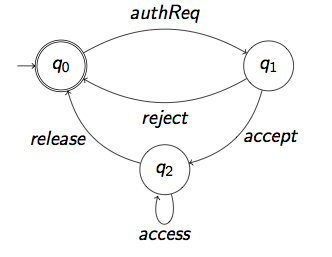 Answer: \((\mathit{authReq}~(\mathit{reject} + \mathit{accept}~\mathit{access}^{*}~\mathit{release}))^{\omega}\)
Answer: \((\mathit{authReq}~(\mathit{reject} + \mathit{accept}~\mathit{access}^{*}~\mathit{release}))^{\omega}\)
Exercise 7
Consider the following LTL formulas and their corresponding Büchi
automata. State whether these formulas accept the same language or not.
If not, provide a counter-example in the form of a word which is accepted
by the LTL formula but not by the automaton, or vice versa.
| 1. Liveness property: \(\Box (p \implies \Diamond q)\) |
|
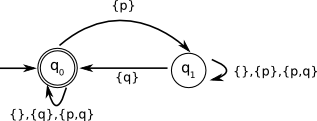 |
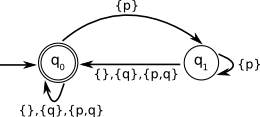
| 2. Weak fairness: \(\Diamond \Box p \implies \Box \Diamond q\) |
|
 |
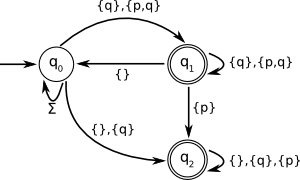
| 3. Strong fairness: \(\Box \Diamond p \implies \Box\Diamond q\) |
|
 |
Answers:
- Incorrect, the automaton stays in \(q_{1}\) when \(p\)
is false but \(q\) is true. A word that is accepted by the LTL
formula is \(\{p\},\{p,q\},\{\},\{\},\{\},\ldots\) but this is not accepted
by the automaton.
- Correct.
- Incorrect, there is an unnecessary transition from \(q_1\)
to \(q_2\). The automaton accepts the word
\(\{q\},\{p\},\{p\},\{p\},\{p\},\ldots\) but this is not accepted by the
LTL formula.
Exercise 8
Consider the largest language formed with the Vocabulary \(V = \{a,b,c\}\) such that for each word of the language the following holds:
- \(a\) appears a finite number of times
- \(b\) appears infinitely often
- a \(b\) cannot immediately follow an \(a\)
Build a Büchi automaton that corresponds to it.
Answer: 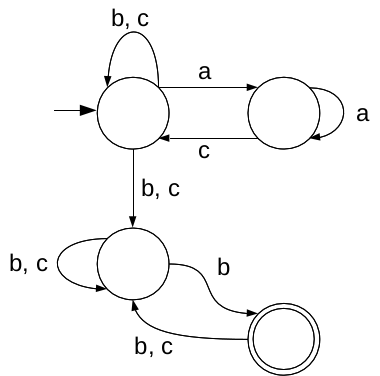
|

 Answer: \((b^{*}a)^{\omega}\)
Answer: \((b^{*}a)^{\omega}\)
 Answer: \((a+b)^{\omega}\)
Answer: \((a+b)^{\omega}\)
 Answer: \((\mathit{authReq}~(\mathit{reject} + \mathit{accept}~\mathit{access}^{*}~\mathit{release}))^{\omega}\)
Answer: \((\mathit{authReq}~(\mathit{reject} + \mathit{accept}~\mathit{access}^{*}~\mathit{release}))^{\omega}\)


