Aritmetik
3.1. Ange decimala motsvarigheten till följande 8-bitars tal givna på binär form.
a) 01010101
b) 00111100
c) 10101010
d) 11000011
a) (01010101)2 = (85)10
b) (00111100)2 = (60)10
c) (10101010)2 = (170)10
d) (11000011)2 = (195)10
3.2 Ange decimala motsvarigheten till följande 8-bitars tal givna på tvåkomplementsform.
a) 01010101
b) 00111100
c) 10101010
d) 11000011
a) (01010101)2 = (85)10
b) (00111100)2 = (60)10
c) (10101010)2 = (-86)10
d) (11000011)2 = (-61)10
3.3 Ange följande decimala tal som 8-bitars binära tal på tvåkomplementsform. (Ledning, bestäm först binär form av talet utan minustecken, tvåkomplementera därefter)
a) -10
b) -38
c) -42
d) -56
a) -10 = -(0000 1010)2 = 1111 01102
b) -38 = -(0010 0110)2 = 1101 10102
c) -42 = -(0010 1010)2 = 1101 01102
d) -56 = -(0011 1000)2 = 1100 10002
3.4 Utför (visa med papper och penna) följande additioner (R=X+Y) av 8-bitars tal givna på binärform. Ange X,Y och R på decimal form, ange dessutom hur flaggorna C och Z påverkas av operationerna.
a) X =
00100100 Y =
01001010
b) X =
10111100 Y =
01000100
c) X =
10000001 Y =
10000001
d) X =
01001010 Y =
00110101
e) X =
01001010 Y =
01001010

Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.

Operationen innebär X=188, Y= 68, R= 0, men 188+68=256 !
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, dessutom blir i detta fall innehållet i registret 0 varför Z-flaggan också sätts till 1.
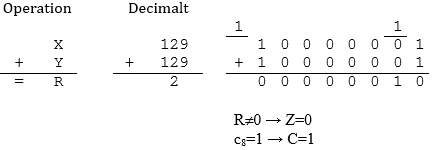
Operationen innebär X=129, Y=129, R=2, men 129+129=258! Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, resultatet i registret är dock skilt från 0 varför Z-flaggan sätts till 0.
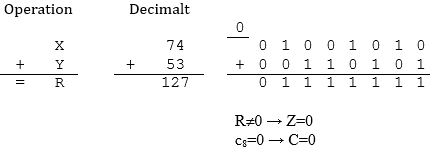
Operationen innebär X=74, Y=53, R=127. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.

Operationen innebär X=74, Y=74, R=148. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
3.5 Utför (visa med papper och penna) följande additioner (R=X+Y) av 8-bitars tal givna på tvåkomplementsform.
Ange X,Y och R på decimal form, ange dessutom hur flaggorna N, V och Z påverkas av operationerna.
a) X =
00100100 Y =
01001010
b) X =
10111100 Y =
01000100
c) X =
10000001 Y =
10000001
d) X =
01001010 Y =
00110101
e) X =
01001010 Y =
01001010

Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.

Operationen innebär X=-68, Y= 68, R= 0,(-68+68=0).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet inom talområdet.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0, dessutom blir i detta fall
innehållet i registret 0 varför Z-flaggan sätts till 1.
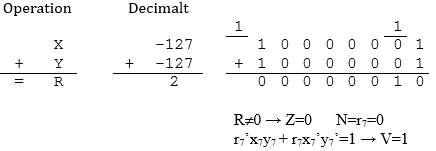
Operationen innebär X=-127, Y=-127, R= 2 men -127-127 = -254.
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och
således resultatet utanför talområdet. Av teckenöverläggningen (två negativa tal adderas men resultatet blir positivt)
ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
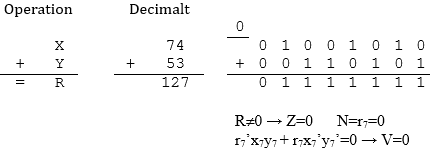
Operationen innebär X=74, Y= 53, R= 127, (74+53=127). Eftersom talen betraktas på tvåkomplementsform
är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.

Operationen innebär X=74, Y=74, R= -108, resultatet är alltså fel.
Talen betraktas på tvåkomplementsform och talområdet (8 bitar) är -128- +127 och således resultatet inom talområdet.
Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi dock att V-flaggan sätts
till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
3.6 Utför (visa med papper och penna) följande subtraktioner (R=X-Y) av 8-bitars tal givna på binärform.
Ange X,Y och R på decimal form, ange dessutom hur flaggorna C och Z påverkas av operationerna.
Flaggan C förutsätts vid denna operation representera en lånesiffra (”borrow”) till den mest signifikanta positionen.
a) X =
01111110 Y =
01010000
b) X =
01010000 Y =
01111110
c) X =
11011110 Y =
00100010
d) X =
00100010 Y =
11011110

Operationen innebär X=126, Y=80, R=46.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.

Operationen innebär X=80, Y=126, R=210.
Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.

Operationen innebär X=222, Y=34, R=188.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.
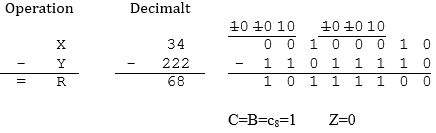
Operationen innebär X=34, Y=222, R=68.
Resultatet är fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.
3.7 Utför (visa med papper och penna) följande subtraktioner (R=X-Y) av 8-bitars tal givna på binärform.
Subtraktionerna ska utföras som addition av 2-komplement, dvs. R = X + (2~Y).
Ange X,Y och R på decimal form, ange dessutom hur flaggorna C och Z påverkas av operationerna.
Eftersom subtraktionen utförs som addition av 2-komplement förutsätts flaggan C vid denna
operation representera inversen av en lånesiffra (”borrow”) till den mest signifikanta positionen.
a) X =
01111110 Y =
01010000
b) X =
01010000 Y =
01111110
c) X =
11011110 Y =
00100010
d) X =
00100010 Y =
11011110
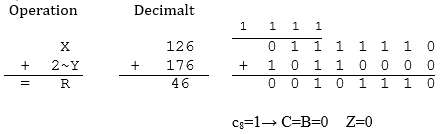
Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=176, R=46 eftersom talen betraktas på binärform med talområdet 0-255 och alltså är resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.

Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=130, R=210. Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
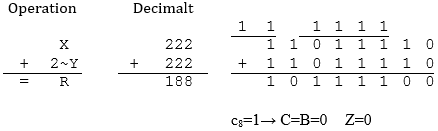
Det gäller att X=222, Y=34, korrekt resultat R=188. Operationen innebär X=222, 2~Y=222, R=188. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.

Det gäller att X=34, Y=222, korrekt resultat R=-188. Operationen innebär X=34, 2~Y=34, R=68. Resultatet är fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
3.8 Utför (visa med papper och penna) följande subtraktioner (R=X-Y) av 8-bitars tal givna på tvåkomplementsform.
Subtraktionerna ska utföras som addition av 2-komplement, dvs. R = X + (2~Y).
Ange X,Y och R på decimal form, ange dessutom hur flaggorna N, V och Z påverkas av operationerna.
a) X =
01111110 Y =
01010000
b) X =
01010000 Y =
01111110
c) X =
11011110 Y =
00100010
d) X =
00100010 Y =
11011110
e) X =
01000000 Y =
10111111
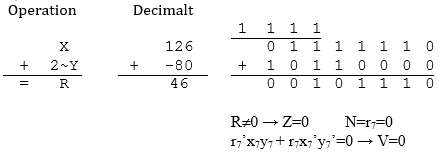
Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=-80, R=46 . Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och operationens resultat korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
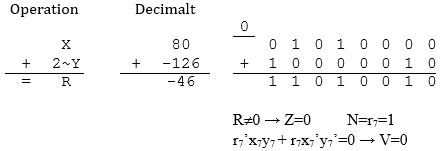
Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=-126, R=-46. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.

Det gäller att X=-34, Y=34, korrekt resultat R=-68. Operationen innebär X=-34, 2~Y=-34, R=-68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
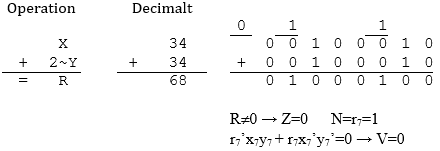
Det gäller att X=34, Y=-34, korrekt resultat R=68. Operationen innebär X=34, 2~Y=34, R=68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.

Det gäller att X=64, Y=-65, korrekt resultat R=129. Operationen innebär X=64, 2~Y=65, R=-127. Operationens resultat är fel. Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
 Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
 Operationen innebär X=188, Y= 68, R= 0, men 188+68=256 !
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, dessutom blir i detta fall innehållet i registret 0 varför Z-flaggan också sätts till 1.
Operationen innebär X=188, Y= 68, R= 0, men 188+68=256 !
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, dessutom blir i detta fall innehållet i registret 0 varför Z-flaggan också sätts till 1.
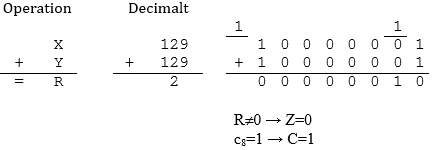 Operationen innebär X=129, Y=129, R=2, men 129+129=258! Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, resultatet i registret är dock skilt från 0 varför Z-flaggan sätts till 0.
Operationen innebär X=129, Y=129, R=2, men 129+129=258! Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet utanför talområdet. Carryflaggan sätts därför till 1, resultatet i registret är dock skilt från 0 varför Z-flaggan sätts till 0.
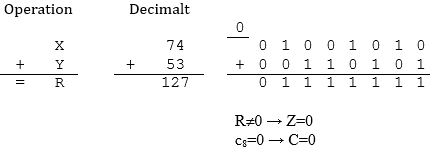 Operationen innebär X=74, Y=53, R=127. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
Operationen innebär X=74, Y=53, R=127. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
 Operationen innebär X=74, Y=74, R=148. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
Operationen innebär X=74, Y=74, R=148. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0.
 Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Operationen innebär X=36, Y= 68, R= 104, (36+68=104).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
 Operationen innebär X=-68, Y= 68, R= 0,(-68+68=0).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet inom talområdet.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0, dessutom blir i detta fall
innehållet i registret 0 varför Z-flaggan sätts till 1.
Operationen innebär X=-68, Y= 68, R= 0,(-68+68=0).
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och således resultatet inom talområdet.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0, dessutom blir i detta fall
innehållet i registret 0 varför Z-flaggan sätts till 1.
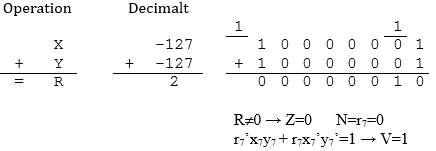 Operationen innebär X=-127, Y=-127, R= 2 men -127-127 = -254.
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och
således resultatet utanför talområdet. Av teckenöverläggningen (två negativa tal adderas men resultatet blir positivt)
ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
Operationen innebär X=-127, Y=-127, R= 2 men -127-127 = -254.
Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och
således resultatet utanför talområdet. Av teckenöverläggningen (två negativa tal adderas men resultatet blir positivt)
ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
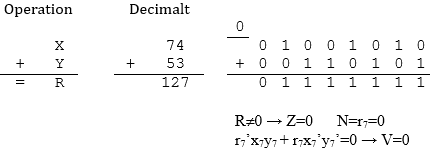 Operationen innebär X=74, Y= 53, R= 127, (74+53=127). Eftersom talen betraktas på tvåkomplementsform
är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Operationen innebär X=74, Y= 53, R= 127, (74+53=127). Eftersom talen betraktas på tvåkomplementsform
är talområdet (8 bitar) -128- +127 och således resultatet korrekt.
Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0.
Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
 Operationen innebär X=74, Y=74, R= -108, resultatet är alltså fel.
Talen betraktas på tvåkomplementsform och talområdet (8 bitar) är -128- +127 och således resultatet inom talområdet.
Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi dock att V-flaggan sätts
till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
Operationen innebär X=74, Y=74, R= -108, resultatet är alltså fel.
Talen betraktas på tvåkomplementsform och talområdet (8 bitar) är -128- +127 och således resultatet inom talområdet.
Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi dock att V-flaggan sätts
till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
 Operationen innebär X=126, Y=80, R=46.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.
Operationen innebär X=126, Y=80, R=46.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.
 Operationen innebär X=80, Y=126, R=210.
Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.
Operationen innebär X=80, Y=126, R=210.
Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.
 Operationen innebär X=222, Y=34, R=188.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.
Operationen innebär X=222, Y=34, R=188.
Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt.
Detta indikeras också av att C-flaggan är 0, dvs. ingen lånesiffra genereras från position c8.
 Operationen innebär X=34, Y=222, R=68.
Resultatet är fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.
Operationen innebär X=34, Y=222, R=68.
Resultatet är fel eftersom negativa tal inte kan representeras av talområdet.
(Eftersom talen betraktas på binärform är talområdet 0-255).
Detta indikeras också av att C-flaggan är 1, dvs. lånesiffra genereras från position c8.
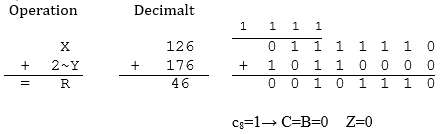 Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=176, R=46 eftersom talen betraktas på binärform med talområdet 0-255 och alltså är resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.
Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=176, R=46 eftersom talen betraktas på binärform med talområdet 0-255 och alltså är resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.
 Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=130, R=210. Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=130, R=210. Resultatet är uppenbarligen fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
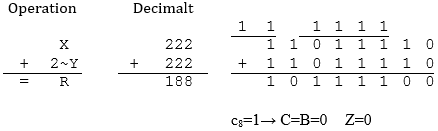 Det gäller att X=222, Y=34, korrekt resultat R=188. Operationen innebär X=222, 2~Y=222, R=188. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.
Det gäller att X=222, Y=34, korrekt resultat R=188. Operationen innebär X=222, 2~Y=222, R=188. Eftersom talen betraktas på binärform är talområdet (8 bitar) 0-255 och således resultatet korrekt. Detta indikeras också av att C-flaggan är 0, dvs. minnessiffran i position c8 är 1.
 Det gäller att X=34, Y=222, korrekt resultat R=-188. Operationen innebär X=34, 2~Y=34, R=68. Resultatet är fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
Det gäller att X=34, Y=222, korrekt resultat R=-188. Operationen innebär X=34, 2~Y=34, R=68. Resultatet är fel eftersom negativa tal inte kan representeras av talområdet. (Eftersom talen betraktas på binärform är talområdet 0-255) . Detta indikeras också av att C-flaggan är 1, dvs. minnessiffran i position c8 är 0.
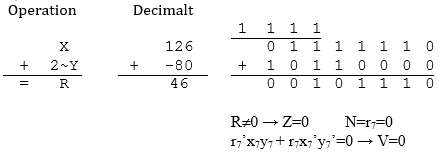 Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=-80, R=46 . Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och operationens resultat korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Det gäller att X=126, Y=80, korrekt resultat R=46. Operationen innebär X=126, 2~Y=-80, R=46 . Eftersom talen betraktas på tvåkomplementsform är talområdet (8 bitar) -128- +127 och operationens resultat korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
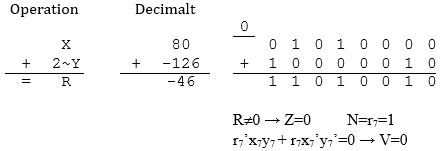 Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=-126, R=-46. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Det gäller att X=80, Y=126, korrekt resultat R=-46. Operationen innebär X=80, 2~Y=-126, R=-46. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
 Det gäller att X=-34, Y=34, korrekt resultat R=-68. Operationen innebär X=-34, 2~Y=-34, R=-68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Det gäller att X=-34, Y=34, korrekt resultat R=-68. Operationen innebär X=-34, 2~Y=-34, R=-68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
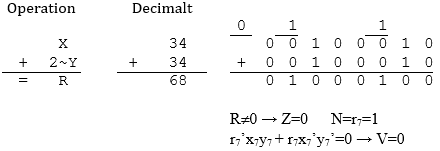 Det gäller att X=34, Y=-34, korrekt resultat R=68. Operationen innebär X=34, 2~Y=34, R=68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
Det gäller att X=34, Y=-34, korrekt resultat R=68. Operationen innebär X=34, 2~Y=34, R=68. Operationens resultat är korrekt. Inget spill alltså och av teckenöverläggningen ser vi hur V-flaggan sätts till 0. Resultatet är skilt från 0 och därmed sätts Z-flaggan till 0.
 Det gäller att X=64, Y=-65, korrekt resultat R=129. Operationen innebär X=64, 2~Y=65, R=-127. Operationens resultat är fel. Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.
Det gäller att X=64, Y=-65, korrekt resultat R=129. Operationen innebär X=64, 2~Y=65, R=-127. Operationens resultat är fel. Av teckenöverläggningen (två positiva tal adderas men resultatet blir negativt) ser vi att V-flaggan sätts till 1 som indikator på spillet. Resultatet är skilt från 0 varför Z-flaggan sätts till 0.