Tillämpad digital signalbehandling

Webintroduktion

Förord

Detta är ett försök att på ett beskrivande och sammanfattande sätt beskriva kursens innehåll. Beskrivningen kommer att hålla sig på en ganska ytlig nivå och går inte in på detaljer, dessa detaljer är dock nödvändiga för att klara av kursen så det här materialet skall inte ses som en ersättning för kursmaterialet utan mer som en sammanfattande introduktion.

Inget större arbete är nedlaggt på själva layouten, den är direktgenererad från Word, och det gör att det dyker upp en del tomma avsnitt i texten i samband med bilder.

Arbete är inte heller nedlagt på att få texten att fungera i olika webläsare.

Texten finns också i en pdf-version (*.pdf) [414 kB] för den som så önskar.

Introduktion

Låt oss börja med att ringa in vårt område och ge exempel på några applikationer.

Vad menar vi med signalbehandling?

Vi ser signalbehandling som ett mycket brett begrepp och det kan i sin enklaste form bara bestå av att vi hanterar en signal utan att på något sätt förändra eller analysera den. I de flesta fall går vi dock längre och kan tänkas analysera signalen och till exempel bestämma dess frekvensinnehåll. Resultatet av denna analys kan sedan bli att vi vill förändra signalen på något sätt. Vi kanske till exempel vill ta bort (filtrera bort) en del frekvenser ur signalen. I båda fallen måste vi kunna göra beräkningar på signalen och då måste vi börja med att hitta sätt att beskriva vår signal och vi måste dessutom kunna beskriva funktionen och egenskaperna hos det signalbehandlingssystem vi använder för analysen eller filtreringen.

Vi kan grovt dela in vår signalbehandling i två delar

· Analys där vi bestämmer någon typ av egenskaper hos en signal eller ett system

· Påverkan där vi på något sätt förändrar en signal eller ett systems egenskaper. Det kan exempelvis röra sig om filtrering av en signal eller kombination av flera delsignaler

Vad innebär det att en signal är digital?

Då vi studerar eller beskriver en signal så har vi två parametrar att ta hänsyn till. Hur skall vi beskriva signalens storlek och hur skall vi beskriva dess tidsförlopp? Båda parametrarna kan vara kontinuerliga eller diskreta. För en kontinuerlig parameter gäller att den kan anta vilket värde som helst medan en diskret parameter bara kan anta diskreta värden. För en digital signal gäller att både tids- och storleksparametrarna är diskreta.

Tidsdiskret signal

För en tidsdiskret sgnal så är det tidsförloppet som är diskretiserat och detta innebär då att vi bara känner till signalens värde vid diskreta tidpunkter. I de flesta fall är dessa tidpunkter jämnt fördelade i tiden, dvs vi känner signalens värde till exempel en gång i timmen, en gång i sekunden, en gång var tionde mikrosekund etc.

Frågan uppkommer då omedelbart: hur ofta måste vi känna signalens värde för att vår värdeserie skall beskriva signalen på ett tillräckligt noggrant sätt? Det kan till exempel inte vara tillräckligt att veta vår bils exakta position var tionde sekund om vi är ute och kör. Då skulle vi nog inte klara av att följa vägen. Är vi däremot ute och går så kanske denna positionsbestämning är tillräcklig.

I de sammanhang som är aktuella i denna kurs så karakteriseras våra signaler bland annat av sitt frekvensinnehåll och vi skall senare se att förutsättningen för att vi skall ha tillräcklig information om vår signal är att tiden mellan två tidpunkter då vi känner signalens värde inte är längre än halva periodtiden hos den signalkomponent som har kortast periodtid. Detta är det samma som att säga att mäthastigheten, den frekvens med vilken vi känner signalens värde skall vara större än dubbla maximala signalfrekvensen. Detta kallas samplingsvillkoret och är ett fundamentalt villkor vid tidsdiskret signalbehandling som vi återkommer till.

Vi sa att signalens värde bara är känd (definierad) vid dessa diskreta tidpunkter men uppfyller vi samplingsvillkoret så kan inte en tidskontinuerlig signal som vi bara studerar vid dessa diskreta tidpunter anta slumpmässiga värden mellan tidpunkterna utan vi kan utifrån dessa tidsdiskreta värden återskapa den tidskontinuerliga signalen.

Amplituddiskret signal

Här gäller då på samma sätt som för tidsförloppet att vi har diskreta värden. Det betyder då att signalens storlek bara kan anges som diskreta värden, vår mätnoggrannhet är inte bättre än så. Även här är dessa nivåer oftast jämnt fördelade. Vi kan till exempel bara ange en temperatur med hela gradtal (jämför en termometer som visar siffror och inte en kvicksilverstapel).

I de flesta fall kan inte signalstorleken vara vad som helst utan det finns ett definitionsområde för signalstorleken och det räcker då att dela upp detta intervall i nivåer. För termometern skulle det säkert räcka med att kunna visa området minus 50 gradet till plus 50 grader om vi vill visa utomhustemperaturen i Göteborg.

Vi skall se lite mer på detta då vi beskriver ett block för att omvandla en signal med kontinuerlig storlek till en signal med diskret storlek, en så kallad analog/digitalomvandlare.

Exempel på applikationsområden

Låt oss se på ett par exempel där digital signalbehandling har fått avgörande betydelse.

Ljud- och bildbehandling

Inom detta område räcker det egentligen att peka på den klara kvaliteétsförbättring som vi alla har upplevt då vi har övergått från att lyssna på musik från repiga vinylskivor och brusiga kassettband där signalen är analogt lagrad till att i stället lyssna till CD-skivor där informationen är digitalt lagrad.

I CD-exemplet har vi inte gjort annat än att översätta den analoga signalen till digital form, vi har alltså inte påverkat signalen mer än så. Ser vi i stället på modern ljudlagring och –överföring via MP3-formatet så är ambitionen en annan. Här är vi ute efter att reducera den mängd information som måste lagras eller överföras så att vi får plats med mer information respektive kan överföra informationen snabbare. I det här fallet måste vi också ge oss på att påverka, manipulera signalen. Detta är ett avancerat förfarande som inte bara bygger på vad som rent tekniskt är möjligt utan det bygger också på kännedom om våra hörselorgan så att vi kan komma fram vilken del av infomationen vi kan plocka bort eller återge med mindre noggrannhet utan att vi för den skull skall uppleva signalen som förvrängd.

I samband med bildbehandling ser vi liknande tankegångar. Hur skall vi till exempel hantera bildinformationen för att få plats med en hel långfilm på en DVD-skiva. Även här använder vi oss av kunskaper om våra sinnesorgan för att veta vad vi kan ta bort eller minimera. I det här fallet tar vi också till andra knep. En film består av en serie stillbilder som visas i snabb följd så att vi upplever rörelse men vi ser då till att som att inte överföra varje bild för sig utan vi överför i stället bara information om vad som har förändrats från föregående bild i följden.

Mobiltelefoni

I modern mobiltelefoni, till exempel GSM, vimlar det av digital signalbehandling. Vi använder på liknande sätt som i MP3 signalbehandling för att reducera den mängd information som måste överföras för att talsignalen skall bli av acceptabel kvalité.

De flesta ha nog också stött på fall då vi kan höra vårt eget tal som ett eko i telefonen. Vi använder då digital signalbehandling för att släcka ut detta eko. Eftersom vi får en ny uppkoppling varje gång vi ringer ett samtal så är inte förhållandena likadana varje gång utan denna signalbehandling måste anpassa sig till de aktiuella förhållandena, vi säger att signalbehandlingen är adaptiv.

Överföringsförhållandena ändras alltså mellan varje samtal och även under samtalets gång, speciellt om vi rör oss, och det gör att vi hela tiden använder digitala signalbehandlingsmetoder för att få en så effektiv signalöverföring som möjligt.

Vi behöver också metoder för att byta basstation då vi förflyttar oss från en stations täckningsområde till en annan stations täckningsområde. Dessa metoder bygger då bland annat på mätning av signalstyrka.

Egenskaper hos tidsdiskret signalbehandling

Vi har nu tittat på några grundbegrepp runt digital signalbehandling. Även om denna tar över allt större del av signalbehandlingsmarknaden så lever dock analog signalbehandling kvar och det finns mer än historiska skäl till detta. Båda sfärerna har sina förtjänster och vi kan se lite på för- och nackdelarna hos digital signalbehandling.

Positiva egenskaper

Digital signalbehandling sker i form av matematiska beräkningar i en dator eller någon annan form av krets och inte som elektroniska förlopp i komponenter som motstånd och kondensatorer.. Detta gör att vi vet noggrannheten hos våra beräkningar. Att behandlingen sker som en beräkning gör också att vi får samma resultat gång efter gång och i två olika utrustningar som gör samma operation. Vi är alltså inte beroende av toleranser hos komponentvärden eller förändringar på grund av till exempel ändrade temperatur- eller fuktförhållanden.

Vad vi har sagt innebär också att vi har små behov att trimma in vår utrustning efter dessa toleranser eller miljöförändringar.

Digitala system ger ofta stora möjligheter till att integrera vår apparatur i enkla elektroniska kapslar och därmed minska deras storlek.

I många fall sker vår signalbehandling i form av ett beräkningsprogram i någon form av dator. Detta gör att det är lätt att byta funktion hos vår signalbehandling. Vi kan enkelt förändra enstaka parametrar i förloppet eller helt byta program och få en helt annan funktion. Flexibiliteten är alltså mycket större än i analoga system där vi kanske kan påverka enstaka parametrar men inte kan byta funktion utan omkonstruktion eller byte av funktionsblock.

Vi skall senare se att tidsdiskret signalbehandling ger oss möjligheter till förlopp som är omöjliga eller mycket svåra att realisera på analogt sätt. Det gäller till exempel de metoder för informationsreducering som vi ovan nämnde i samband med exemplen på ljud- och bildbehandling.

Vi skall inte heller bortse från att en mycket stor del av våra moderna lagrings- och överföringsmetoder för signaler i sig är digitala och då ’kostar’ det kanske inte mer än några extra rader programkod att samtidigt göra någon önskad manipulering av signalen.

Negativa egenskaper

Vi nämnde ovan att lite signalbehandling kanske bara kostar några rader programkod men detta förutsätter då att vi har andra skäl att ha en digital signal. I många fall är våra signaler från början analoga och vi vill att de fortfarande skall vara analoga efter vår signalbehandling. Har vi nu inga direkta skäl till att i mellanledet göra signalen digital så kommer vi att drabbas av ganska stora initialkostnader. Vi måste ha funktioner för att omvandla den analoga signalen till digital form före signalbehandlingen, vi måste ha funktioner för att göra signalbehandlingen (oftast en dator eller någon form av logisk krets) samt funktioner för att återskapa den analoga signalen efter signalbehandlingen. Det finns många fall där denna investering inte är motiverad.

I praktiken visar det sig också att analoga funktioner är användbara mycket högre upp i frekvens än vad digitala funktioner är. Det betyder till exempel att vi i de flesta fall måste använda analog signalbehandling i sista sändarsteget och första mottagarsteget i in radio- eller telefoniöverföring.

Alla funktioner för digital signal signalbehandling arbetar i grunden med binära signaler. Våra signaler representeras alltså av ett antal ettor och nollor och antalet ettor och nollor i ett värde måste med nödvändighet vara begränsat. Detta gör att antalet steg hos vår amplituddiskreta signal blir begränsat och därmed begränsas noggrannheten i våra beräkningar. I många system är antalet bitar begränsat till 8 eller 16 stycken vilket ger 256 respektive 65536 möjliga amplitudnivåer. Det senare kan låta som mer än tillräckligt men våra beräkningar ger i de flesta fall avrundningsfel som gör att antalet sanna bitar och därmed antalet nivåer blir färre.

Grunder

Låt oss se på ett antal grundbegrepp som gäller de flesta av våra digitala system för att sedan kommentera de olika blocken i systemet.

Typiskt system

Vi börjar med att se på ett typiskt system för att ta hand om en analog signal, göra om denna till digital form, utföra någon form av digital signalbehandling på signalen och sedan återskapa den analoga signalen.

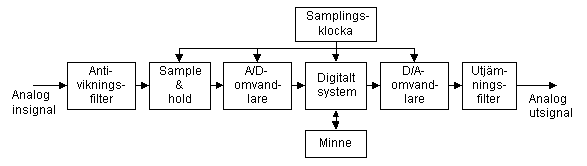
Figuren beskriver ett komplett system. I en del fall kan vi tänka oss att plocka bort delar. Vill vi analysera den analoga signalen så kan det räcka med att ta in signalen i det digitala systemet, göra våra beräkningar och presentera resultatet. Vi har alltså i detta fall ingen anledning att återskapa den analoga signalen och de två sista blocken i kedjan kan utelämnas.

I andra fall, till exempel i en synt, så kan det vara så att vi skapar signalen på digital väg och vill omvandla den till en analog signal. I det fallet börjar signalen sitt liv i den digitala världen och de tre första blocken i figuren kan utelämnas.

Antivikningsfilter

Vi nämnde tidigare samplingsvillkoret, dvs att samplingsfrekvensen måste vara högre än dubbla maximala signalfrekvensen. Uppfylls inte detta så får vi så kallad vikningsdistorsion (aliasing) vilket innebär att frekvenser över halva samplingsfrekvensen kommer att tolkas som om de hade frekvenser lägre än halva samplingsfrekvensen. Inträffar detta så finns det i det flesta fall ingen möjlighet att återställa signalen. Vi måste alltså undvika detta och det gör vi genom att placera ett filter på systemets ingång och detta filter får då bara släppa igenom signaler med frekvenser lägre än halva samplingsfrekvensen.

Sample and hold

Den analoga signalen skall omvandlas till sin digitala motsvarighet. Vi diskretiserar då först tiden genom att ta mätvärden med jämna tidsintervall, vi samplar signalen. Den efterföljande analog/digitalomvandlaren behöver viss tid på sig för att göra omvandlingen och under denna tid bör vi hålla signalstorleken konstant. Sammantaget har vi alltså en så kallad samle and holdfunktion (S/H).

Analog/digitalomvandlare

Analog/digitalomvandlaren (A/D-omvandlare) skall omvandla den analoga signalens (samplade) värde till ett digitalt ord, dvs ett antal binära bitar. Vanlig logik säger att vi med hjälp av B stycken binära bitar kan beskriva olika nivåer och vi delar alltså in vårt arbetsområde i nivåer. Detta gör då att vi kan särskilja nivåförändringar som är större än eller lika med . Vi säger att vi har upplösningen Vi nämnde tidigare att enklare system ofta jobbar med 8 eller 16 bitar vilket ger 256 respektive 65536 nivåer. Det är ganska vanligt att A/D-omvandlare har arbetsområdet volt och detta ger då upplösningen 39 mV respektive 153 mV.

Det största felet vi kan göra i en omvandling är ett halvt steg och vi talar om systemets signal/kvantiseringsbrusförhållande (SQNR) som ofta beräknas i decibel. Vi får ungefär

som i 8 bitars fallet ger 48 dB och i 16 bitars fallet 96 dB.

Digitalt system

I centrum av vårt system ligger det digitala systemet som utför vår signalbehandlingsrutin, till exempel filtrering eller signalanalys. Detta system består av någon form av mikroprocessor eller också är det uppbyggt i hårdvara. I det första fallet brukar man skilja på generella processorer som inte är direkt avsedda för signalbehandling och signalprocessorer som har funktionalitet som är direkt anpassad för signalbehandling. I hårdvarufallet brukar vi skilja på dedikerad elektronik som då är en färdig konstruktion som har skapats i en integrerad krets, oftast en så kallad ASIC-krets (Application Specific Integrated Circuit), och omprogrammerbar elektronik i så kallade FPGA-kretsar (Field Programmable Gate Array).

Minne

Ett signalbehandlingssystem är knappast komplett utan ett minne. Detta behövs för att mellanlagra beräkningsvärden och handlar det om att spela in ett förlopp, till exempel underlaget för en CD, så måste vi ha kapacitet för att lagra denna information. Använder vi en dator för signalbehandlingen så behöver vi dessutom minnesplats för att lagra det signalbehandlingsprogram som körs.

Digital/analogomvandlare

Efter signalbehandlingen vill vi återskapa den analoga signalen och detta sker via en digital/analogomvandlare (D/A-omvandlare). Denna fungerar i princip omvänt mot A/D-omvandlaren, dvs den omvandlar de binära orden till nivåer. Det är värt att lägga märke till att det antal binära bitar vi använder begränsar antalet möjliga nivåer på samma sätt som hos A/D-omvandlaren. Den analoga utsignalen kan altså inte anta vilken nivå som helst.

Utjämningsfilter

Att den analoga utsignalen från D/A-omvandlaren bara kan anta ett antal diskreta nivåer (trappsteg) gör att den genererade analoga signalen kommer att vara uppbyggd som en trappstegsformad signal.

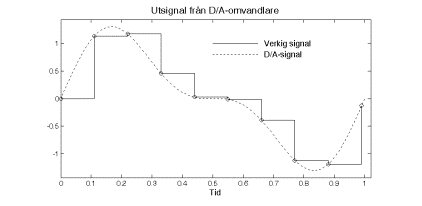
Vi använder ett utjämningsfilter för att ta bort dessa trappsteg. Trappstegen kommer att uppträda i takt med samplingsfrekvensen, dvs stegen i sig innehåller signaler med samplingsfrekvensen och multiplar av denna. Vi minns från samplingen att den behandlade signalen bara får innehålla frekenser lägre än halva samplingsfrekvensen och vi inför då ett utjämningsfilter som bara släpper igenom dessa lägre frekvenser. Vi kan använda samma typ av filter som vi använde som antivikningsfilter.

Det är värt att lägga märke till att både antiviknings- och utjämningsfiltret används på analoga signaler, dvs de måste vara analoga filter och inte digitala filter. Med hjälp av så kallad översampling kan vi dock förenkla den analoga filtreringen och i stället göra delar av denna digitalt.

Talrepresentation

För att kunna bedöma vilka resultat man får i digitala sammanhang så är det viktigt att veta vilken talrepresentation som används i datorn eller hårdvaran. De stora huvudgrupperna är heltal och decimaltal. I signalbehandlingssammanhang är decimaltal vanligast och här kan vi särskilja två huvudtyper, flyttal och fixtal, som i sin tur har sina underavdelningar.

Flyttal

Här beskrivs våra tal som . Har vi stor exponent så kan vi med denna metod representation ett mycket stort talområde. Representationen leder dock till stora och långsamma konstruktioner.

Fixtal

Vid fixtalsrepresentation så är decimalpunktens placering fast, dvs vi har alltid lika många heltals- och decimalsiffror i våra tal. En vanlig variant av fixtal är fraktionella tal där talens belopp alltid måste vara mindre än eller lika med ett, vi har då en teckenbit och ett antal decimaler

Sampling, vikning

Vi har tidigare sagt att vi i tidsdiskreta system normalt sett måste uppfylla samplingsvillkoret, dvs att den maximala signalfrekvensen inte får vara högre än halva samplingsfrekvensen. Uppfyller vi inte detta så kommer vi att få så kallad vikningsdistorsion där signaler med frekvenser över halva samplingsfrekvensen kommer att ’vikas ner’ och uppfattas som om de har frekvenser lägre än halva samplingsfrekvenser. En signal med frekvensen i intervallet halva samplingsfrekvensen till samplingsfrekvensen kommer att tolkas som om den hade frekvensen . Detta får den märkliga effekten att då vi höjer frekvensen hos en signal i detta frekvensintervall så kommer det att uppfattas som om frekvensen sjönk och tvärt om.

Typiska systemdata

Låt oss se på data för några system som är välkända från kommunikationsvärlden.

applikation	samplingsfrekvens	ordlängd
Telefoni/GSM	8 kHz	8 bitar
CD	44,1 kHz	16 bitar
Digital bandspelare, DAT	48 kHz	16 bitar
Bättre ljudkort	44,1/48 kHz	20 bitar
Avancerad studio	96 kHz	24 bitar
Digital radio, DAB	48 kHz	18 bitar

Implementering

För att våra signalbehandlingsrutiner skall göra någon nytta så måste de implementeras i någon form av system. Låt oss se på ett antal alternativ.

Persondator

Vanliga persondatorer används rätt ofta i signalbehandlingssammanhang, speciellt då vi använder program för att editera våra signaler, till exempel program för musikredigering. Dessa system blir ofta flexibla eftersom vi kan få en effektiv miljö i någon grafisk miljö som Windows eller Linux. Persondatorer är dock inte anpassade för denna verksamet och signalbehandlingen blir inte optimal. Vi skall dock inte förakta att vi här har ett färdigt system som eventuellt behöver kompletteras med ett bra instickskort för att samla in och skicka ut signaler. Systemet kan ju också användas för en mängd andra applikationer.

Mikrodatorer

I många typer av inbyggda system finns redan en mikroprocessor och det är då vanligt att använda denna även för signalbehandlingsuppgifter. Vi har även här ett system som inte är optimerat för signalbehandling men det leder ju till att vi kan använda samma processor för flera uppgifter. En del moderna mikroprocessorer har dock fått nya kommandon som är anpassade för signalebehandling, dettta beror på att multimedia med olika typer av signalbehandling ofta är en integrerad del av moderna datorapplikationer.

Signalprocessor

En signalprocessor är en typ av mikroprocessor som är speciellt anpassad för att utföra signalbehandlingsrutiner. Den har alltså fått en kommandouppsättning och struktur som lämpar sig för just detta, samtidigt har då kanske en del andra funktioner som finns i andra processorer men som inte behövs eller är så viktiga för just signalbehandling fått stryka på foten.

Hårdvara

Även om en del moderna processorer har klockfrekvenser upp i gigahertzområdet så tar varje beräkningsoperation ofta ett antal klockcykler och det gör att beräkningshastigheten är för låg för användning i system som arbetar upp emot radiofrekvens. Här blir då i stället hårdvarulösningar intressanta. Vi realiserar alltså våra signalbehandlingsrutiner, inte i form av datorprogram utan i form av elektronik i hårdvara. Vi kan här identifiera två huvudgrupper, dedikerad elektronik (ASIC) där den elektroniska funktionen är fast uppbyggd i en elektronisk krets och programmerbar logik (FPGA) där vi kan byta funktion hos elektroniken. Båda varianterna kan ge mycket snabba lösningar men den första varianten är naturligtvis snabbast eftersom vi här kan optimera elektroniken exakt efter den uppgift som skall utföras, vi skall ju aldrig byta funktion. Denna lösning blir dock mycket dyr om inte kostnaden kan spridas ut över ett stort antal kretsar. Den kan alltså bara bli aktuell då vi är ute efter att massproducera utrustning.

Hur beskriva signaler och system?

Vi har nu berört de komponenter som kan ingå i våra digitala system och ordat lite om analoga och digitala sgnaler. Hur skall vi nu hitta ett språk för att beskriva våra signaler och system? Beskrivningen bör vara så utformad att vi kan använda den för att hantera våra signaler och system på önskat sätt och det leder till att vi får hitta ett matematiskt beskrivningssätt.

I det analoga planet kan vi identifiera tre olika viktiga metoder att göra våra beskrivningar. Vi har ett tidsplan där vi kan beskriva våra signaler som tidsförlopp medan system analyseras med hjälp av differntialekvationer. Denna bskrivning är dock inte så lämplig om vi vill studera en signals frekvensinnehåll eller ett systems frekvensegenskaper utan vi får då övergå till det så kallade frekvensplanet där vi använder frekvensparametern .i våra beskrivningar. Vill vi i stället studera ett systems dynamiska egenskaper, till exempel dess stabilitet så får vi generalisera frekvensplanet och övergå till Laplaceplanet (s-planet).

På motsvarande sätt kan vi beskriva våra digitala signaler och system i tre olika plan. Vi har ett tidsplan där signaler beskrivs som tidsdiskreta tidsförlopp medan system beskrivs av differensekvationer. Vi har ett tidsdiskret frekvensplan som motsvarar det analoga frekvensplanet om vi håller oss till frekvenser under halva signalfrekvensen, vi skall dock se att vi kommer att få ett upprepande frekvensspektra om vi fortsätter uppåt i frekvens. En följd av detta är att vi i vår analys egentligen inte är intresserade av absoluta frekvenser utan i stället av förhållandet mellan aktuella frekvenser och samplingsfrekvensen. Även här kan vi generalisera frekvensplanet och får då det så kallade z-planet. Precis som för analoga signaler så illustrerar de tre planen olika egnskaper hos våra signaler och system och de är inte alternativa plan utan de ger via sina olika egenskaper utökad information om våra signaler och system och ger också olika verktyg att behandla signalerna och systemen.

I den efterföljande texten så skall vi titta lite närmare på de tre planen och först se vilken information de kan ge om våra signaler och system, vi kommer att analysera signaler och system. Vi kommer sedan att övergå till att beskriva metoder för att behandla sigalerna, vi kommer att bygga upp system för vår signalbehandling. I de flesta beskrivningar vi gör så kommer vi att skapa olika former av filter. Detta är dock bara en delmängd av vår totala signalbehandlingsarsenal.

I den grundläggande analysen och syntesen så kommer vi att betrakta signaler och system som tidsdiskreta, vi kommer dock inte att ta hänsyn till den begränsade noggrannhet som vår begränsade ordlängd ger upphov till utan det gör vi efteråt. Detta gör att det då kanske inte är möjligt att realisera önskade funktioner med målsystemets ordlängd och vi får göra kompromisser i vår realisering.

Tidsplanet

Vi minns från analoga bskrivningar att signaler och system brukar beskrivas av tidsfunktioner som respektive . Vi behöver motsvarande beskrivningar. Vi har tidigare sagt att vi här har samplade signaler och system där deras värden bara är kända vid diskreta tidpunkter givna av samplingsfrekvensen, låt oss kalla denna frekvens för . Tiden mellan två tidpunkter där våra signaler är definierade ges då av , där är vår samplingsperiod. Resonemanget gör att vi kan beskriva tidsförloppen som funktioner med en uppräknande tidsvariabel. Vi kan beskriva en signal som , där då är ett heltal . Eftersom samplingsperioden alltid kommer att ingå i våra tidsdiskreta uttryck så utelämnar vi denna och skriver i stället förkortat . Lägg märke till att vi använder hakparenteser runt vår variabel i uttrycket för den tidsdiskreta signalen medan vi använde vanliga parenteser i det tidskontinuerliga fallet. I fortsättningen kommer vi att använda vanliga parenteser för kontinuerliga förlopp och hakparenteser för diskreta förlopp oberoende av aom vi är i tids- eller frekvensplanet.

Värdet på variabeln avgör vi till stor del själva, det är inte fråga om absolut tid. Vi de flesta fall sätter vi tiden till noll, dvs , vid den tidpunkt då vi börjar betrakta vår signal eller vårt system.

Enkla signaler

För att studera egenskaper hos våra system så kan det bra att ha några enkla signaler att tillgå. Vi kan också använda dessa grundelement för att bygga upp mer komplicerade uttryck. Vi skall se på några sådana enkla signaler.

Den enklaste signalen kallas för en impuls och betecknas . Denna signal har egenskapen att ha värdet ett vid tidpunkten noll medan den är noll vid alla andra tidpunkter. Impulsen kan användas för att bygga upp alla andra tidsdiskreta signaler. Den används också som testsignal. Om vi skickar in denna signal i ett system som kommer utsignalen att bli det så kallade impulssvaret. Denna utsignal visar då hur systemet reagerar på en kortvarig störning på ingången och säger en hel del om ett systems dynamiska egenskaper.

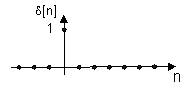
En annan enkel signal är ett steg eller enhetsteg som betecknas . Denna signal har egenskapen att den är noll för alla tidpunkter före tidpunkten noll för att sedan från och med denna tidpunkt vara ett. I praktiken kan en signal inte vara ett in i tidens oändlighet, men den är i alla fall ett så länge som vi betraktar vårt system.

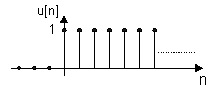
Även denna signal används som testsignal, vi får det så kallade stegsvaret och detta beskriver då hur ett system reagerar då vi plötsligt ändrar insignalen, till exempel hur temperaturen ändras då vi ändrar önskad temperatur i ett klimatsystem från 20 till 15 °C.

En annan enkel signal som inte är lika ofta använd är rampen. Denna betecknas och är noll för negativa tider för att sedan vara lika med från och med tiden noll.

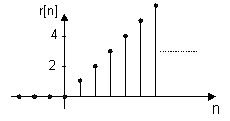
En grundläggande men inte lika enkel signal är sinusfunktionen som inte har någon egen beteckning men som beskrivs av uttrycket

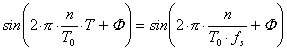
Där är signalens periodtid. Tiden är inte nödvändigtvis ett heltal, vi återkommer strax till detta i samband med periodiska signaler. är signalens fasförskjutning och faktorn gör att vi kan representera sinusformade signaler med alla olika faslägen, till exempel cosinussignaler.

Vi har nu sett på några grunsfunktioner. Hur gör vi nu om vi om vi vill ha någon av grundfunktionerna men vi vill ha en annan storlek på signalen eller om vi vill att signalen skall ligga vid en annan tidpunkt?

Att ändra signalens storlek är lätt det är bara att multiplicera den med en konstant av önskad storlek, grundfunktionerna har i sig storleken ett. Vi beskriver alltså en impuls med storleken 2,5 som . Med en negativ konstant kan vi också göra vår signal negativ.

För att förflytta en signal i tid så inför vi uttrycket som gör att signalen förslyttas steg i tid. Ett positivt värde på gör att signalen fördröjs medan ett negativt värde gör att signalen tidigareläggs. Signalen är då en signal som är noll för tider fram till tiden , där den får storleken –3,6 och den kommer sedan att ligga kvar med denna storlek vid efterföljande tider.

Periodisk signal

I signalsammanahang talar vi om periodiska oxh aperiodiska signaler.

En periodisk signal har ett upprepande förlopp, dvs då vi låter tiden gå så kommer vi med jämna intervall att återfå en signal med samma tidsförlopp och tiden för ett uuprepande förlopp är då signalens periodtid. Vi kan identifiera två varianter. En periodisk signal i största allmänhet har en kurvform som ser lika dan ut i varje period den behöver däremot inte ha samplingspunkterna på samma ställen i olika perioder. En strikt periodisk signal utmärks av att samplingspunkterna och därmed samplingsvärdena är de samma i varje period, vi får till exempel en strikt periodisk sinussignal om i ovanstående uttryck kan uttryckas som ett bråk.

En aperiodisk signal å andra sidan har inget upprepande förlopp. Ett exempel kan vara en vanlig talsignal.

Linjärt, tidsinvariant

All grundläggande signalbehandling bygger på att signaler och system är linjära och tidsinvarianta. Vad betyder då det?

Ett system är linjärt om vi kan tillämpa superposition, dvs om en gånger så stor insignal bara ger den förändringen att utsignalen också blir gånger så stor. Den skall dessutom ha egenskapen att består insignalen av en summa av flera insignaler så kan vi få fram den totala utsignalen genom att beräkna eller mäta utsignalen för varje insignal och sedan addera ihop dessa utsignaler till den totala utsignalen. Ett typiskt fall då linjaritet inte längre gäller är då vi har för stor insignal så att vårt system bottnar.

Ett system är tidsinvariant om det inte spelar någon roll när i tiden vi applicerar en insignal. Gör vi det lite senare i tid så skall enda förändringen bli att utsignalen kommer lika mycket senare. Utsignalens utseende skall inte förändras.

Signalbeskrivning

Vi såg tidigare på ett antal enkla grundsignaler och vi kan använda och kombinera dessa för att beskriva mer komplicerade signaler. Det är till exeempel alltid möjligt att beskriva en signal som en följd av tidsskiftade och skalade impulser enligt

eller rent generellt

där en del konstanter kan vara noll.

Differensekvation

Låt oss se hur vi kan beskriva våra tidsdiskreta system i form av en differensekvation.

Grundoperationer, addition, tidsskift, skalning

Vi kan visa att för linjära, tidsinvarianta system så klarar vi oss med tre grundoperationer för att beskriva våra system, dessa är

· summation för att summera delsignaler. Observera att vi för linjära system inte kan addera en konstant till våra signaler utan det måste vara en summation av signaler

· skalning, dvs multiplikation av (del)signalen med en konstant

· tidsskift, dvs tidsförskjutning av signalen

Vi kan också behöva subtraktion men vi löser då denna som multiplikation med en negativ konstant och summation.

Vi kommer att få uttryck av typen

Vi ser att utsignalen () byggs upp av tidsskiftade in- och utsignaler. Vad gäller insignalen så ser vi att kan ha nuvarande insignal (), tidigare insignaler () och kommande insignaler ().

Vad gäller utsignalen kan vi bara ha med tidigare utsignler(). Vi håller ju på att bygga upp nuvarande utsignal så den kan inte gärna vara med och det faller lite på sin orimlighet att vi skulle ha med kommande utsignaler.

Kausalitet

Vi såg ovan hur vår differensekvation kan innehålla tidigare, nuvarande och framtida insignale. I ett realtidssystem, dvs ett system där vi fortlöpande samlar in insignaler och genererar nya utsignaler så kan vi inte gärna känna till framtida insignaler och dessa får inte vara med i ett sådant system. Ett system där differensekvationen bara innehåller nuvarande och tidigare insignaler samt tidigare utsignaler kallas för ett kausalt system och är mycket viktigt då realtidssystem är vanligt förekommande.

Transversellt, rekursivt

Vi kan även göra en annan indelning i två olika typer av system. Har vi ett system som bara innehåller nuvarande och tidigare insignaler men inga tidigare utsignaler så kallas detta för ett transversellt system. Då systemekvationen inte använder sig av systemets utsignaler så finns det ingen återkoppling i systemet och detta leder till att ett sådant system aldrig kan bli instabilt. Ett sådant system kallas också för ett FIR-system (Finite Impulse Response). Vi skall senare se vad detta namn innebär.

Innehåller vårt system tidigare utsignaler, dvs systemet har återkoppling så kallas detta för ett rekursivt system och återkopplingen gör då att en felaktig dimensionering eller begränsad ordlängd kan göra systemet instabilt. Sådana system kallas också för IIR-system (Infinite Impulse Response), även detta återkommer vi till.

Orsaken till att rekursiva system förekommer trots risken för instabilitet är att dessa system kan dimensioneras för att påverka våra signaler mycket kraftigare än vad transversella system kan göra. En annan egenskap hos transversella system som ofta är eftersträvansvärd är att dessa system kan dimensioneras för linjär fas, även detta är något vi återkommer till.

Blockschema

Man brukar säga att en bild säger mera än tusen ord och det gör att det är lättare att få grepp över ett systems struktur om vi ritar vår differensekvation som ett blockschema. Detta schema är då uppbyggt av symboler för våra grundelement i deifferensekvationen, dvs summation, skalning och tidskift.

Vi kan till exempel rita differensekvationen

som blockschemat

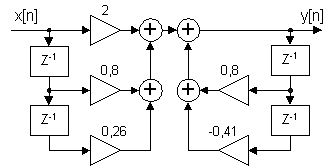
I praktiken kan man bara rita vettiga blockscheman för kausala system. Det är värt att komma ihåg att blockschemat bara är en bild av vårt system och inte beskriver dess fysiska uppbyggnad. Differensekvationen realiseras ju i de flesta fall som några rader i ett dataprogram.

Systemegenskaper

För att kunna dimensioera våra digitala system så räcker det inte med dimensioneringsregler. Vi måste också ha metoder för att analysera systemets egenskaper. Vi kan identifiera och tolka olika egenskaper i våra tre olika tidsdiskreta plan (tidsplan, frekvensplan och z-plan). Låt oss för tillfället koncentrera oss på tidplanet.

Impulssvar

Då vi beskrev impulsen som en grundsignal så nämnde vi att den kan användas för att testa hur ett system reagerar på en kort störning och att vi då får det så kallade impulssvaret. Vi får då detta genom att beräkna systemets utsignal om systemet har insignalen . Vi kan naturligtvis även mäta på färdiga system genom att mäta utsignalen om systemet får denna insignal. Vad vi här kan vänta oss är att systemmet efter en tid återgår till viloläget

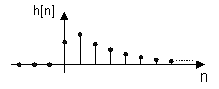
Ibland får vi en insvängning runt viloläget innan systemet återgår till vila

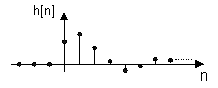
Metoden är inte begränsad till tidsdidkreta system utan är lika vanlig för tidskontinuerliga system, den är till exempel vanlig då vi i akustiska sammanhang vill mäta ett rums efterklangstid, dvs den tid det tar för en signal att dö ut i det aktuella rummet. Efterklangstiden är defenierad som den tid som det tar för ljudet från en impuls att sjunka med 60 dB.

Stegsvar

Vi sa också tidigare att ett steg är en annan användbar testsignal. Vi är i det fallet ute efter att bestämma hur systemet reagerar på en kvarstående förändring av insignalen och vi har insignalen . Det vi är kan vänta oss brukar vara en stegvis övergång till den nya utsignalen

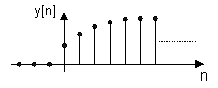
eller också en insvängning mot det nya värdet innan resulatet stabiliserar sig

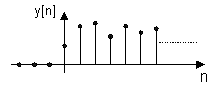
Stabilitet

Vi sa nyss att impulsvsaret efter en tid bör återgå till vilotillståndet, dvs tillståndet vi hade före störningen medan stegsvaret övergår till sin nya utsignal. Inträffar inte detta utan vi får en kvarstående svängning eller en signal som mer eller minde snabbt växer och går mot bottning så har vi ett instabilt system, vilket inte är önskvärt.

Analys av ett enkelt system

Låt oss se hur ett mycket enkelt system kan uppföra sig. Det enklasts system vi kan tänka oss är förmodligen ett system som bara adderar nuvarande sampel till föregående sampel, dvs

De två samplen är tidsfördröjda i förhållande till varandra. Oberoende av signalfrekvens är denna tid lika med samplingsperioden . Låt oss fundera på vad som händer då vi har olika signalfrekvenser. Vid låg frekvens är fördröjningen kort i förhållande till signalens periodtid och de två summerade signalerna ligger i stort sett i fas, dvs de samverkar och ger ungefär dubbel amplitud. Då vi höjer signalfrekvensen så kommer fördröjningen att bli en allt större del av signalperioden och de två delsignalerna kommer allt mer i ofas, dvs de kommer inte längre att samverka så väl. Så småningom så kommer fördröjningen att bli lika med halva periodtiden hos signalen och de två delsignalerna hamnar i motfas och släcker ut varandra. Detta inträffar när signalfrekvensen är lika med halva samplingsfrekvensen. Fortsätter vi att höja signalfrekvensen, trots att vi då bryter mot samlingsvillkoret, så kommer de två delsignalerna att börja bli i fas igen och då vi når upp till att signalfrekvens och samplingsfrekvens sammanfaller så är den ena signalen precis en period fördröjd och de två delsignalerna ligger i fas igen. Vi får alltså samma förhållande som vid likspänning. Vi kan konstatera att spektrat upprepar sig, speglar sig då vi kommer över halva samplingsfrekvensen. Sammanfattningsvis så har vi i det tillåtna frekvensområdet upp till halva samplingsfrekvensen ett lågpassfilter, dvs ett filter som släpper igenom låga frekvenser bättre än höga frekvenser.

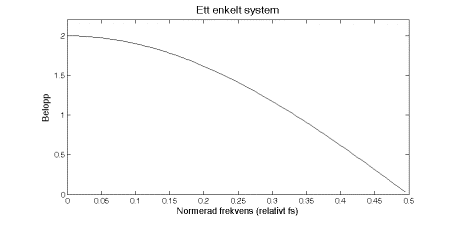
Vårt lilla resonemang gör det uppenbart att vi får ett frekvensberoende hos systemet och skulle vi bygga ut systemet med fler delsignaler med olika antal stegs fördröjning och lägga till fördröjda, återkopplade utsignaler samt skala de olika termerna med olika (positiva eller negativa) konstanter så skulle möjligheterna att styra frekvenseberoendet öka. Vi skall senare finna metoder för att göra detta.

Utsignal från insignal

Vi har sett hur vi kan använda speciella testsignaler för att studera våra systems egenskaper. När vi sedan skall använda vårt system praktiskt så får vi ersätta testsignalen med den verkliga insignalen och på samma sätt beräkna vår utsignal steg för steg. Har vi ett realtidssystem där vi hela tiden hämtar in insignaler och genererar utsignaler så leder i de flesta fall varje nytt värde hos insignalen till beräkning av ett nytt värde hos utsignalen. Det förekommer också att beräkningen sker i block av sampel.

Faltning

I detta sammanhang talar vi om faltning, ett begrepp som brukar ses som svårbegripligt och ser man bara definitionsekvationen

så är det väl så. Vi ser att ekvationen innehåller insignalen och systemets impulssvar och vad vi gör är helt enkelt att betrakta insignalen som en serie av skalade och tidsskiftade impulser som var och en ger upphov till motsvarande skalade och tidsskiftade impulssvar och enligt superpositionsprincipen så kan vi beräkna den totala utsignalen genom att tidpunkt för tidpunkt summera ihop de olika impulssvaren.

I de flesta fall kan vi lika gärna undvika detta betraktelsesätt och i stället bara använda vår differensekvation för att beräkna utsignalen tidpunkt för tidpunkt.

Det kan dock förekomma fall då vi inte känner ett systems differensekvation utan vi har bara mätt upp systemets impulssvar och då kan metoden vara användbar. Exempel på detta är att det på senare tid har kommit ett antal högkvalitativa reverbenheter (efterklang) för musik där man har uppmätt impulssvaret (efterklangen) i ett antal erkänt bra konsertlokaler och använder detta impulssvar för att via faltning ge den inspelade musiken efterklang.

Det kan vara värt att lägga märke till att det inte finns något som hindrar oss från att betrakta impulssvaret som en transversell differensekvation och behandla den som en sådan. Ett impulssvar behöver dock inte ha ändlig längd, det kan i princip pågå hur länge som helst även om det måste gå mot noll och då så småningom försvinner i vår ordlängds upplösning. Vi kan inse att om vi i ovanstående exempel har en konsertlokal med flera sekunders efterklangstid så blir antalet beräkningar för varje nytt utvärde mycket stort.

Seriekoppling

Ibland seriekopplar vi system, det är bland annat så att en uppdelning i delsystem gör systemen mindre känsliga för avrundningsfel och andra effekter av begränsad ordlängd. Här får vi då använda insignalen för att beräkna det första systemets utsignal för att sedan använda denna utsignal som insignal när vi beräknar utsignalen från det efterföljande delsystemet och så vidare

Parallellkoppling

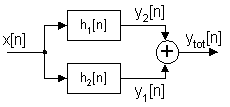
Även parallellkoppling av system förekommer och skälet är även här ofta att minska beräkningsfelen. Här har alla delsystem samma insignal och vi får enligt superpositionsprincipen den totala utsignalen genom att addera ihop de olika delsystemens utsignaler tidpunkt för tidpunkt

Korrelation

En användbar mätmetod i tidsplanet är korrelation där vi på olika sätt är ute efter att söka likheter mellan två signalers tidsföljder. I de flesta fall får vi tidsförskjuta den ena signalen i förhållande till den andra för att hitta likheterna.

Korskorrelation

Korskorrelatuion beskrivs av uttrycket

Här beräknar vi alltså produkten mellan de två signalerna tidpunkt för tidpunkt och summerar ihop produkterna. Vi gör beräkningen för olika tidsförskjutningar mellan de två signalerna. Vi letar då efter någon tidföskjutning där summan blir stor, vilket då visar att vi där har stor likhet mellan signalerna.

Metoden används till exempel i radarsammanhang där vi beräknar korskorrelationen mellan den utsända och den returnerade, reflekterade signalen. Den tidsförskjutning som ger maximal korskorrelation kan då översättas till avståndet till det föremål som reflekterade radarsignalen.

Korskorrelation används också i moderna mobiltelefonisammanhang där vi använder CDMA (Code Division Multiple Access). I CDMA överförs olika samtal på samma bärvåg men de är modulerade (blandade) med olika digitala kodmönster och vi använder då korskorrelation med de kända kodmönstren för att få fram de olikka signalerna.

Autokorrelation

Autokorrelation är en variant av korskorrelation där vi jämför en signal med sig själv

Detta kan synas konstigt då vi naturligtvis får bäst överensstämmelse då signalen ligger ovanpå sig själv, dvs då vi inte har något tidskift i ekvationen. Detta är sant men är signalen periodisk så kommer även andra tidsskift, som motsvarar ett helt antal perioder hos signalen, att ge ganska bra överensstämmelse och vi kan använda autokorrelation för att bestämma en signals period och därmed dess frekvensinnehåll.

Metoden används till exempel i bullerbekämpning av maskiner där signalens period ger oss möjlighet att koppla denna till rotationshastigheten hos olika komponenter i maskinen och därmed identifiera de delar som bullrar mest. Här kan vi naturligtvis även använda analysmetoder i frekvensplanet som vi strax återkommer till.

Frekvensplanet

Vi lämnar nu tidsplanet för att i stället se på signaler och systems egenskaper i frekvensplanet. Vi börjar med ett par grundläggande begrepp.

Periodisk signal

En signal är, som vi nämnt tidigare, periodisk om den har ett upprepande förlopp. Här kan vi skilja på två olika varianter. Alla periodiska signaler har en upprepande kurvform, det är dock inte säkert att vi har exakt samma samplingspunkter i varje period.

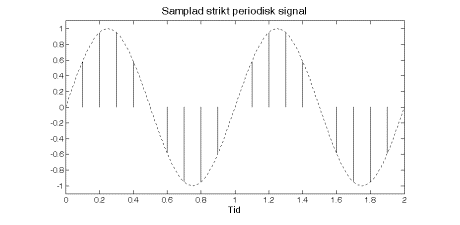
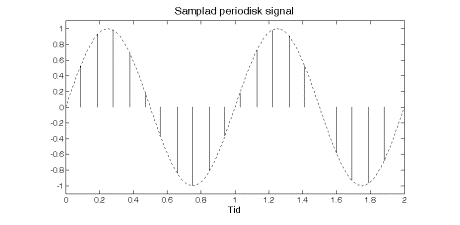
Skulle vi ha exakt samma samplingspunkter så kallas signalen för strikt periodisk. Resonemanget leder till att en signal kan ha en periodtid och en annan tid som är den strikta perioden. Den strikta perioden måste dock vara ett helt antal ’vanliga’ perioder.

Aperiodisk signal

En signal är aperiodisk om dess tidsförlopp inte upprepar sig. Detta är naturligtvis det vanligaste även om en sådan signal kan innehålla periodiska element om vi betraktar den under en kortare tid, till exempel tonerna i ett musikstycke.

Fourierserie

Fourierserien är ett sätt att beskriva en periodisk signal i tidsplanet och den byggs då upp med hjälp av fourierkoefficienter som kommer från frekvensplanet. Här måste vi hantera en strikt periodisk signal.

Som vi har sagt så har en periodisk signal en periodtid och går vi längre i tid så kommer det tidigare förloppet att upprepa sig. Detta betyder då att alla delar av signalen måste upprepa sig under denna periodtid och det får som följd att vår signal bara kan innehålla delsignaler som har samma periodtid som den totala signalens periodtid, dvs en grundton, och signaler som under denna grundperiodtid gör ett helt antal perioder, dvs signaler vars frekvenser är heltalsmultiplar av grundfrekvensen. Dessa senare signaler sägs då vara övertoner till grundtonen. Samtidigt vet vi att en tiddiskret signal bara kan innehålla frekvenser upp till halva samplingsfrekvensen och detta leder då till slutsatsen att en periodisk tidsdiskret signal kan bara innehålla ett begränsat antal frekvenskomponenter. Dessautom kan vår signal innehålla en likspänningskomponent. Samma grundresonemang gäller i det tidskontinuerliga fallet men där har vi ingen övre frekvensgräns varför antalet frekvenskomonenter, i alla fall teoretiskt, kan vara oändligt.

Vår fourierserie kan nu tecknas

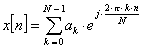
där är antalet sampel under en period av signalen. Det kan verka som om uttrycket ger frekvenskomponenter ända upp till frekvensen men detta är en skimär som beror av att vi använder exponentialfunktioner och inte trigonometriska funktioner.

På motsvarande sätt får vi fourierkoefficienterna ur ekvationen

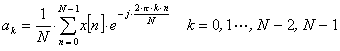
Även här får vi fourierkoefficienter för frekvenser över halva samplingsfrekvensen men dessa är spegelkoefficienter som kommer att ha samma storlek som den koefficient som ligger lika långt nedanför halva samplingsfrekvensen som den aktuella koefficienten ligger över halva samplingsfrekvensen. De två koefficienterna kommer dock att ha olika tecken på fasvinkeln, dvs

Fouriertransform

Vi sa att fourierserien används för periodiska signaler. För aperiodiska signaler så får vi i stället använda fouriertransformen. Denna ger inte ett diskret antal frekvenskomponenter utan ett kontinuerligt spektra , naturligtvis begränsat av halva samplingsfrekvensen. Vår frekvensvariabel (egentligen vinkelfrekvens) är normerad med avseende på samplingsfrekvensen, dvs . Vi har

där då fourierseriens summa övergår till en integral på grund av det kontinuerliga spektrat. Observera att integrationen sker över intervallet , dvs hela frekvensintervallet från noll till samplingsfrekvensen.

Vi får fourierspektrat som

Förutom att beskriva signaler så har fouriertransfomen sin stora användning för att bestämma frekvensegenskaperna hos ett tidsdiskret system.

Om vi till exampel tar den tidigare ekvationen

så kommer denna i frekvensplanet att ge

Vi ser att vi har en vanlig algebraisk ekvation där vi kan lösa ut och .

och vi kan via division få överföringsfunktionen i frekvensplanet

Vi kan nu sätta in olika värden på , dvs olika frekvenser, i uttrycket och beräkna överföringsfunktionens belopp och fasvinkel, dvs systemets egenskaper i frekvensplanet.

Jämförelse mellan fourierserie och fouriertransform

Vi såg ovan att fourierserien kräver en periodisk signal och verkliga signaler är sällan periodiska och även om de så skulle vara så är det väl inte säkert att vi lyckas sampla exakt en period av denna signal. Man kan säga att vet vi att vi har exakt en period av vår signal så vet vi redan signalens frekvensinnehåll och då blir bestämmandet av fourierseriens koefficienter lite meningslös. Fourierserien är alltså inte så användbar för att analysera verkliga signaler, den är dock klart användbar för att skapa, syntetisera signaler med önskat frekvens- och fasinnehåll.

Ser vi på fouriertransformen i stället så kräver beräkningen av spektrat att vi har samplandeinav oändligt många sampel, vilket naturligtvis inte är möjligt. Inte heller fouriertransformen är alltså användbar för att analysera verkiga signaler.

Trots detta kan vi inte förneka att det borde finnas idéer att ta till vara från både serie och transform och det gör vi i DFT (Discrete Fourier Transform).

Slutssats: DFT

Vi kan se DFT som framtagen antingen från fourierserien eller från fouriertransformen.

Om vi betraktar fourierserien så minns vi att den krävde en periodisk signal. Nu har vi inte det i det allmänna fallet, men vad händer om vi ändå antar att de sampel av signalen som vi har tagit är en period?

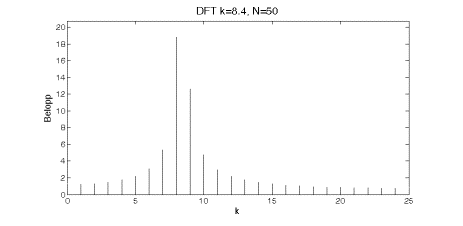
Vi kan räkna med att vi inte lyckas starta och sluta sampelserien på samma nivå så att vi får en mjuk övergång mellan ’perioderna’ utan vi kommer att få en abrupt övergång. Samtidigt har vi ju signalfrekvenser som inte ligger vid fourierseriens spektralkomponenter , vad händer med dessa? Det vore naturligt att anta att en signal med en frekvens som ligger mellan komponenterna och helt enkelt skulle ge bidrag i dessa två komponenter och det gör den också men det är tyvärr inte hela sanningen. Signalen kommer dessutom att ge bidrag i ett antal ytterligare foerierkoefficienter på båda sidor om den verkliga frekvensen. Vi får så kallat läckage.

Utgår vi i stället från fouriertransformen så har vi nu minskat antalet sampel från oändligt antal till stycken sampel. Fouriertransformens oändliga antal sampel gjorde att avståndet mellan varje frekvenskomponent blev oändligt litet och vi fick ett kontinuerligt spektra. Tar vi nu ett ändligt antal sampel så minskar vi upplösningen och får stycken diskreta frekvenskomponenter vid frekvenserna , . Vi kan säga att vi samplar fourierspektrat.

Uttrycket för DFT:n blir nu

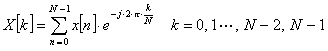
och vi får tidsserien via den inversa DFT:n, IDFT som

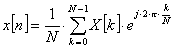
Vårt resonemang ger att en DFT-beräkning bara ger ett korrekt resultat om vi skulle råka sampla exakt en period av vår signal, men det är inte så sannolikt utan beräkningen blir en approximation. Ju fler sampel vi tar med i beräkningen ju bättre blir approximationen .

Fönster

Vi nämnde att vi i de flesta fall kommer att sampla ett intervall som ger abrupta övergångar mellan våra ’perioder’. Genom att dämpa de första och de sista samplen i vår följd så kommer vi att få en övergång som i stort sett ligger på nollnivå och övergången blir därmed mjukare. Vi säger att inför ett så kallat fönster.

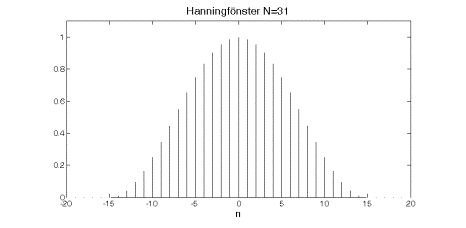
Det finns många olika varianter på denna dämpning i början och slutet av serien och det finns ett antal olika fönster som till exempel Hamming-, Hanning- och Blackmanfönster.

Rent allmänt kan man inte säga att något fönster är ’bäst’ utan de har lite olika egenskaper och det kan vara lämpligt att göra flera analyser av signalen med olika fönster för att få fram olika egenskaper hos signalen.

Effekten av denna signaldämpning är att läckaget inte når så många frekvenskomponenter på var sida om den verkliga frekvensen. Vi får dock inget gratis utan fönstren ger en mindre exakt analys i frekvensområdet runt signalfrekvensen.

Ibland använder man begreppet fönster även då vi gör den vanliga DFT-beräkningen och inte dämpar början och slutet av perioden. Vi har ju klippt ut stycken sampel ur den oändliga serien och detta kallas då för ett rektangulärt fönster.

FFT

Analys av DFT-beräkningen visar att en beräkning kräver ungefär multiplikationer och lika många additioner. Vill vi göra en noggrann beräkning, dvs beräkna över många sampel, så kommer beräkningen att ta lång tid.

Fast Fourier Transform (FFT) är ett genomtänkt sätt att genomföra DFT-beräkningen som gör att vi kan klara oss med färre antal beräkningar. Förutsättningen är att antalet sampel är en 2-potens, . Vi får ungefär multiplikationer och additioner vilket ger stora beräkningsvinster om antalet sampel är stort, 512 sampel ger till exempel 262.144 beräkningar i DFT-fallet och 4.608 beräkningar i FFT-fallet.

Det är värt att betona att FFT-beräkningen inte är en approximation av DFT-beräkningen utan vi får samma resultat i båda fallen. FFT-beräkningen är bara ett snabbarae sätt att genomföra beräkningen.

z-planet

z-plnaet är en generalisering av det tidsdiskrtea frekvensplanet på motsvarande sätt som s-planet (Laplaceplanet) är en generaliseringav det tidskontinuerliga frekvensplanet.

Definition av z-transform

Vi definierar z-transformen som

Tolkning

Hur tolkar vi nu z-transformen? Vi kan ur definitionen se att tidskift motsvarar multiplikation med , tidigareläggning ger plustecken på exponenten medan fördröjning ger minustecken. Det här betyder då att en signal har samma z-transform som den tidsskiftade signalen , med den skillnaden att den senare också får en exponent i z så att vi där har .

Har vi nu sammadifferensekvation som vi använde i frekvensplanet, dvs

så kommer denna i z-planet att ge

Där vi nu kan lösa ut och .och få överföringsfunktionen i z-planet

Frekvens i z-planet

Jämför vi ovanstående överföringsfunktion i z-planet med överföringsfunktionen i

frekvensplanet så ser vi att vi har samma uttryck förutom att är ersatt med . Eftersom så kan vi dra slutsatsen att frekvensplanets frekvenser ligger på en cirkel med radien ett runt origo i z-planet. z-planet är alltså en generalisering av frekvensplanet.

Poler och nollställen

Vi kan identifiera poler och nollställen i z-planet. Detta är punkter i z-planet där vårt uttryck blir oändligt stort respektive noll. Att utttycket blir oändligt stort innebär i praktiken att dess nämnare är noll medan det blir noll om täljaren är noll. Vi har till exempel för ovanstående uttryck nollställena och polerna

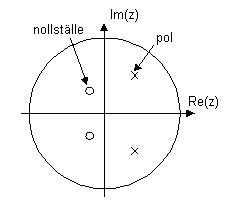
Komplexa poler och nollställen uppträder alltid i komplexkonjugata par.

Vi kan dra slutsatsen att vi inte får ha poler på enhetscirkeln eftersom detta skulle ge en oändlig överföringsfunktion och därmed bottning för någon frekvens.

Poler och nollställens inverkan

Då vi vill bestämma frekvensberoendet så rör vi oss alltså utefter enhetscirkeln i z-planet och vinkelområdet noll till pi, dvs övre halvplanet, vilket motsvararar våra tillåtna frekvenser, dvs noll till halva samplingsfrekvensen. Har vi nu ett nollställe nära enhetscirkeln så kommer täljaren i överföringsfunktionen att bli liten vid de frekvenser som ligger vid den vinkel där nollstället finns och därmed kommer överföringsfunktionen att bli liten för dessa frekvenser, dvs vi får en dal i beloppskurvan. Skulle nollstället ligga på enhetscirkeln så får vi total utsläckning vid denna frekvens.

Motsvarande resonemang ger att nämnaren blir liten då vi befinner oss nära en pol i z-planet och för dessa frekvenser kommer då överföringsfunktionen att bli stor och vi får en topp i överföringsfunktionens belopp. Ju närmare enhetscirkeln nollställe respektive pol ligger ju markantare blir dalen respektive toppen.

Vi kan också inse att den inverkan vi har i nämnaren ger kraftigare resultat än vad motsvarande inverkan i täljaren ger, detta betyder att poler har större inverkan på beloppskurvan än vad nollställen har. Går vi bakvägen till differensekvationen så ser vi att nollställen härstammar från transversella termer medan poler härstammar från rekursiva termer. Slutsatsen blir att rekursiva system kan ge kraftigare inverkan på våra signaler än vad transversella system kan.

Stabilitet

Våra system måste vara stabila och studium av poler och nollställens placering i z-planet ger att ett stabilt system måste ha alla poler innanför enhetscirkeln medan nollställenas placering i förhållande till enhetscirkeln inte spelar någon roll för stabiliteten.

Exempel

Låt oss ta ett par enkla exempel som visar hur vi kan använda pol/nollställesplacering för att få tidsdiskreta system med markant inverkan på våra signaler. Exemplen ger, trots sin enkelhet, kraftig inverkan på frekvensspektrat och skulle inte på något enkelt sätt kunna åstadkommas i ett analogt system.

Smalt bandpassfilter

Vi sa ovan att en pol nära enhetscirkeln gav en topp i vårt beloppsspektra. Vi kan skapa ett enkelt bandpassfilter som bara släpper igenom ett smalt frekvensområde genom att placera en pol nära enhetscirkeln vid den vinkel som motsvarar den frekvens vid vilken vi vill ha en toppen. Ju närmare enhetscirkeln vi placerar polen ju högre blir toppen och ju smalare blir filtrets bandbredd. Låt oss kallas polens radie . Vill vi ha toppen vid någon annan frekvens än noll och halva samplingsfrekvensen så måste polen vara komplex och då måste den kompletteras med sitt komplexkonjugat. Placerar vi våra nollställen i origo så kommer dessa inte att inverka på frekvensegenskaperna. Vi inför en förstärkningsfaktor för att kunna korrigera passbandsförstärkningen. Utan denna faktor blir passbandsförstärkningen för detta system alltid större än ett.

Vi får

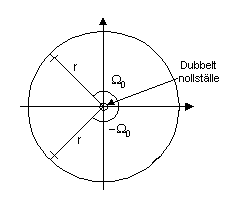
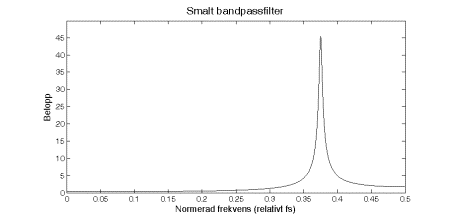
som ger differensekvationen

Notchfilter

Ändrar vi ovanstående system genom att flytta ut nollställena från origo och i stället placera dem på enhetscirkeln vid samma vinklar som polerna befinner sig så kommer systemets frekvensegenskaper att drastiskt förändras och vi får i stället ett smalt bandspärrfilter, ett så kallat notchfilter.

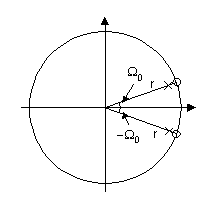
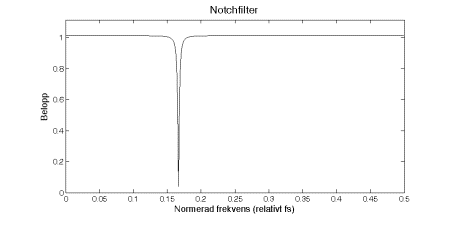
Vi får överföringsfunktionen

Systemstrukturer

Då vi vill realisera ett lite mer komplext system, till exempel ett system som har en överföringsfunktion av högre gradtal (många fördröjningssteg) så kan vi göra detta på lite olika sätt. Det rättframma sättet är naturligtvis att realisera systemets differensekvation som den är men det höga gradtalet gör att systemet lätt drabbas av avrundningsfel på grund av den begränsade ordlängden och vi får bättre resultat om vi delar upp systemet i serie- eller parallellkopplade sektioner.

Direktform och kanonisk form

Även då vi realiserar systemet som det är så kan vi välja att ordna de olika elementen lite olika och vi brukar tala om direkt form och kanonisk form. Den senare formen ger minst antal minneselement i realiseringen.

Tar vi ett andragradssystem som exempel så har vi differensekvationen

som kan illustreras med blockschemat

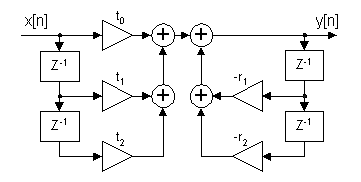
Om vi omformar blockschemat till kanonisk form så får vi

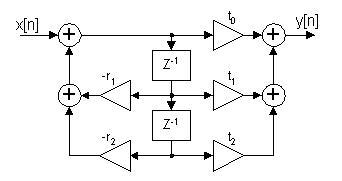
Detta system kan inte realiseras som en enda differensekvation utan vi får realisera ett system av differensekvationer enligt

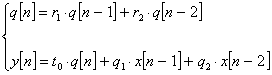
Biquad

Ovanstående andragradslänk brukar kallas för en biquadlänk och denna används som byggblock för att realisera mer komplicerade system.

Seriekoppling

Vid seriekoppling av system så seriekopplar vi biquadlänkar och utsignalen från en länk blir då insignal till nästa länk. Skulle vårt system ha udda gradtal (udda potens av z) så får en länk vara en förstagradslänk.

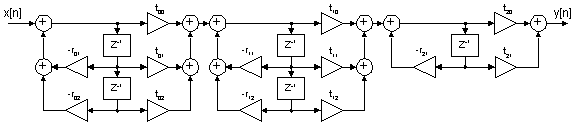
Parallellkoppling

Även här använder vi biquadlänkar som dock får lite anorlunda utseende jämfört med seriekopplingsfallet, täljaren får bara gradtal ett. Här har alla länkar samma insignal och den totala utsignalen skapas som summan av delsystemens utsignaler.

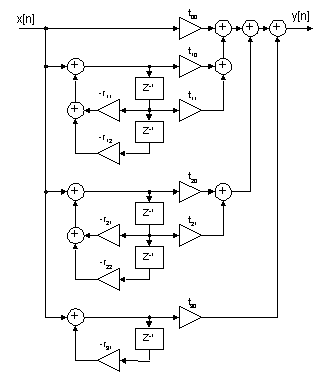
Filterbegrepp

Vi har i den tidigara texten snuddat vid en del filterbegrepp som gränsfrekvens, passbandsförstärkning och lågpassfilter. Låt oss sammanställa ett antalav dessa begrepp.

Filtertyper

Vi brukar skilja på fyra olika filtertyper vars egenskaper kan uttydas ur deras namn. Vi tar dessa grundtypers ideala egenskaper först, dessa ideala egenskaper går dock inte att realisera i verkligheten utan vi får göra approximationer.

Ett lågpassfilter låter signaler med frekvens upp till någon frekvens passera medan frekvenser över denna frekvens spärras.

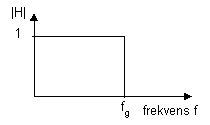
Ett högpassfilter låter i stället signaler med frekvens över någon frekvens passera medan signaler med frekvens under denna frekvens spärras.

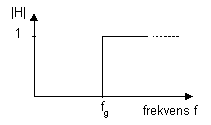
Ett bandpassfilter släpper igenom signaler med frekvenser mellan någon undre och någon övre frekvens medan övriga signaler spärras.

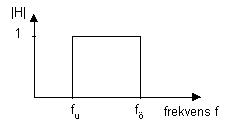
Ett bandspärrfilter släpper igenom signaler med frekvens under någon undre frekvens eller med frekvenser över någon övre frekvens. Signaler med frekvenser i intervallet däremellan spärras.

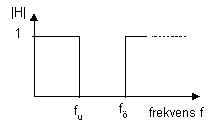
Det som är idealt i detta resonemang är att vi kan inte förvänta oss att övergången mellan det band där signalerna slipper igenom (passbandet) och bandet där de spärras (spärrbandet) är oändligt brant utan vi får ett övergångsband.

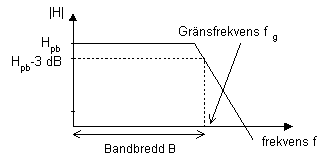
Samtidigt kan vi inte förvänta oss att signalera i spärrbandet dämpas ut fullständigt elöler att vi får en rät, horisontell linje i passbandet.

Grundbegrepp

Den frekvens som skiljer passband från spärrband kallas gränsfrekvens, har vi bandpass- eller spärrbandsfilter så har vi två gränsfrekvenser, en undre gränsfrekvens och en övre gränsfrekvens. I praktiken har vi en gradvis övergång mellan pass-och spärrband och vi måste definiera vilken punkt vi betraktar som systemets gränsfrekvens. Denna frekvens definieras som den punkt där förstärkningen har sjunkit till av nivån i passbandet, denna nivå motasvarar en sänkning med 3 dB om vi använder decibelskala.

I de flesta fall ökar brantheten hos övergången mellan pass-och spärrband med filtrets gradtal.

Rent idealt är grundfiltren sådana att signaler i passbandet passerar opåverkade, dvs de är varken förstärkta eller dämpade. I praktiken inför vi ofta en sådan faktor. Faktorn kallas passbandsförstärkning oberoende av om den är större än, lika med eller mindre än ett.

Linjär fas

Ett system som påverkar signalers frekvensegenskaper påverkar i de flesta fall inte bara signalernas storlek utan även deras fasvridning. Ett system där fasvridningen är linjärt beroende av frekvensen sägs ha linjär fasvridning. Sett på ett annat sätt betyder detta att alla signaler som passerar systemet kommer, oberoende av frekvens, att lika stor fördröjning och eventuella fasförskjutningar mellan komponenter i insignalen kvarstår i utsignalen. Detta är ofta en eftersträvansvärd egenskap och den kan inte uppnås med analoga system. Med tidsdiskreta system kan vi realisera detta men då måste vi hålla oss till transversella system men dessa har som vi nämnt en mindre inverkan på frekvenskurvan än vad rekursiva system har.

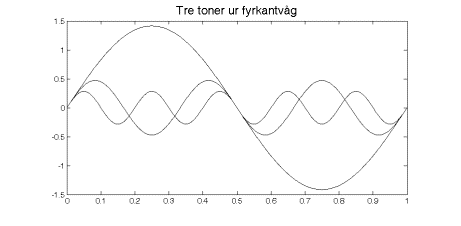
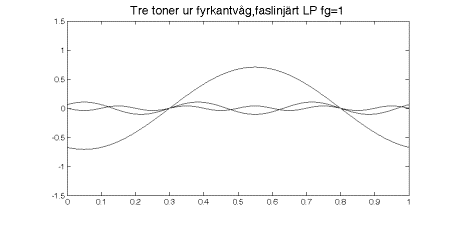
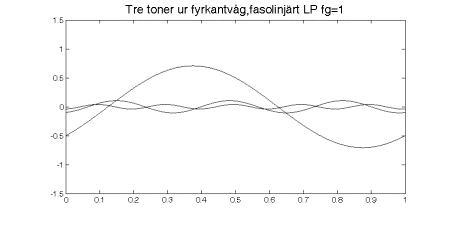
Det är inte alla som håller med om att olinjär fas är ett problem. I hifikretsar har detta ofta varit ett hett diskuterat ämne.

Transversella filter

Vi skall nu börja titta på metoder för att skapa filter, dvs system där vi önskar styra ett systems frekvensegenskaper på något sätt. Vi börjar med transversella filter, dvs system som bara innehåller tidsskiftade varianter av insignalen och ingen återkoppling. Vi skall nästan uteslutande se på kausala system.

Impulssvaret för ett transversellt system tar slut, dvs det är begränsat i tid och därför kallas dessa filter också FIR-filter (Finite Impulse Response).

Transversellt eko

Det enklaste transversella filtret är väl ett eko, dvs ett system där vi har en direkt signal medan vi fördröjer och eventuellt skalar en kopia av denna signal och sedan summerar ihop de två. Vi har

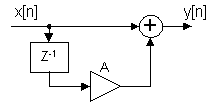
Betraktar vi systemet som ett eko så tänker vi kanske bara i tidsplanet och tänker inte på att vi också introducerar ett frekvensberoende. Vi såg redan tidigare på detta system då konstanten var ett och vi hade bara ett fördröjningssteg.

Vi kan genomföra samma resonemang i detta lite mer allmänna fall och får då till exempel om och

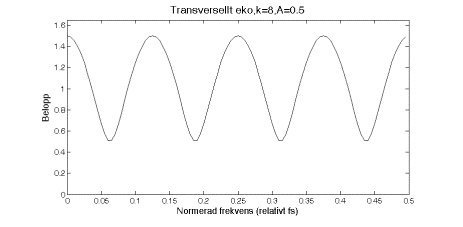
Transversellt kamfilter

I ovanstående system växer antalet toppar och dalar med fördröjningen och systemet brukar kallas för ett kamfilter.

Medelvärdesbildande filter

I ett medelvärdesbildande filter tar vi inte bara med den direkta signalen och en några steg fördröjd signal utan tar dessutom med alla mellanliggande fördröjningar och delar allt ihop med antalet termer, dvs

Ett medelvärde tar inte hänsyn till snabba förändringar hos en signal och det är väl inte direkt konstigt att vi här har en typ av lågpassfilter. Ju fler sampel vi tar med i medelvärdet ju lägre gränsfrekvens får filtret. Figuren visar som exempel ett medelvärdesbildande filter med 8 termer.

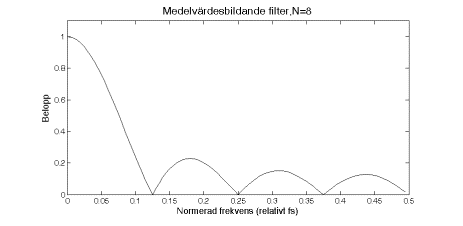
Invers fouriertransform

Vi har tidigare sett hur vi via invers fouriertransform kan få fram ett systems tidsfunktion, dvs dess impulsvar. Vi kan lätt inse att termerna i impulssvaret och konstanterna i motsvarande transversella filter är de samma och därför bör det gå att använda invers fouriertransform för att dimensionera filter. Vi hade

där vi kan sätta in den önskade filterkurvan i stället för . Rent allmänt är nu detta en komplex, frekvensberoende funktion som kan vara svår att integrera men håller vi oss till enkla grundfilter så går det bra. Har vi till exempel ett idealt lågpassfilter så skall ju alla signaler upp till någon frekvens slippa igenom, eventuellt skalade med någon passbandsförstärkning, för att för högre frekvenser ge total utdämpning. Vår funktion är alltså i detta fall bara en konstant som i två separata intervall har två värden och integralen blir enkel. Vi får om passbandsförstärkningen är och gränsfrekvensen är

Ett problem är att den inversa fouriertransformen bara ger korrekt resultat om vi ta med oändligt många termer i impulssvaret och vi kan naturligtvis inte ha ett filter med oändligt många termer. Vi väljer att ta med färre termer och får då ingen ideal kurva men vi kan i alla fall få något som liknar den önskade kurvan och ju fler termer vi tar med ju närmare idealet kommer vi så det är en avvägning mellan filterkurvans korrekthet och beräkningshastigheten.

Vi skall alltså ta med stycken termer. För att få korrekt filterform måste vårt ändliga koefficientantal bestå av symmetriska termer, dvs vi får beräkna termer för . Detta leder till att vi får ha udda antal termer. Det går även att ha jämnt antal termer men vi går inte in på detta här.

Ovanstående beräkningsuttryck fungerar inte för utan detta får vi beräkna för sig och får

Vi har nu alltså ett filter med symmetriska termer och ett sådant filter är inte kausalt utan hela uttrycket får fördröjas för att få kausalitet. Det icke-fördröjda filtret saknar fasvridning medan det fördröjda filtret kommer att få linjär fasvridning.

Vi kan diemnsionera de andra enkla filtertyperna som högpassfilter på motsvarande sätt.

Figuren visar som exempel beloppskurvan för ett lågpassfilter med gränsfrekvensen en fjärdedel av samplingsfrekvensen, passbandsförstärkningen 0,8 och med 35 termer.

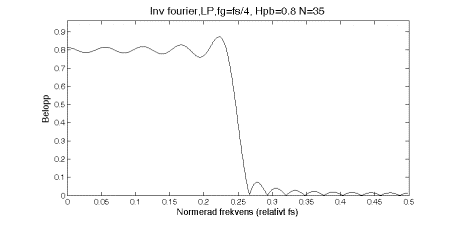
Fönster

Vi såg i exemplet ovan att det dimensionerade filtret har ganska kraftiga svängningar i beloppskurvan, både i pass- och spärrband. Svängningen kallas rippel. Vi kan dämpa svängningarna genom att behandla filtret med samma fönsterfunktioner som vi presenterade i samband med DFT-analys. Fönstren gör dock att övergången mellan pass- och spärrband blir mindre brant. Vi kan kompensera för detta genom att ta med fler termer i filtret men då blir ju beräkningen långsammare.

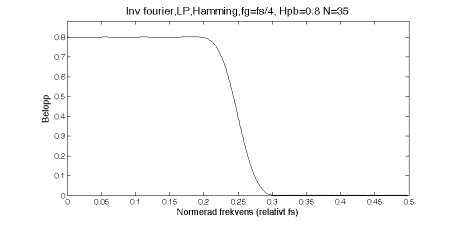
Frekvenssamplande filter

Vi såg nyss hur vi utgående från den inversa fouriertransformen kan dimensionera filter. Vi kan på motsvarande sätt utgå från ett samplat spektrum och används invers DFT för att få fram vårt filter. Antalet termer i filtret kommer då att bli lika många som det antal värden vi använder för att sampla vårt spektrum.

Väljer vi antalet sampel som en tvåpotens så kan vi även använda invers FFT för vår dimensionering.

Parks-McClellan

Resultatet av vår filterdimensionering via invers fouriertransform gav ett filter med ganska kraftigt rippel i pass- och spärrband. Vi kunde minska ripplet genom att använda fönster. Vi såg ur filterkurvan att ripplet är störst närmast övergången mellan pass- och spärrband.

Beräkningsalgoritmer har tagits fram för att fördela detta rippel jämnt över pass- och spärrband. Dessa filter kallas equirippelfilter och den mest kända beräkningsalgoritmen har tagits fram av Parks och McClellan och vi kallar filtren för Parks-McClellanfilter.

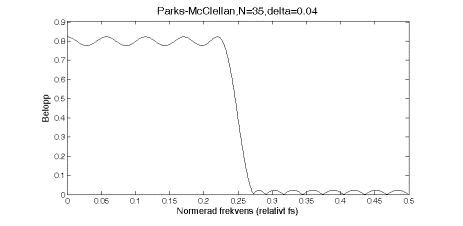
Rekursiva filter

Vi har nu sett på transversella filter. Vi kan generellt säga att dom kan inte användas för att ge snabba kraftiga variationer i frekvenskurvan. För att komma nära detta måste vi i alla fall ha högt gradtal på filtret, dvs vi får ha många termer i filtret och systemet blir långsamt. Ett positivt drag är dock att vi kan åstadkomma linjär fasgång i systemet.

Om vi övergår till rekursiva system där vi introducerar återkoppling, vilket innebär poler skilda från origo i z-planet, så kan vi få effektivare filter. Vi introducerar dock samtidigt olinjär fasgång i systemet och polerna gör att vi inför en risk för instabilitet.

Dessa system har ett impulssvar som i teorin aldrig tar slut även om det för stabilitet måste gå mot noll och då kommer att försvinna i systemets upplösning. Att impulssvaret inte tar slut gör att systemen också säges vara IIR-system (Infinite Impulöse Response).

Smalt bandpassfilter

Vi såg tidigare hur vi med enkla metoder kan skapa filter med smal bandbredd, dvs filter som filtrerar fram ett smalt frekvensområde med stor noggrannhet.

Notchfilter

Vi såg också hur vi på liknande sätt kan dimensionera filter som filtrerar bort ett smalt frekvensområde. Filtret kan till exempel användas för att filtrera bort en smalbandig störsignal. Det kan till exempel vara frågan om att filtrera bort nätbrum som härstammar från de 50 Hz som är frekvens i vårt vanliga elnät.

Rekursivt eko

Vi såg också hus vi kunde skapa ett enkelt eko med en direkt och en fördröjd signal. Vi kan göra en rekursiv variant av detta genom att i stället använda en direkt signal och en fördröjd och skalad utsignal, dvs

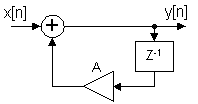
Detta system kommer då att fungera så att en signal som kommer in i systemet först kommer ut direkt och efter fördröjningen kommer signalen ut en gång till skalad med faktorn , varefter den efter en ny fördröjning kommer ut skalad med faktorn och så vidare. Det är lätt att inse att skalfaktorn måste ha ett belopp mindre än ett för att vi inte skall få en utsignal av konstant eller växande storlek som skulle bottna systemet. Detta är i samklang med vårt tidigare påstående att alla poler måste ligga innanför enhetscirkeln för att systemet skall vara stabilt.

Om vi använder samma konstanter som för det transversella ekot, dvs och , så får vi spektrat.

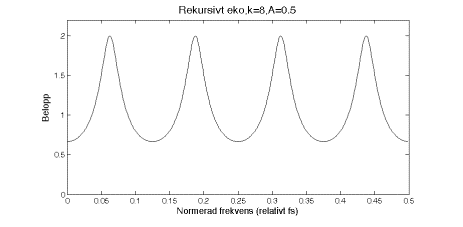
Rekursivt kamfilter

Vi ser att även det rekursiva ekot ger ett antal toppar i frekvensspektrat som den här gången är de smalare än vad de var i det transversella fallet. Systemet kallas också för ett rekursivt kamfilter.

Frekvenssamplande rekursiva filter

Genom att bygga upp ett system där vi använder ett transversellt kamfilter och ett antal rekursiva länkar så kan vi skapa så kallade rekursiva frekvenssamplande filter. Metoden går ut på att skapa en ny frekvenskurva genom att eliminera några av de nollställen som finns i kamfiltrets pol/nollställesdiagram genom att via de rekursiva länkarna, så kallade resonatorer, placera poler i samma punkter som dessa nollställen.

Metoden är ganska svår att få grepp om och dessutom rätt svår att implementera så vi går inte in på den här.

Tidskontinuerlig avbildning

Analog filterdimensionering är välkänd sedan länge och det har tagits fram en mängd olika filterkarakteristikor som vi gärna vill ta med oss till den tidsdiskreta världen. Välkända filterfamiljer är till exempel Butterworth-, Tjebytjev- och Besselfilter.

För att göra denna övergång så använder vi metoder för att transformera över systemet från den tidskontinuerliga till den tidsdiskreta världen.

Bilinjär transform

En sådan metod är bilinjär där vi transformerar över det analoga systemets poler och nollställen från det tidskontinuerliga s-planet till det tidsdiskreta z-planet.

Metoden kallas bilinjär transform och går ut på att den tidskontinuerliga frekvensvariabeln ersätts av den tidsdiskreta funktionen . Samtidigt måste tidskontinuerliga fasta vinkelfrekvenser som gränsvinkelfrekvensen ersättas av sin tidsdiskreta motsvarighet 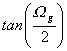där .

Avbildningen är inte helt linjär utan vi får avvikelser från motsvarande analoga filter då vi kommer nära halva samplingsfrekvensen.

Impulsinvariant avbildning

I den bilinjära transformen gjorde vi en transformering mellan de två generaliserade frekvensplanen (s- respektive z-plan). Vi kan också göra transformeringar mellan det tidskontinuerliga och det tidsdiskreta tidsplanet. Vi inför då en metod för att överföra det analoga systemets impulssvar till den tidsdiskreta motsvarigheten. Metoden kallas impulsinvariant avbildning. Metoden är inte lika vanlig som bilinjär transfom och vi går inte in på den här.

Adaptiva system

Vi nämnde tidigare att man i samband med mobiltelefoni måste använda signalbehandling som kan anpassa sig efter situationen eftersom signalförhållandena hela tiden ändrar sig beroende på att varje nytt samtal ger en ny uppkoppling som kanske sker via en ny basstation. Vi har också ändrade förhållanden beroende på att mobiltelefonen kan röra sig under samtalets gång.

System som på detta sätt kan ändra sina egenskaper dynamiskt kallas adaptiva system och används i första hand då vi vill minimera någon del av en signal då signalen och det vi vill ta bort är varierande. Det kan röra sig om att ta bort en smalbandig störning, en ton, vilket till exempel är fallet i system för att minska risken för rundgång i högtalarsystem. Omvänt kan det röra sig om att filtrera bort brus från en signal och filtreringen skall då bara ske i de frekvensområden som för tillfället saknar signal som vi vill behålla.

Adaptiva system används också vid talsyntes.

Algoritmerna är lite svåra att greppa men bygger på att via fördröjning och subtraktion identifiera periodiska element i signalen.

Wavelets

Wavelets är ett alternativ till DFT då det gäller frekvensanalys men wavelets kan också användas för datakomprimering i första hand i bilder.

Metoden bygger på att via ett hög- och ett lågpassfilter, båda med gränsfrekvensen en fjärdedel av sdamplingsfrekvensen dela in det totala frekvensområdet i två, frekvensmässigt, lika breda delar. Om vår signal från början består av stycken sampel så kommer vi nu att ha två serier med sampel i varje serie, dvs totalt sampel.

Eftersom det framfiltrerade lågpassbandet nu bara har hälften så stor bandbredd som från början så kan det klara sig med halva samplingsfrekvensen och vi halverar denna genom att utelämna varannat sampel, så kallad decimering, och har då kvar sampel. På liiknande sätt kan vi inse att även högpassbandet bara behöver halva samplingsfrekvensen och vi halverar även detta bands samplingsfrekvens. Vårt högpassband kommer då att ligga som spegelfrekvenser ovanför den nya halva samplingsfrekvensen (den ursprungliga fjärdedels samplingsfrekvensen) men detta är fullt möjligt att hantera då vi har filtrerat bort alla signaler med frekvenser under den nya halva samplingsfrekvensen. Även denna signal består nu av sampel och vi har totalt sampel som från början.

Vi kan nu stegvis gå vidare genom att dela in lågpassbandet i två nya lika stora delar och så vidare. Högpassbandet i varje steg lämnar vi dock som det är.

Vi har nu fått ett antal frekvensband där vi kan analysera frekvensinnehållet.

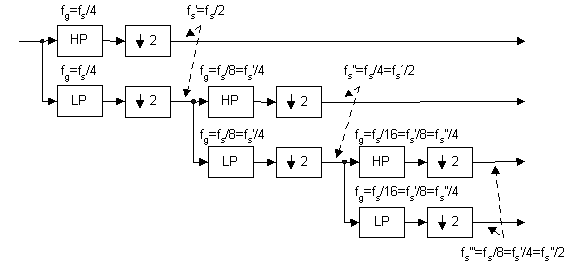
Vi kan också använda wavelets för datareduktion genom att helt enkelt ta bort svaga signaler i en del av frekvensbanden. Det visar sig att det ofta går att plocka bort svaga signaler som finns i enstaka frekvensband utan att det märks så mycket. Skulle vi göra samma sak på den ouppdelade signalen så skulle bortplockandet märkas tydligare.

Då vi nu har lagrat eller översänt den reducerade datamängden så skall totalsignalen återställas och då gör vi på omvänt sätt med nya filtreringar och höjningar av samplingsfrekvenserna via så kallad interpolering.

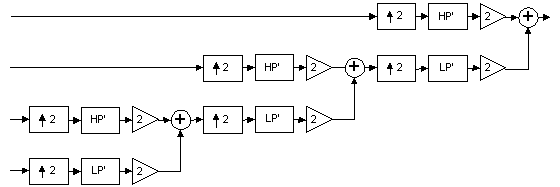
Det har visat sig att wavelets fungerar mycket bra för att reducera mängden information i pixeluppbyggda bilder (bitmap). I det sammanhanget är då höga frekvenser det samma som enstaka pixel medan låga frekvenser är block av pixlar med samma innehåll. Här har vi n tvådimensionell bild vilket gör att waveletsbehandlingen måste köras både horisontellt och vertikalt.

Ibland ser man på websidor bilder som sakta byggs upp genom att först visas en grovkorning bild varefter denna bild allt eftersom får allt mer detaljer. Detta är exempel på waveletsuppdelning av bilden.

Wavelets är grunden i standarden JPEG2000 för bildbehandling.