Book: Chapter 15. Lectures: Thursday, Friday, week 7.

Some answers are available.

The idea is that you should prepare these exercises at home, by yourself or with your group. If you have any questions, you can come to the exercise session and ask them to the assistants. (If you do not prepare in advance, there is little point in coming!)

Make sure you are comfortable with the following before you start the next exercises:

Chapter 15: Problems 15.1, 15.3, 15.4, 15.28.

Now please think about these.

1. You roll 2 dice. What is the probability that the two values that turn up are different?

You roll 3 dice. What is the probability that the three values that turn up are all different? What is the probability that there are at least two dice with the same value?

You roll n dice. What is the probability that there are at least two dice with the same value?

2. In Holland, license plates on cars have the following structure. They consist of a sequence of three groups of symbols. Each group is either a pair of two letters (from the alphabet A-Z, but not I, O, or Q) or of two digits (from 0-9). How many different license plates are there?

3. Given a prime number p. Show that

(	p	)
	k

Does this also hold when p is not prime?

4. How many triples (x,y,z) with x,y,z ∈ ℕ+ are there such that x+y+z = 10? How many are there such that x+y+z=N, for an arbitrary N?

Hint: imagine a chocolate bar with N pieces in a row. In how many ways can you chop it into three pieces of size x, y, and z?

5. Given the set A = {1,2,3,4,5}. How many strictly sorted lists are there of length 3 where all the elements come from the set A? A list is strictly sorted if the list is sorted, and no two elements are the same.

How many strictly sorted lists are there if A={1,2,3,...,n}, and the list length is k?

6. Prove Fermat's little theorem, namely that

a^p ≡ a (mod p)

for any prime number p, and any natural number a.

We have actually already proved this in the lecture. This time, do it by induction on a.

Let me help you: The base case (a=0) is easy: 0^p ≡ 0 (mod p) for any p > 0.

The step case assumes that k^p ≡ k (mod p) (this is the induction hypothesis), and has to show that

(k+1)^p ≡ (k+1) (mod p)

Hint: Make use of what you learned in exercise 3!

7. In the lecture, we used Pascal's triangle to prove that:

(	n	) + (	n	) = (	n+1	)
	k		k+1		k+1

8. You are taking a course with 54 students (including you). For the exercise sessions, you are randomly divided into 9 groups of size 6. You are secretly in love with one of your classmates (not yourself). What is the probability that the two of you end up in the same group?

9. (Inspired by Problem 15.38 in the book.) Use the Pidgeon Hole principle to show each of the following statements. Clearly indicate what the pidgeons are and what the holes are.

a. If everyone in this class sums up all 10 digits in their person number, there must be at least two students who end up with the same result. (Assume that we have 67 students and everyone's age is between 18 and 65.)

b. Given a set of 100 different integer numbers. There must be at least two numbers in the set whose difference is a multiple of 37.

c. Given 5 points within a unit square (not on the border). There must be at least two points that have a distance at most 1/√2 from each other.

10. Given n distinct nodes. How many different undirected graphs can we make from these?

11. Given a directed graph that is a bijection. This means that every node has exactly one outgoing arrow, and exactly one ingoing arrow. What is the probability that there is a cycle in the graph?

These exercises are for students who are looking for a challenge.

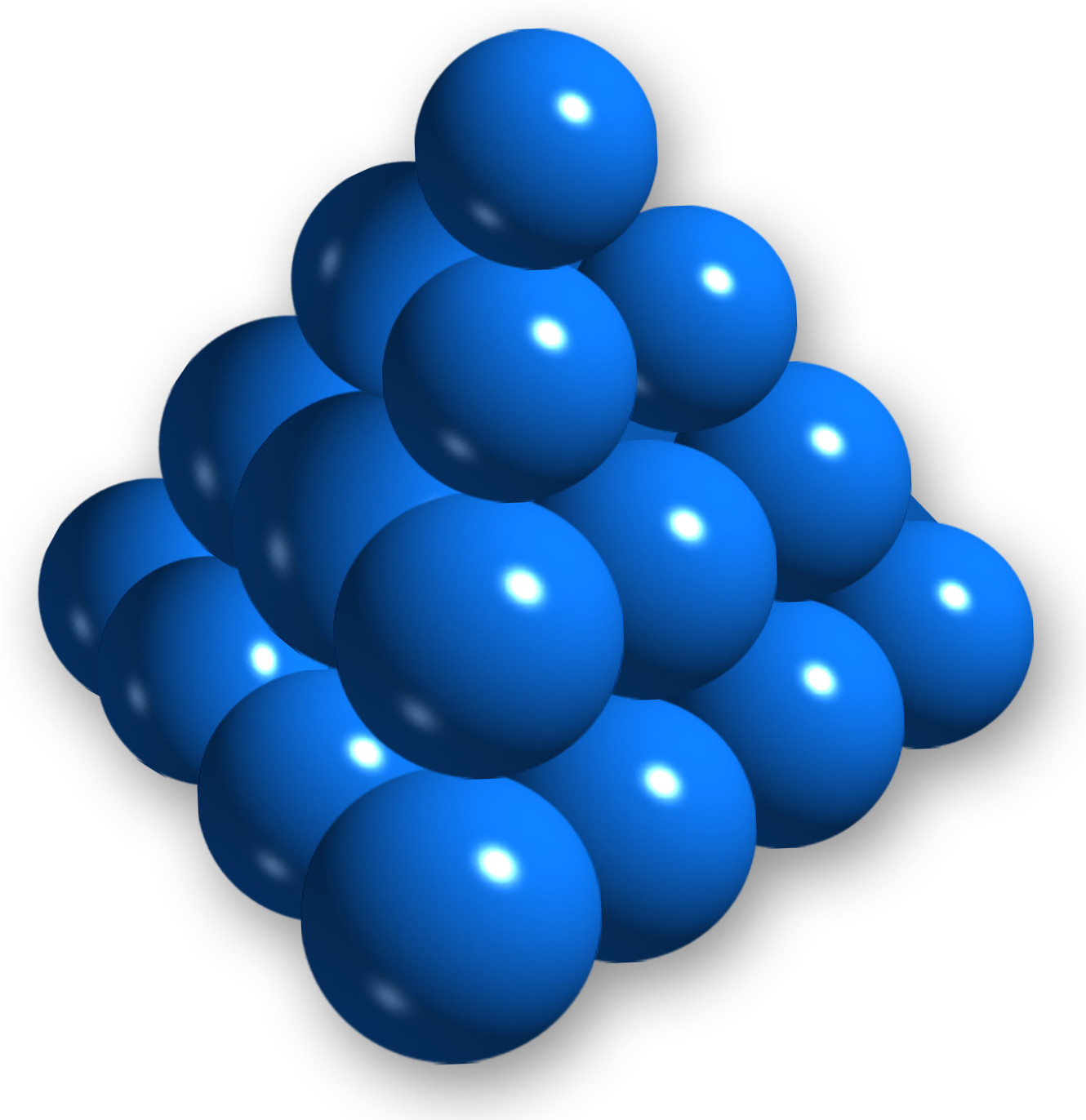1*. Take a look at the above picture of a triangular pyramid (or, actually, tetraeder) made out of blue marbles. If we express the number of needed marbles as a function of height, we get the following result: For a pyramid of height 1, we need 1 marble. For a pyramid of height 2, we need 1+3=4 marbles. For a pyramid of height 3, we need 1+3+6=10 marbles.

It turns out that the number of marbles for a pyramid of height n is:

(	n+2	)
	3

Hint: You can prove this by induction on n. But, you can also prove it directly by trying to associate each marble with a choice of 3 things out of n+2 things... Look at exercise 4 again and use what you learned there.

2*. Show that if the audience picks 8 cards from the deck of 52 cards, and the assistant reveals a sequence of 6 cards, the Magician can know the other 2 cards.