Here are some answers for the exercises.

1. The one on page 364 does not have a topological ordering, because there is a cycle: x1 <-> x3.

The one on page 399 has a topological ordering: A, B, C, D, E, F, G, H; every arrow in the graph only points from left to right in this sequence.

2. A cycle means that you can make a profit out of nothing, by buying one currency on the cycle, and then selling it for the next currency, until we get back to the beginning.

In reality, we have to be very quick, because market prices adapt to arbitrageurs from all over the world exploiting this very cycle!

3. There are 7 topological orderings: ABCGDEF, ABGCDEF, ABGDCEF, AGBCDEF, AGBDCEF, GABCDEF, GABDCEF.

We can get these by the following observation. First, we must choose between A or G as the first node. If we pick G, the next choice comes between C and D: 2 possibilities. If we pick A as the first node, we can either pick B or G as the first node. If we pick B, there are 3 possibilities. If we pick G, there are 2. 2+3+2=7.

4. R is reflexive: There is always a path from v to v for any node v (the empty path).

R is not symmetric. Consider the graph A->B, for which we have R(A,B) but not R(B,A).

R is transitive: If we have a path from u to v, and a path from v to w, we have a walk from u to w (glue the two paths together, with v in the middle). If we have a walk from u to v, we also have a path.

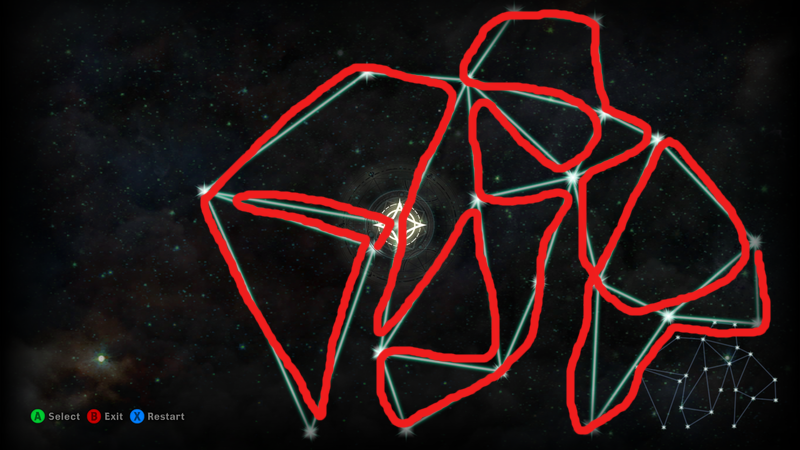
5. Fig. 12.3: Yes, there exists an Euler tour, because every node has degree 4, which is even. Start at any node. First, follow the inner edges that form a star, getting back to the same node. Now, follow the edges that take you around the graph.

Fig. 12.5: No, there are two nodes with degree 1, which is odd.

Page 488: No, all nodes except one have degree 3, which is odd.

6. There is no Euler tour because there are two nodes A, B, with degree 3. Since all other nodes have an even degree, adding one more edge between A and B must mean that there is an Euler tour. We get the Euler walk by finding the Euler tour with the extra edge, and then removing the edge. In other words, the Euler walk must start and finish with a node with an odd degree.

7. (a.) The number of components afterwards can either be 1 (the graph is still connected) or 2 (the graph was split into two components). Example for both: (1) G has three points with edges between each pair of points. (2) G has two points with one edge between.

(b.) The number of components afterwards can be anything: 0, 1, 2, 3, ... To see this, we will construct a graph G(k) that will fall apart into k components after removing one node v (you can choose k!). G(k) has one node v, plus k extra nodes. Each extra node has an edge to v. If we remove v, and all the edges connected to v, the number of components is exactly k.

(Note: technically, a graph with 0 nodes is not a graph, so you need to start with at least two nodes for this to work.)

8. R is reflexive: There is always a path from v to v for any node v (the empty path).

R is symmetric: If we have a path from u to v, then we also have a path from v to u (just take the reverse of the path).

R is transitive: If we have a path from u to v, and a path from v to w, we have a walk from u to w (glue the two paths together, with v in the middle). If we have a walk from u to v, we also have a path.

9. We do this by strong induction on n.

Base case: n=1. A tree with 1 node has no edges. OK.

Step case: n>=2.

The I.H. says that, for all 1 <= k < n, trees with k nodes have k-1 edges.

Now, we take a tree T with n nodes. There must be at least 2 nodes u and v (because n >= 2) and 1 edge e (because T is connected).

Now, remove the edge e.

The resulting graph consists of two separate components; one connected to u and one connected to v. (There cannot be more than two components, since every node is still either connected to u or to v. There cannot be one component, since that would mean there is still a path between u and v, which means that there was a cycle in T.)

Each component (by definition) is connected, and also has no cycle (because there are no cycles in T). So each component is a tree. Also, each component has less nodes than n, since each side has at least one node.

By the induction hypothesis, each component has 1 edge less than there are nodes. This means that the total number of edges for both components is n-2. This was after we removed one edge from T, so T has n-1 edges.

10. We do this by simple induction on n >= 1.

Base case: n=1. A graph with 1 node and no edges is a tree. OK.

Step case: Assume: Any connected graph with k nodes and k-1 edges is a tree. (I.H.)
Show: A connected graph with k+1 nodes and k edges is a tree.

Take a connected graph G with k+1 nodes and k edges. According to the lemma, it must have a leaf v. Consider the graph G' constructed by removing v and its one edge from G. G' is still connected (all other nodes still have paths to each other), has k nodes, and k-1 edges. So, G' is a tree. Specifically, G' has no cycles.

Now, we add back v and its edge, obtaining G again. There cannot be any cycles involving v (because it only has one edge), so G also has no cycles. Thus G is a tree.

11. We do this by strong induction on the length of the walk n.

Base case: n=0. The walk is already a path. OK.

Step case: n>=1.

The I.H. says that for all u, v, if there is a walk of length k < n between u and v, there also exists a path between u and v.

Suppose that we have u and v with a walk of length n. Either it is a path (in which case we are done), or it is not. If it is not, then there must be a node w that appears twice in the walk. The path thus looks something like: u--P--w--Q--w--R--v. Here, P, Q, R are walks going from u to w, w to w, and w to v, respectively. (Note that P and/or R may be empty, in which case u=w or v=w.)

Look at the walk: u--P--w--R--v, from u to v. It is certainly shorter than n, because we removed at least one step (the one involving w). So, by the I.H., there must be a path from u to v.

12. Proof by contradiction. Suppose we have a graph G with nodes u and v, two different paths from u to v, and no cycles.

Consider the subgraph G' that consists of exactly the two paths (the nodes and edges) between u and v. Clearly, G' is connected. Also, G' does not contain any cycles. So, G' is a tree. However, we know that in a tree, there exists only one unique path from u to v (which we showed in the lecture, and also in the book). This is a contradiction with our assumption.