You can find the questions here.

Question 1

Array C is a binary heap. (Array A has 17 as a child of 18, Array B has 9 as a child of 15.)

As a binary tree it looks like:

Root:                  3
2nd level:      5           18
3rd level:   7      15   22     35
4th level: 30 9   17

To remove the smallest element, 3, swap 3 and 17, and then sift 17 down. The result is, as a binary tree:

Root:                  5
2nd level:      7           18
3rd level:   9      15   22     35
4th level: 30 17

And as an array: 5 7 18 9 15 22 35 30 17.

Question 2

The sorted part of the array is in bold:

  1. 53 71 32 67 90 23 44 88 42 (insert 53)

  2. 53 71 32 67 90 23 44 88 42 (insert 71)

  3. 32 53 71 67 90 23 44 88 42 (insert 32)

  4. 32 53 67 71 90 23 44 88 42 (insert 67)

  5. 32 53 67 71 90 23 44 88 42 (insert 90)

  6. 23 32 53 67 71 90 44 88 42 (insert 23)

  7. 23 32 44 53 67 71 90 88 42 (insert 44)

  8. 23 32 44 53 67 71 88 90 42 (insert 88)

  9. 23 32 42 44 53 67 71 88 90 (insert 42)

Question 3

  1. The answers are B and D.

    The idea is: if node x is an ancestor of node y, then node x must have been added before y.

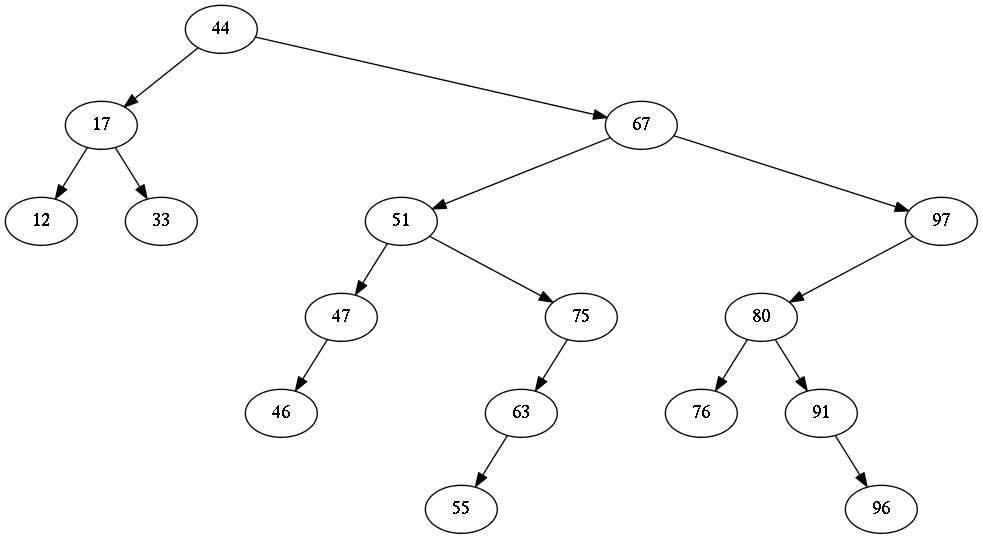
    In A, 67 is added before 76, but 76 is an ancestor of 67. In C and E, 67 is added before 63, but 63 is an ancestor of 67.

  2. Here is the resulting binary tree:

    reexam-tree.png

Question 4

The most important thing is that the pivot must end up after all the elements that are less than the pivot, but before all the elements that are greater than the pivot.

Here are my answers (the part of the array that still needs to be sorted is in bold):

  1. The pivot is 53.

    23 42 32 44 53 90 67 71 88

  2. The pivot is 23.

    23 88 32 44 53 90 67 71 42

  3. The pivot is 42.

    23 32 42 44 53 90 67 71 88

Question 5

data  = {f, g, c, d, e}
front = 4
rear  = 1

Question 6

  1. Here are two possible answers: 

    A B C D E F G H
A C D B G E F H

    Whatever order you choose, it must first visit all nodes that are neighbours of A, then all nodes that are 2 edges away from 3, then H (which is 3 edges away from A).

  2. See answer to question 6 here.

  3. See answer to question 6 here.

Question 7

You can use counting sort:

void sort(boolean[] array) {
    int count = 0;
    // Count how many elements in the array are false.
    for (int i = 0; i < array.length; i++)
        if (!array[i]) count++;
    // Write out the sorted array.
    for (int i = 0; i < count; i++) array[i] = false;
    for (int i = count; i < array.length; i++) array[i] = true;
}

Question 8

  1. The code does not work. If low == high then the function will return -1, even though array[low] might be the correct element.

  2. The code gives the correct answer still. However, in the worst case, it degenerates to linear search instead of binary search. This happens when the key is the last element of the array.

  3. The code goes into an infinite loop if mid == low.

Question 9

Following the hint, define perfect' :: Tree a → Maybe Int such that:

  • perfect' t = Nothing if t is not perfect

  • perfect' t = Just n if t is perfect and has height n. 

perfect' :: Tree a -> Maybe a
perfect' Nil = Just 0
perfect' (Node _ l r) = do
    hl <- perfect' l
    hr <- perfect' r
    guard (hl == hr)
    return hl
-- or without using do-notation:
-- perfect' (Node _ l r) =
--     case (perfect' l, perfect' r) of
--         (Just hl, Just hr) | hl == hr -> Just hl
--         _ -> Nothing

perfect :: Tree a -> Bool
perfect t =
    case perfect' t of
        Nothing -> False
        Just _ -> True