Warning! This is the 2012 course's website! You probably want the current course website.

Innehållförteckning veckovis:

vecka 11: introduktion, komplexitet, listor
vecka 12: stackar, köer, rekursion
vecka 13: binära sökträd, prioritetsköer, hashtabeller
vecka 16: självbalanserande sökträd
vecka 17: datastrukturer i Haskell
vecka 18: sortering
vecka 19: grafer

När du har gjort färdigt lösningarna, kan du tjuvkika på lösningsförslagen. (Men det tar en vecka eller mer innan jag lägger upp dem).

Vecka 11

Kapitel 1: Introduktion

Review questions: 8–10 på sid 55.
Programming projects: 1–2 på sid 55.
Skriv en metod som givet ett argument av typen int[], ett heltal samt ett index placerar in heltalet på den position som ges av indexet samt flyttar alla element i fältet med samma eller högre index ett steg "uppåt". Det sista elementet i fältet försvinner ur fältet om antalet tal i fältet skulle bli för stort. För att kunna testa metoden kan det vara bra att använda Arrays.toString(int[]a) i util-paketet. (Denna uppgifts idé används också i lab-uppgift 3 nedan).
Skriv en procedur/metod som givet två strängar flätar samman dem så att proceduren/metoden först tar en bokstav från den ena strängen sedan en från den andra ända tills någon sträng tar slut. Resten i den längre strängen läggs sist i resultatet. Att fläta samman strängen "anna" med "patrik" skall till exempel ge resultatet "apnantarik" (eller "paantnriak").
Gör en definition av en klass som är lämplig för att kunna representera ett datum på 2000-talet och en veckodag. Definiera också en metod i klassen som givet ett datum returnerar dess veckodag. Räkna med skottår vart 4:e år, men strunta i övriga småvariationer. Tips: Den 1 jan 2000 var en lördag.
I Java finns ju slumptalsgenertorn Math.random() som ger ett flyttal (double) i intervallet [0.0,1.0) med uniform distribution. Gör en egen variant av denna som istället ger heltal mellan MIN och MAX som resultat (MIN och MAX är parametrar). Prova sedan metoden genom att anropa den olika antal gånger samt skriv för varje gång ut en tabell som visar den relativa frekvensen för varje möjligt värde.

Avsnitt 2.4: Komplexitet

Self-check exercises: 1–4 på sid 87; 1–3 på sid 98.
Programming exercise: 1 på sid 87.
Review question: 5 på sid 144.
Ordna följande funktioner efter tillväxthastighet: n⁴, log n, n log n, 4n, 3n³, 5n² + n
Antag att du har en beräkning som kräver 2ⁿ steg och att varje steg tar en mikrosekund. Vilken är den största problemstorlek som kan lösas innan solen slocknar? Antag att solen slocknar efter 1,5768 · 10²³ mikrosekunder (5 miljarder år).
Nedan ges tillväxtstorleken för ett antal algoritmer. Vilka kan lösas inom rimlig tid om antal indata = 50?
1. 10 · 2ⁿ
2. 10000 · log₂ n
3. 100000 · n
4. 10 · n!
Skriv följande funktioner i Ordo-notation:
1. 34x + x²
2. 1x + 2x + 3x + 4x + 5x + 6x + 7x
3. 10⁴⁰⁰⁰x + 0,005 x² + 103/x³
4. 10 log₂ x + 2 log₁₀ x
5. 2^x + 10^x
6. (x–2) (x–1) x
Ange komplexiteten för följande KWArrayList-metoder, såsom de är definierade i avsnitt 2.3 i kursboken:
1. add(E)
2. add(int,E)
3. get(int)
4. set(int,E)
5. remove(int)

Kapitel 2: Listor

Self-check exercises: 1–2 på sid 77; 5 på sid 98; 2 på sid 103; 1 på sid 124.
Programming exercises: 1–2 på sid 69; 1–2 på sid 77; 2–3 på sid 98.
Quick-check exercises: 1–14 på sid 143–4.
Review questions: 1–3 på sid 144.
Programming projects: 1–3 på sid 145.
Vilken komplexitet har operationen att sätta in ett element sist i en enkellänkad lista som består av n element?
Vilken komplexitet har operationen att sätta in ett element först i en enkellänkad lista som består av n element?
Vilken konkret representation för listor skulle du välja om det inte får finnas någon begränsning av längden på dem och det måste gå snabbt att lägga till ett nytt element både i början och i slutet på listan. Dessutom ska operationerna att skapa en tom lista och ta bort första elementet finnas.
Vilken representation för listor skulle du välja om det inte får finnas någon begränsning av längden på dem och att det måste gå snabbt att ta bort både första och sista elementet. Dessutom ska operationerna att skapa en tom lista och att lägga till ett element först i listan finnas. Rita en tydlig bild och förklara varför det är en bra representation.
Antag att du vill ha en datastruktur med enbart operationerna insert, och findMin. Hur snabba kan du få operationerna? Ange representationen och beskriv kort hur operationerna går till.
Ge en algoritm som tar bort all kommentartext i ett program. Antag att kommentarerna skrivs (* ... *) och får förekomma nästade. Du behöver inte skriva någon kod utan det går bra att beskriva algoritmen i naturligt språk eller i en blandning av pseudokod och naturligt språk. Ange om du använder någon speciell datastruktur. Vilken komplexitet har din algoritm?

Vecka 12

Kapitel 3: Stackar

Self-check exercises: 1–3 på sid 152; 2 på sid 161; 1–3 på sid 169–70; 1–2 på sid 188.
Programming exercises: 1–3 på sid 152; 1 på sid 161; 1–2 på sid 170; 1 på sid 188.
Quick-check exercises: 1–9 på sid 189–90.
Review questions: 1–3, 5–7 på sid 190–1.
Programming projects: 2–4 på sid 191.
Ge en algoritm (och implementera den) som översätter infixuttryck till postfixuttryck. I uttrycken får förekomma tal, parenteserna (, ), och operatorerna +, *, med dess normala prioriteter. Exempelvis skall strängen "4+6*(2*6+10)" översättas till "4 6 2 6 * 10 + * +". Använd en Scanner för att läsa in strängen, och en stack för att lagra talen och operatorerna.
Ge en algoritm (och implementera den) som beräknar dessa postfixuttryck.

Kapitel 4: Köer

Self-check exercises: 1–3 på sid 152; 2 på sid 161; 1–3 på sid 169–70; 1–2 på sid 188.
Programming exercises: 1–3 på sid 152; 1 på sid 161; 1–2 på sid 170; 1 på sid 188.
Quick-check exercises: 1–8 på sid 238.
Review questions: 1–7 på sid 238–9.
Programming project: 9 på sid 241.
Ge en algoritm som ger en lista av elementen i ett binärt träd radvis (bredden-först). (Detta kräver att du tjuvkikar lite i kapitel 6).
Antag att du vill implementera en kö med hjälp av ett fält. Hur gör du för att operationerna skall bli så snabba som möjligt?

Kapitel 5: Rekursion

Self-check exercises: 1–2, 7 på sid 251; 1, 3 på sid 259; 1–2 på sid 267; 1–3 på sid 283; 1–2 på sid 288.
Programming exercises: 1, 3 på sid 252; 1, 4 på sid 259; 1 på sid 267; 2–3 på sid 289.
Quick-check exercises: 1–11 på sid 290.
Review questions: 2, 5, 7 på sid 290.
Programming projects: 2–3, 6–7, 9 på sid 291.
Gör stackuppgifterna 2 och 3 ovan (om att översätta/beräkna infixuttryck), fast använd rekursion så fort som du stöter på en parentes, istället för att använda en stack.

Vecka 13

Kapitel 6: Träd och sökträd

Self-check exercises: 3–5 på sid 303; 1–2 på sid 306; 1 på sid 314; 1–6 på sid 331–2.
Programming exercises: 1–3 på sid 314–5; 1–2 på sid 332.
Quick-check exercises: 1–5 på sid 355.
Review questions: 1–3 på sid 356.
Programming projects: 5–7, 11 på sid 356–8.
Ge elementen i följande binära träd i inorder, preorder respektive postorder:
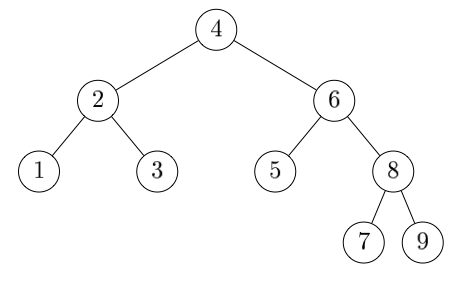
Bevisa eller motbevisa följande påstående:

Givet en bestämd mängd av objekt fås alltid samma binära sökträd oavsett i vilken ordning de sätts in i trädet.
Definiera en iterativ version av BST-metoden add(E item), vars rekursiva definition finns i listning 6.4 på sid 321–2 i kursboken.
(Svårt) Ange hur man kan modifiera ett binärt sökträd så att det går att hitta element nr k i sorteringsordningen, lika snabbt som ett enskilt element.
Exempel: Om trädet innehåller nycklarna 1,3,5,7,9,11,13,15,17 så är "5" element nr 3 i sorteringsordning och "15" är nr 8 i sorteringsordning. Hur går operationerna add(E) och findElement(int) till i ett sådant träd? Operationen find(E) ska fungera som för vanliga binära sökträd.
(Svårt) Skriv en linjär, O(n), funktion i Java som avgör om ett binärt träd är nivåbalanserat eller ej. Motivera varför funktionen är linjär, O(n). Ett nivåbalanserat träd får endast ha tomma platser längst till höger på understa nivån, enligt:

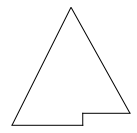
Avsnitt 6.5: Prioritetsköer

Self-check exercises: 1–4 på sid 344.
Programming exercise: 1 på sid 344.
Quick-check exercises: 6–8 på sid 355.
Review question: 4 på sid 356.
Bland följande animeringar finns även vanliga sökträd (BST) och heapar (Max Heap samt Min Heap):
- Olika sorters sökträd
- Många av de andra sökträden kommer vi att prata om i vecka 16
En prioritetskö är en kö där varje element i kön även har en prioritet. Varje gång ett element tas från kön skall det element med högst prioritet fås.
1. Antag att vi vill ha operationerna:
  - laggin: lägger in ett element i prioritetskön
  - tautmax: tar ut elementet med högst prioritet från kön
  - gemax: ger elementet med högst prioritet utan att avlägsna det från kön
  Föreslå några olika datastrukturer som kan användas för detta och ange hur operationerna kan utföras. Ange komplexiteten på operationerna och ev andra för/nackdelar.
2. Antag att vi även vill ha operationen
  - nyprioritet: ändrar ett elements prioritet i kön
  Hur kan den här operationen utföras för förslagen ovan? Komplexitet? Finns det någon bättre implementering?
3. Ange ytterligare operationer och hur de kan utföras.
Vad är skillnaden mellan en heap och en prioritetskö?

Hur kan man representera ett nivåbalanserat binärt träd i ett fält? Visa hur följande träd representeras.

                A
             __/ \__
            /       \
           B         C
          / \       / \
         /   \     /   \
        D     E   F     G
       / \   / 
      H   I J

Sätt in följande element i tur och ordning i en från början tom heap: 6 8 4 7 2 3 9 1 5

Kapitel 7: Hashtabeller

Self-check exercises: 1–3 på sid 371; 2, 4–5, 7–9 på sid 382–3; 1 på sid 395.
Programming exercises: 1–2 på sid 372; 1 på sid 383; 3–5 på sid 395.
Quick-check exercises: 3–7 på sid 415.
Review questions: 1–3 på sid 416.
Programming projects: 2–5 på sid 416.
Lek med följande animeringar:
- Hashtabeller, såväl öppen adressering som kedjning

Vecka 16

Kapitel 9: Självbalanserande sökträd

Self-check exercises: 1–2 på sid 476; 2–4 på sid 490; 2–3 på sid 502; (7 på sid 524).
Programming exercises: 1–3 på sid 490; 1 på sid 502.
Quick-check exercises: 1–2 på sid 532–3, (5–6 på sid 533).
Review questions: 1–3 på sid 534.
Programming projects: 1–2 på sid 534, (5–6 på sid 534–5).
Lek med följande animeringar:
- Olika binära sökträd
Bygg ett sökträd (BST, AVL, rödsvart, eller ett 2-3-träd, 2-3-4-träd, skiplista, eller varför inte ett B-träd?) med hjälp av animeringen i förra uppgiften, för meningen
"The quick brown fox jumps over the lazy dog"
Tyvärr går det inte bara att stoppa in heltal i animeringsträden, så vi måste översätta meningen till följande sekvens (kontrollera gärna att översättningen är korrekt):
1 8 2 4 5 7 9 6 3
Översätt slutresultatet till ett träd med de motsvarande orden istället för siffrorna (för varje trädtyp).
- För BST kan du jämföra med kursbokens figur 9.2 på sid 473.
- För AVL-träd kan du jämföra med kursbokens exempel 9.1 på sid 479-481.
- För rödsvarta träd kan du jämföra med kursbokens exempel 9.2 på sid 493-496.
- Kontrollera att animeringens AVL-/rödsvarta träd byggs på samma sätt som i boken.
- Tänk på att skiplistor är randomiserade, så resultatet blir olika varje gång.
För var och en av följande trädstrukturerer, avgör om den är nodbalanserad, höjdbalanserad eller nivåbalanserad:
1. Heap
2. Binärt sökträd
3. AVL-träd
4. Röd-svart träd
5. 2-3-träd, 2-3-4-träd, B-träd
6. Skiplista
Sätt in 2,1,4,5,9,3,6,7 i ett från början tomt:
1. Binärt sökträd
2. AVL-träd
3. Röd-svart träd
Bevisa eller motbevisa följande påstående, där X är BST, AVL, eller rödsvart:

Givet en bestämd mängd av objekt fås alltid samma X-träd oavsett i vilken ordning de sätts in i trädet.
Skriv Java-kod för dubbelrotation i ett AVL-träd (ej två enkelrotationer).
Bevisa eller motbevisa följande påstående, där X är BST, AVL, eller rödsvart:

I ett X-träd är skillnaden högst ett, mellan stigen till det bortersta lövet och stigen till den närmaste lövet.
(Svårt) Skriv Java-kod som givet en höjd returnerar ett AVL-träd med så få noder som möjligt, som har den höjden. Här är en Java-applet som gör just det:
http://people.cis.ksu.edu/~rhowell/viewer/minAVL.html
Försök att inte tjuvkika på källkoden :)

Vecka 17

Datastrukturer i Haskell

Obs! För att förenkla så finns all Haskell-kod från kompendiet som självständiga filer.

Implementera funktionen reverse :: [a] –> [a] genom att använda en Queue som hjälpstruktur. (Tips: du behöver två hjälpfunktioner: en som bygger kön och en som tar ut elementen för att skapa resultatlistan).
Ge en ordentlig komplexitetsanalys för funktionerna enqueue/dequeue i Queue-modulen. (Tips: antag att du först stoppar in n element och sedan tar ut dem, hur många operationer krävs då?)
Hur kan man implementera Queue med en enda lista? Ge en ordentlig komplexitetsanalys för enqueue/dequeue.
Definiera funktionerna preorder och postorder för binära sökträd. (Med samma typsignatur som funktionen inorder förstås).
Vad är problemet med att implementera en heap som i Java – som ett nivåbalanserat träd i ett fält / en lista?
Rita några heapträd som inte är nivåbalanserade.
Vilken är den stora nackdelen med heapträd, jämfört med en heap som ett kompakt fält?
Sätt in följande element i tur och ordning i ett från början tomt heapträd: 6 8 4 7 2 3 9 1 5
Implementera en sorteringsfunktion, binSort :: Ord a => [a] –> [a], som först bygger ett binärt sökträd och sedan returnerar elementen sorterade.
Implementera en annan sorteringsfunktion, avlSort, som gör samma sak fast med ett AVL-träd.
Implementera en tredje sorteringsfunktion, heapSort, som först bygger ett heapträd och sedan tar ut elementen ett efter ett.
Testa alla tre på några långa exempellistor, och se vilken som är snabbast. Jämför även med de givna implementationerna av insertionSort och mergeSort.
(Överkurs) Definiera en Haskell-klass för binära sökträd, och implementera om BinarySearchTree, AVLTree samt RedBlackTree som instanser av denna klass. (Med klasser menar jag dethär).
(Överkurs) Implementera en modul för 2-3-träd i Haskell.
(Överkurs, svårt) Läs på om andra heap-datastrukturer än nivåbalanserade träd, och försök implementera någon av dem: T.ex., leftist heap, skew heap, binomial heap, splay heap, pairing heap. De flesta finns beskrivna på Wikipedia, mer eller mindre begripliga. Om du är extra intresserad finns också artikeln "Playing with priority queues" i The Monad Reader nr 16. (Obs! Kursbokens nivåbalanserade heap kallas på många andra ställen "binary heap").
(Maxi-mega-jätte-överkurs) Läs boken Purely Functional Data Structures av Chris Okasaki. (Alternativt, om du inte vill köpa eller låna på bibblan, så kan du läsa hans doktorsavhandling helt gratis).

Vecka 18

Kapitel 8: Sortering

Self-check exercises: 1 på sid 424; 1 på sid 427; 1 på sid 435; 1 på sid 436; 1–2 på sid 446; 1–2 på sid 451; 1–2 på sid 460.
Programming exercises: 2 på sid 428; 2 på sid 435; 1 på sid 446; 1 på sid 460.
Quick-check exercises: 3 på sid 467.
Review questions: 1, 3, 6–8 på sid 467–8.
Programming projects: 5 på sid 468, (6 på sid 468).
Animationer att leka med:
- Flera olika sorteringsalgoritmer
- Ännu en bunt
Vilken komplexitet har operationen att leta upp ett element i ett osorterat fält bestående av n element?
Vilken komplexitet har operationen att leta upp ett element i ett sorterat fält bestående av n element?
Vilken komplexitet har operationen att sätta in ett nytt element i ett osorterat fält bestående av n element?
Vilken komplexitet har operationen att sätta in ett nytt element i ett sorterat fält bestående av n element (fältet skall vara sorterat efter insättningen)?
Sortera för hand sekvensen 4 6 8 2 9 5 1 7 3 med
1. insättningssortering (insertion sort)
2. urvalssortering (selection sort)
3. mergesort
4. heapsort
5. quicksort

Vilken komplexitet har följande sorteringsalgoritm?

     for ( i = 0; i < n-2; i++ ) 
        for ( j = i+1; j < n-1; j++ )
           if ( a[j] < a[i] ) {
               temp = a[i];
               a[i] = a[j];
               a[j] = temp;
           }

Har algoritmen några fördelar jämfört med övriga sorteringsalgoritmer?

En sorteringsalgoritm är stabil om lika element ligger i samma ordning efter som före sorteringen. Vilka av bokens sorteringsalgoritmer är stabila och vilka är inte det. Motivera!
Antag att du har ett fält av n element med enbart 2 olika värden, true och false. Ge en linjär algoritm som ordnar om fältet så att alla false element föregår alla true element. Använd endast konstant extra minne.
Implementera en sorteringsalgoritm baserad på binära sökträd. Dvs, bygg först ett binärt sökträd av den osorterade listan, och traversera sedan sökträdet in-order för att skapa den sorterade listan.

Vecka 19

Kapitel 10: Grafer

Self-check exercises: 1–3 på sid 547; 1 på sid 549; 1–3 på sid 559–60; 1–2 på sid 572; 1–4 på sid 588.
Programming exercises: 1 på sid 550; 1 på sid 560; 1–2 på sid 572.
Quick-check exercises: 1–10 på sid 590–1.
Review questions: 1–8 på sid 591.
Programming projects: 1 på sid 591, (6–7 på sid 592).
Animationer:
Implementera en grafmodul med följande operationer, och avgör vilken komplexitet de har:
1. skapa en tom graf utan vare sig noder eller bågar
2. lägga till en nod till en graf
3. lägga till en båge till en graf
4. ta bort en båge från en graf
5. ta bort en nod från en graf (och tillhörande bågar)
Utöka din grafmodul med följande operationer, och avgör vilken komplexitet de har:
1. antal bågar mot en nod i en graf
2. antal bågar från en nod i en graf
3. utskrift av noderna i en graf eller ge en lista av noderna
4. utskrift av bågarna i en graf eller ge en lista av bågarna
5. kontroll om en graf är sammanhängande
6. eget förslag
Skulle en annan representation av grafen medföra förändringar av operationernas (i föregående uppgifter) komplexitet? Vilka blir snabbare? Vilka blir långsammare?
En bipartit graf är en graf sådan att noderna kan delas i två mängder så att alla bågar går från en nod i den ena mängden till en i den andra mängden.
1. Ge exempel på en bipartit graf.
2. Ge en algoritm som avgör om en graf är bipartit. Ge algoritmen i pseudokod, inte programkod. Vilken komplexitet har din algoritm?

DIT960 | LP4 | VT2012 Datastrukturer DV[an error occurred while processing this directive]: Övningar