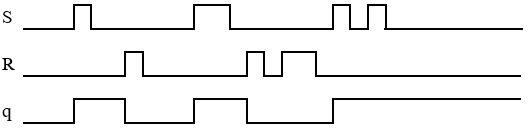
5.1 I figuren visas en SR-latch jämte tidsdiagram för S-, och R- signalerna. Komplettera tidsdiagrammet med q, då q =0 från början.

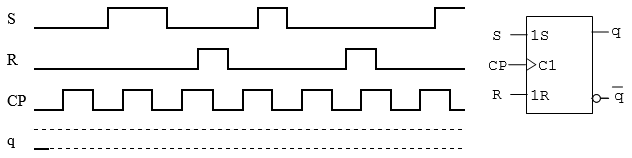
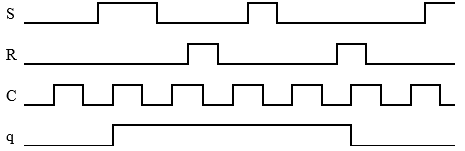
5.2 I figuren visas en SR-vippa jämte tidsdiagram för S-, R- och CP-signalerna. Komplettera tidsdiagrammet med q, då q =0 från början.

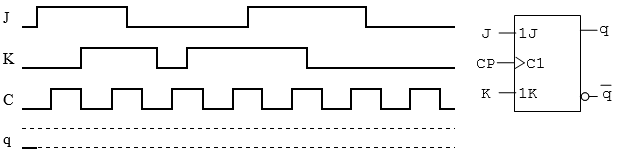
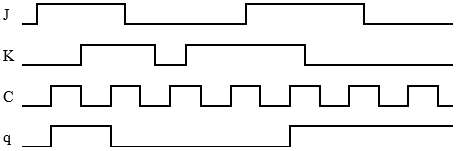
5.3 I figuren visas en flanktriggad JK-vippa jämte tidsdiagram för J-, K- och CP-signalerna. Komplettera tidsdiagrammet med q, då q =0 från början.

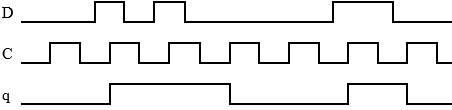
5.4 I figuren visas en D-vippa jämte tidsdiagram för D- och CP-signalerna. Komplettera tidsdiagrammet med q, då q =0 från början.

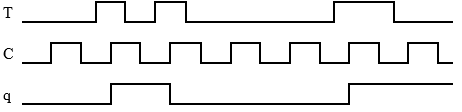
5.5 I figuren visas en T-vippa jämte tidsdiagram för T- och CP-signalerna. Komplettera tidsdiagrammet med q, då q =0 från början.

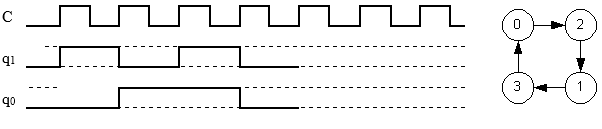
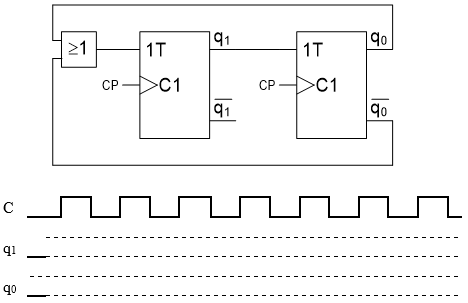
5.6 Rita tillståndsgraf och färdigställ tidsdiagrammet för den autonoma räknaren. Tidsdiagrammet skall utgå från tillståndet Q = (q₁q₀) = 0. (Börja med att ställa upp tillståndstabellen).

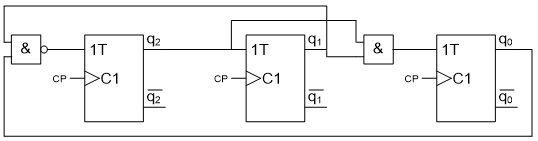
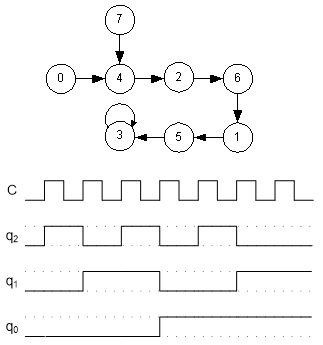
5.7 Rita tillståndsgraf och tidsdiagram för den autonoma räknaren. Tidsdiagrammet skall utgå från tillståndet Q = (q₂q₁q₀) = 0. (Börja med att ställa upp tillståndstabellen).

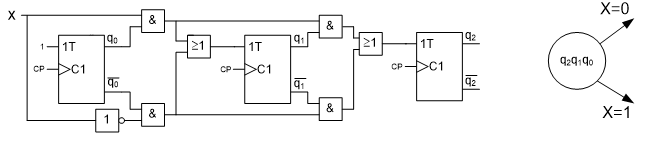
5.8 Ställ upp funktionstabell och rita tillståndsgrafen för följande räknare med räknevillkoret x.

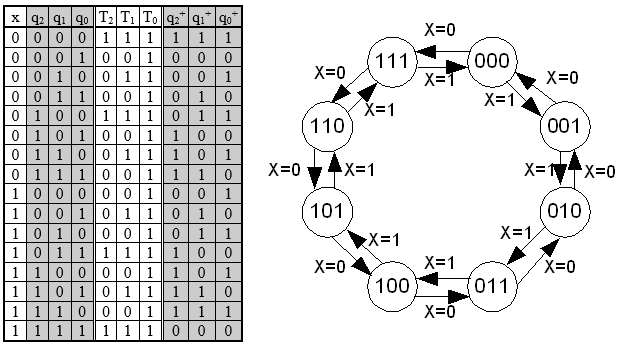
5.9 Ställ upp funktionstabell och rita tillståndsgrafen för följande räknare med räknevillkoret x.

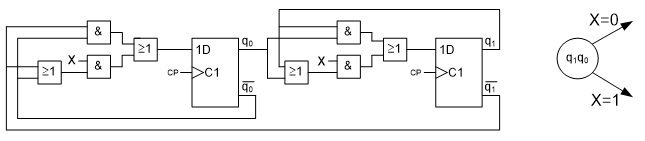
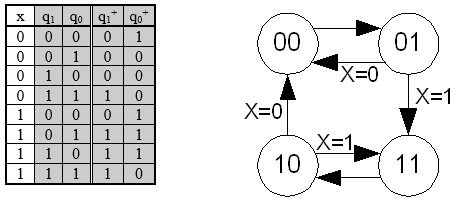
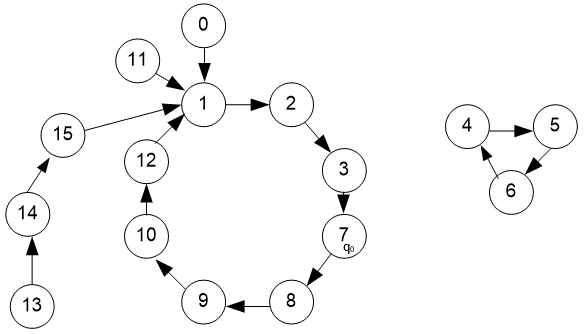
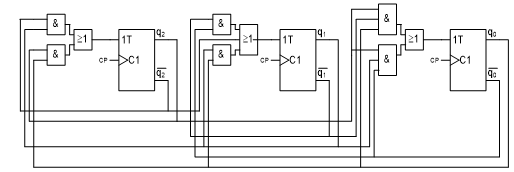
5.10 Analysera räknaren nedan. Utgå från initialtillståndet 0, vilken räknesekvens motsvarar räknarens tillståndsgraf? Tillstånden kodas som binärt tal: q₂ q₁ q₀. a) 0,1,2,3,4,5,6,7,0... b) 0,2,4,6,7,1,3,5,0... c) 0,2,4,7,6,1,3,5,0... alternativ b.

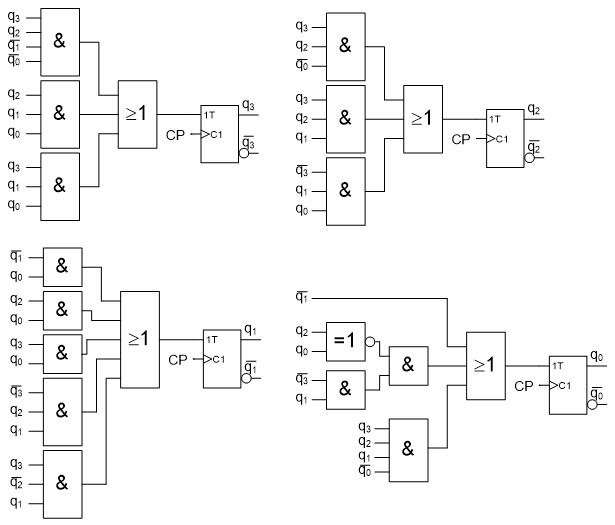
5.11 Analysera räknaren nedan. Visa dess fullständiga tillståndsgraf. Tillstånden kodas som binärt tal: q₂ q₁ q₀.

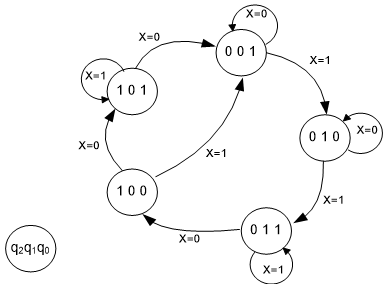
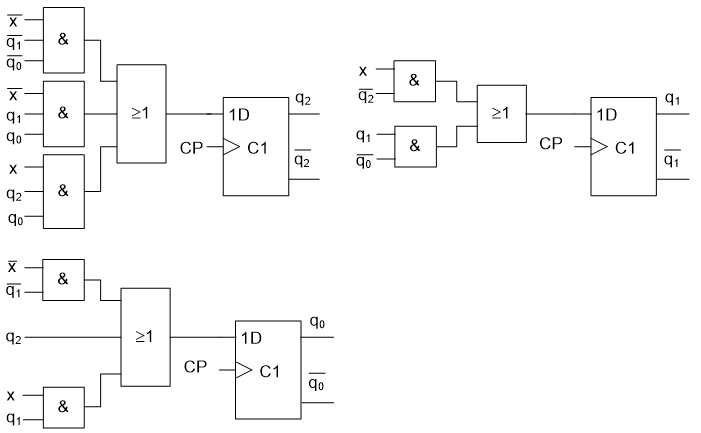
5.13 Konstruera en räknare med styrsignal x, som realiserar följande tillståndsgraf. Använd D-vippor, och grindarna AND, OR och INVERTERARE. Förutsätt att räknaren alltid startar i tillstånd 001.