Department of Computing Science
Chalmers University of Technology and Göteborg University
S-412 96 Göteborg, Sweden
oloft@cs.chalmers.se
Olof Torgersson
Department of Computing Science
Chalmers University of Technology and Göteborg University
S-412 96 Göteborg, Sweden
oloft@cs.chalmers.se
Even though declarative programming languages have been around for some thirty years by now they have still not gained any widespread use for real-world applications. At the same time object-oriented programming has conquered the world and is the methodology used for most programs developed today. This is a fact even though the used object-oriented languages like C++ lacks most features considered important in declarative programming like a clear and simple semantics, automatic memory management, and so on. It should be obvious that the object-oriented approach contains something that is intuitevely appealing to humans. Accordingly many attempts have been made to include object-oriented features into declarative programming and several languages like Prolog and Haskell have object-oriented extensions
In this note we discuss some existing declarative programming paradigms including definitional programming. In particular we will focus on control and also try to identify some characteristics that we feel it is necessary to incorporate in the next generation definitional programming language to gain success.
Most declarative programming languages stem from work in artificial intelligence and automated theorem proving, areas where the need for a higher level of abstraction and a clear semantic model of programs is obvious.
The basic property of a declarative programming language is that a program is a theory in some suitable logic. This property immediately gives a precise meaning to programs written in the language. From a programmers point of the the basic property is that programming is lifted to a higher level of abstraction. At this higher level of abstraction the programmer can concentrate on stating what is to be computed, not necessarily how it is to be computed. In Kowalski's terms where algorithm = logic + control, the programmer gives the logic but not necessarily the control.
According to [30] declarative programming can be understood in in a weak and a strong sense. Declarative programming in the strong sense then means that the programmer only has to supply the logic of an algorithm and that all control information is supplied automatically by the system. Declarative programming in the weak sense means that the programmer apart from the logic of a program also must give control information to yield an efficient program.
In functional programming languages programs are built from function definitions. To give meaning to programs they are typically mapped on some version of the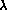 
-calculus which is then given a denotational semantics.
There are both impure (strict) functional languages like Standard ML [32] allowing things like assignment and pure (lazy) functional languages like Haskell [24].
Modern functional languages like Haskell come rather close to achieving declarative programming in the strong sense since programmers rarely need to be aware of control. On the other hand the execution order of lazy evaluation is not very easy to understand and the real computational content of a program is hidden under layers and layers of syntactic sugar and program transformations. As a consequence the programmer loses control of what is really going on and may need special tools like heap-profilers to find out why a program consumes memory in an unexpected way. To fix the behavior of programs the programmer may be forced to rewrite the declarative description of the problem in some way better suited to the particular underlying implementation. Thus, an important feature of declarative programming may be lost -- the programmer does not only have to be concerned with how a program is executed but has to understand a model that is difficult to understand and very different from the intuitive understanding of the program.
However, functional programming languages provide many elegant and powerful features like higher order functions, strong type systems, list comprehensions, and monads [43]. Several of these notions are being adopted in other declarative programming languages (see below).
Functional languages also support reusing code and come with a large number of predefined functions. While heavy use of such general functions give shorter programs it is not obvious that it makes programs easier to understand. An example of a general list reducing function is foldr which can be used to define almost any function taking a list and reducing it somehow:
fun foldr _ u nil = u | foldr f u (x::xs) = f x (foldr f u xs)Functional programming methodology makes heavy use of foldr and similar functions to define other functions recursing over lists. For instance the function len can be defined
val len = foldr (add o K 1) 0where add computes the sum of two integers and K is the K combinator. We leave up to the reader to understand how this definition works.
Heavy use of general higher-order functions, function composition, list comprehensions and so on, makes it possible to write very short programs but it also turns functional programming into an activity for experts only since it becomes impossible for non-experts to understand the resulting programs.
For practical applications there exists one logic programming in use: Prolog. Prolog is used for a wide variety of applications in artificial intelligence, knowledge based systems, and natural language processing. A (pure) Prolog program is understood as a set of horn clauses, a subset of first order predicate logic, which can be given a model-theoretic semantics, see [27]. Programs are evaluated by proving queries with respect to the given program.
From a programming point of view Prolog provides two features not present in functional languages, built-in search and the ability to compute with partial information. This is in contrast to functional languages where computations always are directed, require all arguments to be known and give exactly one answer. A simple example of how predicates can be used to compute in several modes and with partial information is the following appending two lists:
append([],Ys,Ys). append([X|Xs],Ys,[X|Zs]) :- append(Xs,Ys,Zs).Not only can append be used to put two lists together but also to take a list apart or to append some as yet unknown list to another one.
The built in search makes it easier to formulate many problems. For instance, if we define what we mean by a subset of a list:
subset([],[]). subset([X|Xs],[X|Ys]) :- subset(Xs,Ys). subset([_|Xs],Ys) :- subset(Xs,Ys).we can easily compute all subsets asking the system to find them for us:
| ?- findall(Xs,subset([1,2,3],Xs),Xss). Xss = [[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]
While the built-in search gives powerful problem solving capacities to the language it also makes the evaluation principle more complicated. Accordingly, Prolog and most other logic programming languages only provide declarative programming in the weak sense where the programmer also need to provide some control information to get an efficient program from the declarative problem description. The method used by many Prolog programmers is rather ad hoc: First the problem is expressed in a nice declarative fashion as a number of predicate definitions. Then the program is tested and found slow. To remedy the problem the original program is rewritten by adding control information (cuts) as annotations in the original code and doing some other changes like changing the order of arguments to predicates. The resulting program is likely to be quite different from the original one -- and less declarative. As an example, assume that we wish to define a predicate lookup that finds a certain element in a list of pairs of keys and values. If the element is missing the result should be the atom notfound. A first definition could be:
lookup(Key,[],notfound). lookup(Key,[(Key,Value)|_],Value). lookup(Key,[_|Xs],Value) :- lookup(Key,Xs,Value).However if we compute lookup(1,[(1,a),(1,a)],V) we will get the answer V = a twice and the answer V = notfound once. Of course in this case we have a logical error but the program can be rewritten using the same logic giving only one answer:
lookup(Key,[],notfound). lookup(Key,[(Key,Value)|_],Value) :- !. lookup(Key,[_|Xs],Value) :- lookup(Key,Xs,Value).The cut ( !) means that the third clause is never tried if the second can be applied. Note how this destroys the logic of the program (even if it gives the desired answers). A more efficient version can be defined if we swap the order of the two first arguments since it will allow the compiler to generate better code. Prolog also includes loads of impure features like arithmetic, meta predicates, operational I/O, and so on. All in all there exist few real Prolog programs which are truly declarative.
It is possible to incorporate notions like monads and list comprehensions into logic programming. For instance [8] shows how it can be done in the higher-order language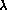 
-Prolog.
There are also languages trying to overcome the deficiencies of Prolog by providing cleaner mechanisms for control and meta-programming. An example is the language Gödel [23] which is a typed language based on a many-sorted logic.
A functional logic programming language tries to amalgate functional and logic programming into one (hopefully) more expressive language. In [30] it is argued that such a language should serve to bring together the researchers in the respective areas. This should speed up progress towards a truly declarative language. Unifying functional and logic programming should also make it easier for students to master declarative programming since they would only need to learn one language. The efforts to combine functional and logic programming mainly seem to come from the logic programming community trying to create more powerful and elegant languages by including functional evaluation and programming techniques into logic programming.
The two most commonly used methods for functional evaluation languages combining functional and logic programming is narrowing (see below) and residuation [1]. Languages using narrowing suspends evaluation of functional expressions until they are sufficiently instantiated to be reduced deterministically. Thus any mechanism for evaluating functions will do.
The theoretical foundation of languages using narrowing is Horn-clause logic with equality [35], where functions are defined by introducing new clauses for the equality predicate. Narrowing, a combination of unification and rewriting that originally arose in the context of automatic theorem proving [37], is used to solve equations, which in a functional language setting amounts to evaluate functions, possibly instantiating unknown functional arguments. Narrowing is a sound and complete operational semantics for functional logical languages. Unrestricted narrowing is very expensive however, so a lot of work has gone into finding efficient versions of narrowing for useful classes of functional logic programs. A survey is given in [21].
On an abstract level programs in all narrowing languages consists of a number of equational clauses defining functions:
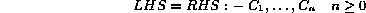
where a number of left-hand sides (LHS) with the same principal functor define a function. The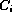 
's are
conditions that must be satisfied for the equality between the LHS and the right-hand side (RHS) to hold.
Narrowing can then be used to solve equations by repeatedly unifying some subterm in the equation to be
solved with a LHS in the program, and then replacing the subterm by the instantiated RHS of the rule.
Some examples of languages using narrowing is ALF [18,19], using a narrowing strategy correspnding to eager evaluation, and Babel [33] and K-LEAF [13] using lazy evaluation (narrowing).
As an example of a functional logic program and a narrowing derivation consider the definition
0 + N = N. s(M) + N = s(M+N).and the equation
X+s(0)=s(s(0)) to be solved. A solution is given by first doing a narrowing step
with the second rule replacing X+s(0) by s(Y+s(0)) binding X to s(Y). This gives the new equation
s(Y+s(0))=s(s(0)). A narrowing step with the first rule can then be used to replace the subterm
Y+s(0) by s(0), thus binding Y to 0 and therefore X to s(0). Since the equation to solve now is s(s(0))=s(s(0)) we have found the solution X=s(0).
An example of a language combining functional and logic programming taking a different approach is the language Escher [28,29]. Escher does not use narrowing as its operational semantics, nor does it build on first order predicate logic. Instead Escher programs are theories in an extension of Church's simple theory of types and programs are evaluated using a rewriting operational semantics, not a theorem proving one. Escher was designed with the specific goal of combining the best parts of the logic language Gödel, the higher order logic language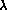 
-Prolog, and the functional language Haskell. Some features of Escher are ordinary logic programming capabilities, functional programming including higher order functions, list comprehensions and monadic I/0, built in set-processing, some higher order logic programming and so on.
The advantage of using a rewriting operational semantics is that no search is involved so each query has a unique answer and it should be possible to make the implementation more efficient. On the other hand Escher attempts to be so expressive that it may be hard to develop an efficient implementation anyway. The number of rewrite rules used in Escher is very large, well over one hundred. In [28] Lloyd writes
The rewrites were determined by experimentation -- when a term didn't reduce far enough, I simply added the appropriate rewrite to cope with this. In spite of this, the current collection (which I expect to be enlarged as the research progresses) does exhibit quite a lot structure and, roughly speaking, encompasses the capabilities of first-order unification, set unification and processing,In Escher the programmer provides control by giving mode declarations for each function (there are no predicates in Escher instead boolean functions are used). The following is an example of an Escher program (type definitions excluded) splitting a list into two sublists. Conceptually it defines a predicate Split even though it really defines a boolean function.-reduction, standard logical equivalences, and constructive negation. It's capabilities for higher order unification (...) are currently somewhat limited.
FUNCTION Split : List(a) * List(a) * List(a)
-> Boolean.
MODE Split : Split(NONVAR,_,_).
Split(Nil,x,y) =>
x=Nil & y = Nil.
Split(Cons(x,y),v,w) =>
(v=Nil & w=Cons(x,y)) \/
SOME [z] (v = Cons(x,z) & Split(y,z,w)).
The first line is a type declaration. The second provides control information. It means that a reduction of Split may only proceed if the first argument is not a variable. The underscores in the second and third arguments means that it does not matter what these are. Also note the explicit unification of x and y with Nil in the fourth line. Since Escher uses matching to find an appropriate clause only variables are allowed as patterns for arguments having an underscore in the mode declaration.
Escher always computes all solutions implied by the program so the
goal
Split([1,2],x,y)gives the answer
(x = [] & y = [1,2]) \/ (x = [1] & y = [2]) \/ (x = [1,2] & y = [])
The language Curry [22] is a recent proposal for a standardized language in the area of functional logic programming. The intention is to combine the research efforts of researchers in the area of functional logic programming and also, hopefully, researchers in the areas of functional and logic programming respectively. Thus boosting the development of declarative programming in general.
Curry is probably primarily an effort to design a language realizing research into efficient evaluation principles (narrowing strategies) for functional logic languages. However, in [22] it is stated that Curry should combine the best ideas of existing declarative languages including the functional languages Haskell [24] and SML [32], the logic languages Gödel [23] and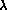 
-Prolog [34], and the functional logic languages ALF [18], Babel [33] and Escher [28].
The default evaluation principle in Curry is a sophisticated lazy narrowing strategy [5,20,31]
whose goal is to be as deterministic as possible and also to performs as few computations as possible. This strategy is complete in that it computes all solutions to a goal.
A simple example of a Curry program is the following:
function append: [A] -> [A] -> [A] append [] Ys = Ys append [X|Xs] Ys [X|append Xs Ys]This looks just like an ordinary definition in a functional language but can also be used to solve equations. For instance Curry computes the answer L = [1,2] to the equation
append L [3,4] == [1,2,3,4]Similarly, the ordinary map function can be defined:
function map: (A -> B) -> [A] -> [B] map F [] = [] map F [X|Xs] = [(F X)|map F Xs]Again, map can be used in the same way as in a functional programming language. However, if succ giving the next natural number is defined in the program, then the equation
map F [1,2] == [3,4]will give the solution F = succ. For details of how Curry handles higher order function variables see [4].
Predicates are represented as boolean functions using conditional equations. A simple example of this is following:
perm([],[]) = true.
perm([X|Xs],[Y|Ys]) = true <= select(Y,[X|Xs],Z),
perm(Z,Ys).
The second clause means that the result is true if the condition to the right of the arrow holds (evaluates to true). Some syntactical sugaring is also provided. An alternative definition for perm where select
is defined locally is:
perm([],[]).
perm([E|L],[F|M]) <= select(F,[E|L],N),perm(N,M)
where select(E,[E|L],L)
select(E,[F|L],[F|M]) <= select(E,L,M)
The where constructs is explained with an implications. An implication in turn is understood by adding clauses to the program in much the same way as in 
-Prolog.
The default evaluation principle in Curry is an attempt at declarative programming in the strong sense. However it is realized that it is not obvious that the lazy narrowing used as default is ideal for all applications. It is therefore possible to give control information in the form of evaluation restrictions. An evaluation restriction makes it possible to specify all sorts of evaluation strategies between lazy narrowing and residuation. If evaluation restrictions are used it is up to the user to ensure that the program computes all desired answers. To specify that the function append can only be reduced if its first argument is instantiated the restriction
eval append 1:rigidis added to the program. If append is called with a variable as first argument the call waits, residuates, until the variable is bound. As another example consider the function leg on natural numbers:
function leq: nat -> nat -> bool eval leq 1:(s => 2) leq 0 _ = true leq (s M) 0 = false leq (s M) (s N) = leq M NThe evaluation restriction means that the first argument should always be evaluated (to head-normal form), but that the second argument should only be evaluated if the first argument has the functor s at the top. Note that this might reduce an infinite computation to a finite one if the second argument can be reduced to infinitely many values. An alternative evaluation strategy, describing residuation, is
eval leq 1:rigid(s => 2:rigid)which corresponds to the mode declaration
MODE Leq : Leq(NONVAR,NONVAR).in Escher. Curry also allows the user to specify that a function should be strict by giving the evaluation restriction nf(normal form) for the arguments.
Curry also allows the user to give control information by use of encapsulated search. This means the search required due to logical variables and back-tracking,non-deterministic predicates or functions can be encapsulated into a certain part of the program. A library of typical search-operators including depth-first search, breadth-first search and so on is provided.
A constraint logic programming language performs deterministic computations over non-deterministic ones. We will not go into any details here but simply gives some examples of programs in the language Life [3]. A language using a concurrent constraint programming model related to constraint logic programming and aiming at several goals similar to those of Life (typically including object-orientation and functions evaluated using residuation) is Oz [38,39].
Life is formally a constraint programming language using a constraint system based on order-sorted feature structures [2]. Life aims at being a synthesis of three different programming paradigms: logic programming, functional programming and object-oriented programming. Life has many similarities with Prolog but adds functions, approximation structures and inheritance.
Pure logic programming in Life is very similar to programming in Prolog. Predicates are defined using Prolog-compatible syntax -- even the cut is included to prune the search space. Thus the same problems with control mixed with declarative statements as in Prolog is present. However, the presence of functions with deterministic evaluation makes it possible to write cleaner programs.
Life replaces the (first-order) terms of Prolog with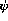 
-terms. The 
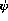terms are used to represent all data structures, including lists, clauses, functions and sorts. A 
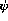term has a basic sort. The partially ordered set of all sorts may be viewed as a inheritance hierarchy. A sort may have subsorts and the subsorts of a sort inherit all properties of the parent sort. At the the top of the sort hierarchy we find 
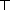written @ in Life. At the base of the hierarchy we fin 
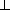written{}. There is no conceptual difference between values and sorts. For instance 1 is equal the set {1} which is a subsort of int. The sort int is a subsort of real, written int <| real.
The user is free to specify new sorts. The declaration truck <| vehicle means that all trucks are vehicles and also that trucks inherits all properties of vehicles. Now, if we define
mobile(vehicle) useful(truck)and ask the query
mobile(X),useful(X)?we will get the answer X = truck. A
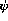term represent a set of objects. Each object can have attributes. Each attribute
consists of a label (feature name) and a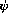 
-term:
car(nbr_of_wheels => 4,
manufacturer => string,
max_speed => real).
Note that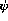 
-terms do not have fixed arities. It may even be possible to unify two 
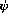-terms of the same
principal sort but with different arities.
Life also allows the use of functions. A function residuates until its arguments are sufficiently instantiated to match a clause. An example is:
fact(0) -> 1. fact(N:int) -> N*fact(N-1)Now if we ask the query
A = fact(B)?the system will respond with
A = @, B = @~. The tilde means that B is a residuation variable, that is, further instantiation of B might leader to further evaluation of some expression. If we state that B = 5 the call to fact can be computed and we get the answer A = 120. To use and define higher-order functions poses no problem since functions are evaluated using matching, that is, no higher order unification is needed.
In definitional programming a program is simply regarded as a definition. This is a more basic and low-level notion than the notion of a function or the notion of a predicate as can be seen from the fact that we talk of function and predicate definitions respectively.
So far there is one definitional programming language GCLA [6,7,25]. In GCLA programs are regarded as belonging to a special class of definitions, the partial inductive definitions (PID) [15,26]. Apart from being a definitional language there is one feature that set GCLA apart from the rest of the declarative languages discussed in this note, namely its approach to control. In GCLA the control (or procedural) part of a program is completely separated from the declarative description. A program consists of two definitions called the (object) definition and the rule (meta) definition, where the rule definition holds the control information. Both the definition and the object definition consists of a number of definitional clauses
where the atom a is defined in terms of the condition A. The most important operation on definitions is the definiens operation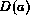 
giving all conditions defining a.
The separation of the declarative description and the control information means that there is no need to destroy the declarative part with control information. It also means that one definition can be used together with several rule definition giving different procedural behavior. Furthermore it means that typical control information can be reused together with many different definitions. It also means (unfortunately?) that for most programs the programmer has to be aware of control issues.
It is important to note that the rule definition giving the control information has a declarative reading as a definition giving a declarative approach to control. For more information on the control part see [6,11,26]
Assume we know that an object can fly if it is a bird and if it is not a penguin. We also know that Tweety and Polly are birds as well as all penguins, and that Pengo is a penguin. This knowledge is expressed in the following definition:
flies(X) <= bird(X),(penguin(X) ->false). bird(tweety). bird(polly). bird(X) <= penguin(X). penguin(pengo).To find out which objects cannot fly we can pose the query
(flies(X) \- false).and the system will respond with X = pengo. Note how this binds variables in a negated query.
As an alternative to the narrowing approach functional and logic programming can be combined in GCLA in a natural way. Since horn clause programs can be regarded as inductive definitions [17] (pure) Prolog is a subset of GCLA. How (first-order) functions can be defined and integrated with logic programs is described in [40,42,41]. It is also showed both how one library rule definition can be used for a large class of functional logic programs and how more sophisticated rule definitions can be generated automatically allowing more efficient definitions. We show an example that can be run using the library rule definition. Let the size of a list be the number of distinct elements in the list. We express this in the definition in the following way:
size([]) <= 0.
size([X|Xs]) <= (size(Xs) -> Y) -> if(mem(X,Xs),
Y,
s(Y)).
The second clause corresponds closely to a let expression in a functional langauge, that is, let y = size xs in ....
We also need to define the function if and the predicate mem:
if(Pred,Then,Else) <= (Pred -> Then),
(not(Pred) -> Else).
mem(X,[X|_]).
mem(X,[Y|Xs])#{X \= Y} <= mem(X,Xs).
Since GCLA uses logical variables and it is possible to bind variables in negation we can ask queries like
size([0,X,s(0)]) \- S.giving first the answer S = s(s(0)), X = 0, then S = s(s(0)), X = s(0), and finally S = s(s(s(0))),
0 \= X, X \= s(0). In particular note the third anwers telling us what X must not be bound to to make the sixe three.
Another programming technique is program separation. The principles of program separation using an idealized definitional language is thoroughly described in [9,10]. Here we simply give an example in GCLA. The idea of program separation is to separate an algorithm into its form and its content. The form implements the recursive form of the algorithm and the content fills the recursive form with the particular operations performed in the algorithm. It is natural to implement the form in a rule definition and use it together with different definitions to give different algorithms.
One form implementing several simple recursive algorithms can be described ``To compute F do the following: If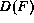 
is not a recursive call then the computation is finished, otherwise compute 
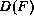to C and take as result of the computation 
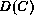.'' We can implement this as a rule definition in GCLA:
form <=
definiens(F,DF,_),
recursivecall(F,DF,B),
(formnext(B) -> ([DF] \- C))
-> ([F] \- C).
formnext(true) <=
(form -> ([F] \- C1)),
definiens(C1,SuccC1,_),
unify(SuccC1,C)
-> ([F] \- C).
formnext(false) <=
unify(F,C)
-> ([F] \- C).
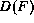is a recursive call if it has the same principal functor as F.
One example of an algorithm that has this form is addition. To compute m + n one has to be able to perform the following operations: move from 0 +n to n, move from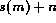 
to m + n, and take the successor of a natural number. These operations are defined as follows:
0 + N <= N. s(M) + N <= M + N. 0 <= s(0). s(N) <= s(s(N)).Now, combining form giving the recursive form, with the definition of the operations needed (the content), we get a program computing addition:
form \\ - s(s(0)) + s(0) \- C. C = s(s(s(0)))An example of an algorithm having the same form but different content is min computing the minimum of two natural numbers. To compute min we still need to get the successor of a natural number and also need operations to get from
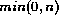to 0, from 
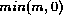to 0, and from 
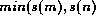to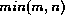 
:
min(0,_) <= 0. min(s(_),0) <= 0. min(s(M),s(N)) <= min(M,N).
While GCLA is an interesting first approximisation of definitional programming it is still to much of an extension to Prolog. Not only does it share first-order terms, logical variables, back-tracking and much of its syntax with Prolog, but it is also compiled into a Prolog program. The first GCLA programs were also clearly Prolog influenced. With new techniques being developed [41,42,9,10] it becomes clear that there is a need to refine the tools into a purely definitional language. Also in the Medview project [16] it has become clear that GCLA is not sufficient as modelling tool. Some problems (in no particular order) discovered are:
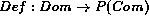and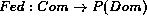 
. Def gives the definiens of a defined object while Fed gives the conditions in 
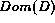that a given defining condition depends on.
Prolog.
In R. Kowalski and K. Bowen, editors, Proceedings of the Fifth
International Conference and Symposium on Logic Programming, pages 810--827.
MIT Press, 1988.
A Note on Declarative Programming Paradigms and the Future of Definitional Programming
This document was generated using the LaTeX2HTML translator Version 95 (Thu Jan 19 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 wm96.tex.
The translation was initiated by Olof Torgersson on Tue Mar 19 11:17:10 MET 1996