Denna övning handlar om att lära sig att programmera med rekursion.
Magnus Myreen, oktober 2016.
Övningen kräver endast en fil:
Main.java: programmet som ritar figurerKör programmet med att köra main i Main.java.
Main.java kommer med tre exempel: en spiral, ett rekursivt ritat träd och en triangel. Kör programmet så får du se dessa.
Main.java har också några extra metoder average, rotateX och rotateY som kan vara behändiga i övningens uppgifter.
Övningens alla figurer syns i följande video. OBS: programmet som du skriver behöver inte visa alla figurer i en körning. Videon visar i hörnet vilken uppgift som ritas. Det behöver inte din lösning göra.
https://www.youtube.com/watch?v=InVh7MnByZc
En funktion (eller metod) sägs vara rekursiv om den anropar sig själv. Klassiska exempel på rekursiva funktioner är fac som räknar fakulteten och fib som räknar Fibonacci nummer. Båda implementationerna nedan använder sig av anrop till sig själv, dvs de är rekursiva. Kör dessa i en debugger, t.ex. IntelliJs eller http://pythontutor.com/visualize.html#mode=edit för att se hur rekursionen fungerar.
int fac(int n) {
if (n == 0) { return 1; }
return fac(n-1) * n;
}
int fib(int n) {
if (n < 2) { return n; }
return fib(n-1) + fib(n-2);
}Både fac och fib kan skrivas som effektivare kod utan rekursion, men det finns flera algoritmer som är mycket svårare att skriva utan rekursion. Denna övning handlar om att prova på några exempel som är svåra att skriva utan rekursion. Använd rekursion i dina lösningar.
Se uppgift 1 i videon. Ditt program ska rita en stor låda. Inne i lådan ska programmet rita två lådor. Dessa två lådor ska var för sig följa samma mönster: de ska rita två lådor inuti sig och mönstret ska fortsätta.
Implementera detta genom att definiera en ny metod boxes med följande signatur. Anropa boxes från paintComponent metoden. Det är bra att använda double typen genomgående i dessa uppgifter.
void boxes(double x, double y, double width, double height, Graphics g) {
...
}Se till att rekursionen inte är oändlig. Om du glömmer att sluta rekursionen kommer programmet att köra fast i en java.lang.StackOverflowError. (Vad betyder detta? Använd Google så får du veta.)
Tips: Det lönar sig att testa halvfärdiga program. I detta fall kanske det lönar sig att börja med en implementation av boxes som endast ritar en låda utan rekursion alls. När det fungerar kan du sätta till rekursionen.
Se uppgift 2 i videon. Ditt program bör rita en trädliknande figur. Skriv en metod med följande signatur och använd den i paintComponent metoden.
void tree(double x, double y, double step, double angle, Graphics g) {
...
}Idén är att varje anrop ritar ett streck från punkten (x,y) till en punkt som ligger step pixlar ovanför punkten (x,y) men roterad enligt angle. Varje anrop ritar sedan två träd från slut punkter för strecket. Dessa nya träd bör ritas med olika värden för angle så att de utvecklar trädet i olika rikningar.
Se uppgift 3 i videon. Denna uppgift handlar om att rita en massa trianglar inuti en stor triangel. Det lönar sig att utgå från triangel exemplet som kom med orginal versionen av Main.java. Det lönar sig också att sätt till en extra parameter n som stoppar rekursionen på ett visst djup.
void recTriangle(double x1, double y1, double x2, double y2, double x3, double y3, int n, Graphics g) {
...
}För att animera ritningen så som i videon kan man använda klockans värde, dvs. s, som n i anropet till recTriangle i paintComponent . Obs: se till att du inte ber recTriangle gå för djupt med ett stort värde på n. Vad händer då?
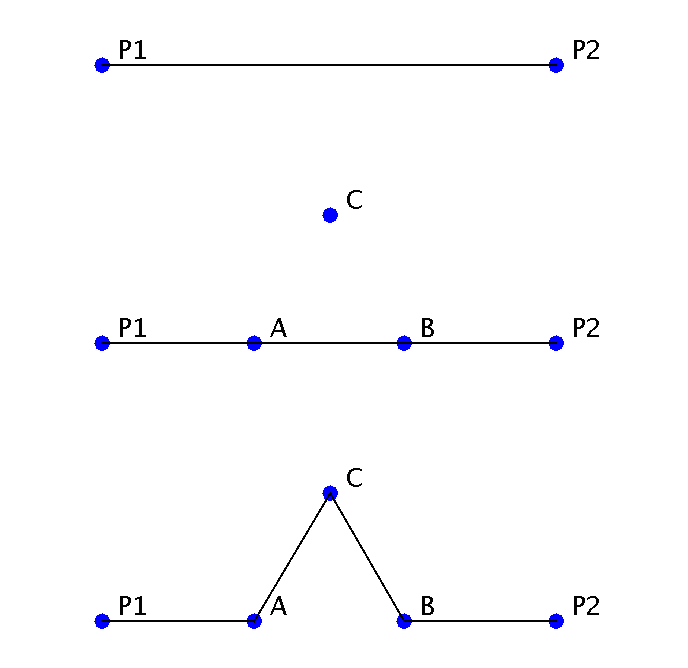
Se uppgift 4 i videon. Uppgift 4 ber dig rita en Koch snöflinga. En Koch snöflinga är en vanlig triangel som ritas med en rekursiv metod för strecken i triangeln. Varje streck i triangeln bryts upp med tre nya punkter som i följande bild. Sedan anropar man den rekursiva streck ritningensmetoden på de nya kortare strecken.

Det mest intressanta delen av uppgiften är beräkningen av punkterna som är markerade med A, B och C ovan. Punkterna A och C är lätta att hitta för att de ligger på linjen mellan ursprungs punkterna P1 och P2. Punkten C är aningen svårare att hitta. Observera att punkterna A, B och C är tillsammans en triangel vars sidor är lika långa, dvs varje varje vinkel i triangeln är 60 grader. Man kan alltså hitta C genom att rotera punkten B runt A med 60 grader.
Se uppgift 5 i videon. Denna figur ser kanske svår ut men är egentligen mycket enkel efter uppgift 4. I uppgift 4 pekar alla nya punkter utåt från mitten av triangeln. Din uppgift är att byta riktningen så att de nya punkterna alltid ritas inåt i triangeln.