Model Checking: A Complement to Test
and Simulation
Author: Gerardo Schneider
Model checking has been around for more than 20 years now, and has
migrated from the purely research to the industrial arena. Nowadays, it
is widely accepted that its application will enhance and complement
existing validation techniques as simulation and test. I try to explain
here in a non-technical manner what is "model checking".
* Notice that this is intended
to be "popular" account of what is model checking (always under
improvement) and thus the notions here are intensionally
informal, and maybe not completely precise. If you want a more formal
and precise account see for instance the wikipedia entry
and references therein.
INTRODUCTION
Our daily life dependency on computer-based applications (both hardware
and software) has motivated Computer Science researchers to develop new
techniques to increase our confidence on their correctness. Such
applications range from simple coffee machines to nuclear plants
passing by flight control towers. Many of those applications are
undoubtedly critical and a failure may cause high damages, both
economically and physically. Just to mention one of such big
catastrophes, the 4th of June 1996, the European rocket Ariadne
exploded just few seconds after launching, costing millions of dollars
and many years of lost work. An enquiry found that the error could have
been avoided with the use of formal methods techniques to detect the
software error which caused the disgrace. (For an account of this and
other "classic" software bugs, see for instance Garfinskel's
article.)
How can one be sure of the correctness of critical systems, with
thousands (and sometimes, millions) of components interacting in
complex manners? In some cases it is possible to build the system
under consideration, for instance the real chip, or coffee machine, and
then "feed" the system with sensitive data to check that it really
behaves as it is supposed to. This is the principle of "testing". Such
approach is widely used and extremely useful in practise, though it is
clearly not possible to use it in highly critical systems were the
testing data could cause damages in case of errors before real
deployment.
Another solution is to simulate the behaviour of the system on a
computer. Simulation does not work directly on the real system, but on
a model. A model is an abstract representation of the real system,
usually written using Mathematics or Logic. A model is to the real
system what an architect design is to the real house. One advantage of
simulation is that one does not need to build the real system in order
to be applied, and it is thus usually much cheaper than testing.
Both testing and simulation are widespread in industrial applications
and their used have been shown to be very useful. One drawback,
however, is that it is not possible, in general, to simulate or test
all the possible scenarios or behaviours of a given system. That is,
those techniques are in general not exhaustive due to the high number
of possible cases to be taken into account (sometimes infinite in
theory), and the failure cases may be among those not tested or
simulated.
Is there any other technique to complement testing and simulation? The
answer is yes: formal verification, a discipline lying on the border of
Mathematics, Logics and Computer Science.
FORMAL VERIFICATION
Formal verification comprises many different techniques, being the
common denominator their basis on solid mathematical and logical
foundations. In this sense, some researchers also include testing,
provided it is based on formal techniqques. We describe here one
technique called "temporal logic modal checking", which was introduced
in the beginning of the 80's, independently by Queille and Sifakis
(France) [5], and Clarke and Emerson (USA) [1].
In order to explain temporal logic model checking we need first to
understand what "temporal logic" and "automata" are.
Temporal Logic
In the same way as natural languages (e.g., Norwegian and English),
mathematical (classical) logic has syntax and semantics. Syntax
determines the rules to build well-formed words and sentences, whereas
semantics provides their interpretation or meaning.
There are sentences that are syntactically correct but not from the
semantic point of view. For instance "The big house is green" is both
syntactically and semantically correct (provided the house under
consideration is indeed green), while "The big house is small" is
contradictory as a sentence and thus semantically incorrect.
Logic takes into account syntactically well-formed sentences and
studies whether they are semantically correct. The interpretation in
usually given in a particular context, called "world". In normal
languages the context is given by dictionaries and the informal
real-life understanding of the words. In logic, a statement (syntax) is
commonly interpreted in a given semantic world. If the interpretation
is "true" in the given world (e.g., the big house is indeed green) then
one says that the statement is "satisfied" in the given world. A valid
and usual question in logic is: Is a given statement satisfied in a
given semantic world? In other words, is the statement true under the
interpretation?
One might be interested to know whether something will be true in the
future. For example, is it possible that "sometime in the future the
big house be green?". Such kind of statements can not be expressed in a
precise way in "classical logic", but in an extension of such logic.
In 1957 Arthur Prior [4] wrote an influential
article proclaiming the need
of a good symbolic formalism to analyse philosophical questions about
time. Time expressions such as "sometime in the future", "always in the
future" or "always in the past", can be expressed in the so-called
"temporal logic". Though the origins of such logic (first called "tense
logic") were in philosophy, its main application today is in Computer
Science, and in particular in the area of formal verification, thanks
to the seminal work of Amir Pnueli. Pnueli proposed in 1977 [3] to use
temporal logic as a framework to specify and reason about complex
programs.
Automata
An "automaton" may be defined to consist of a set of "states" and a set
of "relationships" between the states. States are usually depicted as
circles while relations are depicted as arrows between the states.
Arrows are often "decorated" with "labels" representing conditions or
actions. When the automaton is in a given state, it can change to
another state only if the given condition on an arrow connecting both
states is satisfied (or similarly, if the action takes place).
If there is an arrow from state A to state B, it means that A occurs
before B. Similarly, A must occur before C if there is an arrow from B
to C, and one says that B and C occur in the future of A.
As an example, let us consider an automaton modelling a simple coffee
machine (see Fig. 1).
Initially the machine is at state "Start" and it "waits" for a coin. If
a coin is provided then the machine change state to the "Button" state
where two options are possible: to press the "k" button and then go to
the "Coffee" state, or to press "t" and go to the "Tea" state. After
serving the corresponding drink, the machine goes to the "Glass" state
and it gives a glass with the chosen drink to then go back to the
"Start" state.
Temporal Logic Model Checking
When one builds a system to perform a given task it is common to define
a set of properties the system must satisfy. Model checking is a
technique used to answer to the following question: Does the system
satisfy the given properties?
Model checking does not work on the real system but on a model, and the
properties are usually not expressed in natural language but in a
formal language. Often, one represents the system as an automaton, and
the properties are written in temporal logic. We explain the method
with two examples.
Example 1.
The property "Always, after the machine gets a coin and the user press
a button, it gives coffee or tea", can be written in temporal logic as:
ALWAYS (IF Button THEN (SOMETIME-IN-THE-FUTURE (Coffee OR Tea)))
Words in uppercase are temporal logic "connectives" or "operators", and
the other words represent the interaction between the machine and the
user. The above expression is a "formula" of temporal logic.
How can one see that the given automaton satisfies a formula? We can
explain it by using the above formula and the automaton modelling the
coffee machine.
We need first to understand how the connectives ALWAYS, IF-THEN,
OR and SOMETIME-IN-THE-FUTURE are
interpreted in the automaton. Let us assume the current state of the
automaton is the initial "Start" state. Let A and B be statements, then
"ALWAYS A" means that A must be true in all the states of the
automaton. "IF A THEN B" means that whenever A is
true in a given state, so is B. "A OR
B" means that at least one of A and B must be true in the state.
Finally "SOMETIME-IN-THE-FUTURE
A" means that it must exist a state in the future of the current state
where A is true.
It is then possible to check that the above formula is satisfied by the
automaton, since from the state "Button" (after a coin is inserted) it
is possible to find a state in the future such that the actions
"coffee" or "tea" are possible.
Example 2.
Let us consider now the following property: "Always, after pressing a
button the machine will serve coffee and then tea immediately
afterwards". We can write this sentence as follows:
ALWAYS (IF Button THEN (Coffee AND NEXT Tea))
Here NEXT is a connective
formalising the "immediately after" English expression. As for the
previous example it is possible to check whether the automaton
satisfies the property. In this case we can see that it is not the
case, since from the state "Button" one can reach the state "Coffee"
and "Tea", but from the "Coffee" state it is not possible to go
immediately after to the "Tea" state. This property guarantees that the
machine will never allow (for the distress of the user and happiness of
the machine's owner) to get coffee and then tea by paying only once.
The above examples are rather simple and in both cases a simple
eye-inspection helps to give the correct answer. In general the
automaton corresponding to the system may be extremely big (of the
order of millions of states) and answering to such temporal questions
is far from obvious. Model checking tools can answer automatically to
such questions for highly complicated systems and properties.
APPLICATIONS
The technique described here has been applied in a number of real-life
applications, notably in hardware verification and to prove correctness
of a variety of software protocols (see for instance the book on Model Checking by Clarke et al book). In the COSoDIS project
in
particular, we are using model checking as a verification technique for
analysing (legal and electronic) contracts (see link below).
Figures:
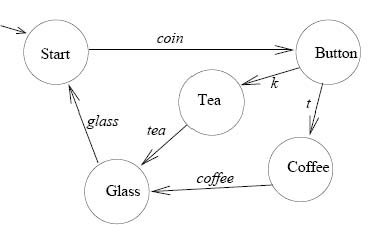
Fig. 1. The automaton of a coffee machine (back to text)
References:
- E.M. Clarke and E.A. Emerson. Design and
synthesis of synchronization
skeletons using branching time temporal logic, In: Proceedings of the
Workshop on Logics of Programs, vol. 131 of LNCS, pages 52-71.
Springer-Verlag, 1981.
- Simson Garfinkel. History's
worst software bugs. (If for some reason the link does not work, I
keep a local copy of the article here.)
- A. Pnueli. The temporal logic of programs.
In: Proceedings of
the 18th IEEE Symposium on the Foundations of Computer Science,
pages 46-57, 1977.
- A.N. Prior. Time
and Modality. Oxford: Clarendon Press, 1957
- J.P. Queille and J. Sifakis. A temporal
logic to deal with fairness in transition systems. In: 23rd Annual Symposium Foundations of
Computer Science, pages 217--225, 1982.
- E.M. Clarke, O. Grumberg and D. Peled. Model Checking. The MIT Press, 1999.
Useful
Links:
Contact address:
Gerardo Schneider
+47 22 85 29 71
gerardo at ifi.uio.no
http://folk.uio.no/gerardo/
