Preparation
Lectures: Thursday, Friday, week 7.
Read: Book Chapter 15.
Basic Exercises
Chapter 15: Problems 15.1, 15.3, 15.4, 15.17 (pizza), 15.26 (BOOKKEEPER).
Exercises
(1.) You roll 2 dice. What is the probability that the two values that turn up are different?
You roll 3 dice. What is the probability that the three values that turn up are all different? What is the probability that there are at least two dice with the same value?
You roll n dice. What is the probability that there are at least two dice with the same value?
(2.) In Holland, license plates on cars have the following structure. They consist of a sequence of three groups of symbols. Each group is either a pair of two letters (from the alphabet A-Z, but not I, O, or Q) or of two digits (from 0-9). How many different license plates are there?
(3.) Given a prime number p. Show that \[ {p \choose k} \] is divisable by p for all \(0 \lt k \lt p\).
Does this also hold when p is not prime?
(4.) How many triples (x,y,z) with x,y,z \(\in \mathbb{N}^+\) are there such that x+y+z = 10? How many are there such that x+y+z=N, for an arbitrary N?
Hint: imagine a chocolate bar with N pieces in a row. In how many ways can you chop it into three pieces of size x, y, and z?
(5.) Given a finite set A = of n elements {1,2,..,n}. How many different binary operators exist on the set A?
(6.) Prove Fermat's little theorem, namely that \[ a^p ≡ a \; (\text{mod}\; p) \] for any prime number p, and any natural number a.
We have actually already proved this in the lecture. This time, do it by induction on a.
Let me help you: The base case (a=0) is easy: 0p ≡ 0 (mod p) for any p > 0.
The step case assumes that kp ≡ k (mod p) (this is the induction hypothesis), and has to show that \[ (k+1)^p ≡ (k+1) \; (\text{mod}\; p) \] Luckily, we have now learned how to expand the expression (k+1)p, which should help you finish the proof.
Hint: Make use of what you learned in exercise 3!
(7.) In the lecture, we used Pascal's triangle to prove that: \[ { n \choose k } + { n \choose k+1 } = { n+1 \choose k+1 } \] Prove the above by using the definition of the choose function ("över") and manipulating the factorials.
(8.) You are taking a course with 54 students (including you). For the exercise sessions, you are randomly divided into 9 groups of size 6. You are secretly in love with one of your classmates (not yourself). What is the probability that the two of you end up in the same group?
(9.) (Inspired by Problem 15.38 in the book.) Use the Pidgeon Hole principle to show each of the following statements. Clearly indicate what the pidgeons are and what the holes are.
a. Given a set of 100 different integer numbers. There must be at least two numbers in the set whose difference is a multiple of 37.
b. Given 5 points within a unit square. There must be at least two points that have a distance at most 1/√2 from each other.
(10.) Given a graph with n nodes: 1, 2, 3, ..., n. How many different undirected graphs can we make from these?
(11.) Given a directed graph that is a bijection. This means that every node has exactly one outgoing arrow, and exactly one ingoing arrow. What is the probability that there is a cycle in the graph?
Starred Exercises
These exercises are for students who are looking for a challenge.
(1*.)
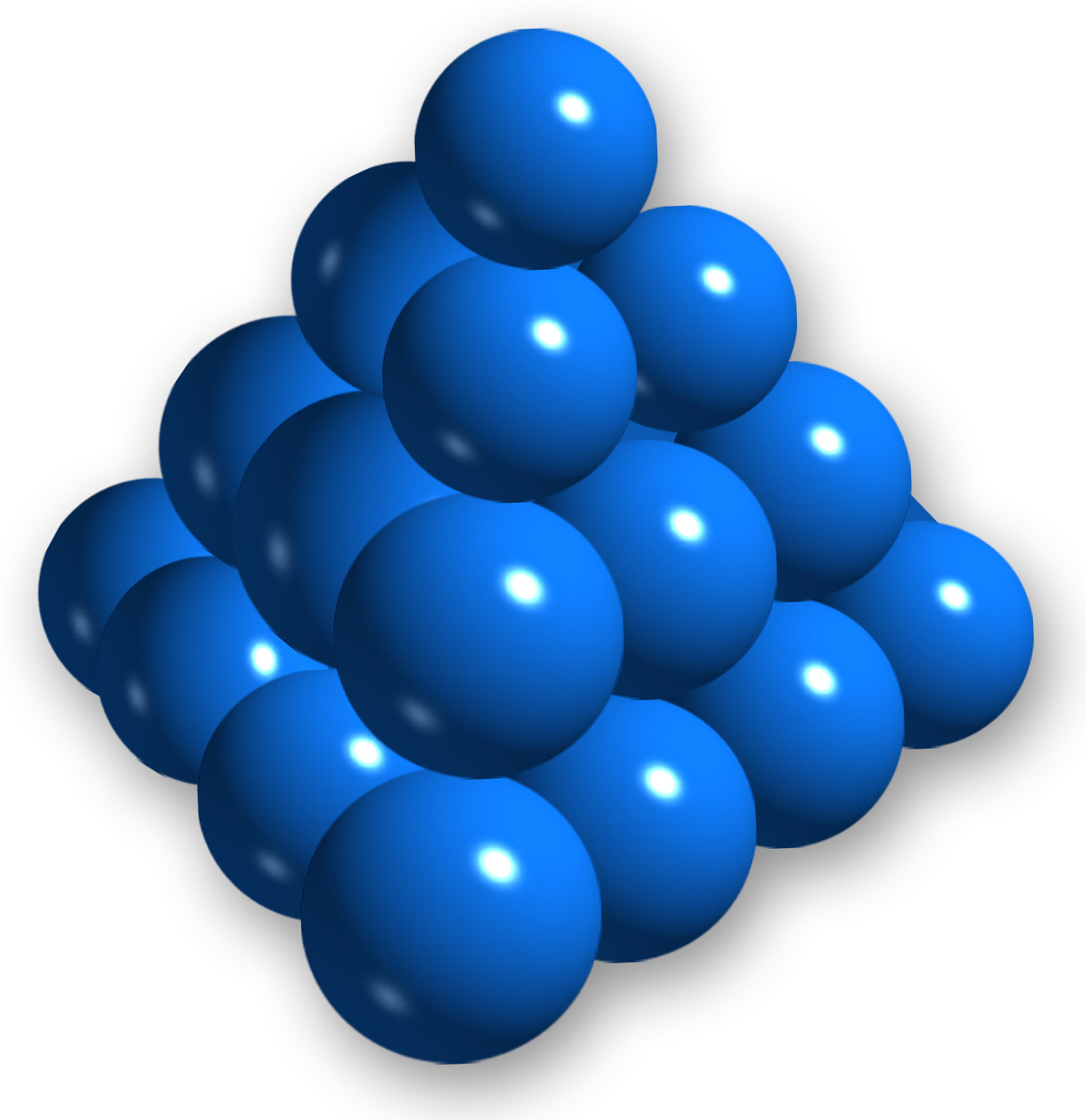
Take a look at the above picture of a triangular pyramid (or, actually, tetraeder) made out of blue marbles. If we express the number of needed marbles as a function of height, we get the following result: For a pyramid of height 1, we need 1 marble. For a pyramid of height 2, we need 1+3=4 marbles. For a pyramid of height 3, we need 1+3+6=10 marbles.
It turns out that the number of marbles for a pyramid of height n is: \[ { n+2 \choose 3 } \] Prove this. (This was wrong in a previous version, now corrected.)
Hint: You can prove this by induction on n. But, you can also prove it directly by trying to associate each marble with a choice of 3 things out of n+2 things... Look at exercise 4 again and use what you learned there.
(2*.) Show that if the audience picks 8 cards from the deck of 52 cards, and the assistant reveals a sequence of 6 cards, the Magician can know the other 2 cards.