When you are done, please submit the URL of your solution using the Fire system

Before you begin: all the material you need for this lab can be found in these Interactive videos Enrollment key: CMDKM-50508. Please try them out (about an hour of material in total), do the in-video quizzes, add insert questions in the videos as you go along (we’ll try to answer the questions!). If university sign-in is not working for this site you will need to create a personal account. Let us know if you can’t get access one way or another!

In this lab assignment, you will use the online system Code.World to draw a simple picture of a chess board, defined as a function chess where chess n (for some non negative integer n) is a drawing of a chess board of size n times n. The expected output of the following program:

program = drawingOf(chess 9)

should give:

The lab is split into two parts, each exercising a different aspect of problem solving with Haskell. Note: Please make sure you follow the submission guidelines when you write your code.

To prepare for the assignment you must have followed the first one-and-a-half lectures of the course. You will need a basic uderstanding of (i) The code.world picture functions (ii) definitions using guards (iii) simple recursive functions, and (iv) simple list comprehensions.

Part 1

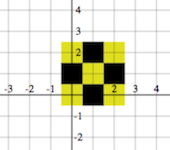
Part 1 this part assignment is broken down into tasks A, B and C described below. The goal of parts A, B and C is to produce the bottom row of a chess-board. On an n by n chess board (OK, n is always 8 in normal chess, but let’s be more general) let us refer to the positions of the squares by their coodinates, so the bottom left corner is position (0,0), and the top right is (n-1,n-1). This picture of drawingOf(coordinatePlane & chess 3) might be useful to see this:

Assignment A

The colour of a square in the bottom row of the board is either white (we will draw it as yellow) or black depending on its position. Let’s say that the first square (on the left) is at position 0 (since it will be displayed at coordinate position (0,0)). This square is always white.

Define a function colourAt which when given a non-negative integer n returns the colour of the square at position n. The colours yellow and black are predefined in code.world. For example, colourAt 2 should give yellow. Try your definition by using the following function:

program  = programA
programA = drawingOf ( coloured(circle 2, colourAt 2) 
                    & coloured(circle 3, colourAt 3) )

Assignment B

Define a function squareAt n which gives a picture of a solid rectangle at position (n,0) on the grid, with the right colour for that position.

Try your function out with:

program  = programB -- edit the previous version of this definition
programB = drawingOf ( squareAt 0 & squareAt 7 & coordinatePlane ) 

You should get the following:

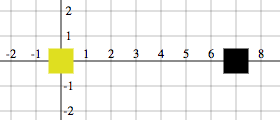
Assignment C

Define a function row, where row n draws the bottom row of an n by n chess board. Use recursion! Hint: think about the simplest possible base case!

Try your function out with

program  = programC
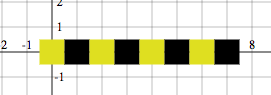
programC = drawingOf (row 8 & coordinatePlane)

You should get the following image:

Part II

Part I was an exercise in using recursion, but for part II (broken down into parts D,E and F) we are going to exercise a different method. To draw a whole board (part F) we are going to define a function to draw a square at a given position, and use a list comprehension to draw the whole board. We will build up the solution in a couple of similar steps to assignments A and B.

Assignment D

Define a function colourAtPos where colourAtPos x y which gives the expected colour of the square at coodinates (x,y) on the board.

To test this, draw a square with the same colour as the top right square of a 8 by 8 chess board (i.e. colourAtPos 7 7).

Assignment E

Define a function squareAtPosition such that squareAtPosition x y gives a picture of the square at coordinates (x,y). For example, this program displays the image below

program = programE
programE = drawingOf (coordinatePlane & squareAtPosition 3 4)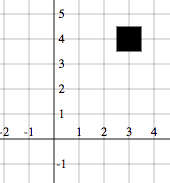

Assignment F

Now you know how to draw the square at a given position, all you need to do to make a picture of a chess board of size n times n is to make a list of pictures, one for each possible position in the board, and join all these pictures together with the code.world function pictures. To do this we won’t use recursion, but instead a list comprehension. Look for examples were we build a list from two lists, such as

[ x+y | x <- [1,2,3], y <- [10,20,30]]
-- try it out in ghci!

Assignment H (Optional)

Can you work out a nice way to draw the whole board using recursion? See if you can solve it without too much “cut-and-paste” code (i.e. there should not be several parts of the program which are very similar).

Submission

This lab has two deadlines:

• First deadline (Wednesday, Sept. 6 at 23:59 2017): You need to have made a serious effort on completing the complete lab assignment.
• Final deadline (Friday, Sept. 15 at 23:59 2017): You need to have gotten a pass on the lab.

After this first lab, all lab deadlines will be on Mondays at 12 noon.

Sign in to code.world (e.g. using a google account) to be able to save your files. When you are done, click on “Share” and copy the URL. Add this as a comment to your submission in the Fire system. Remove irrelevant things from the code.world file.

Before you submit your code, Clean It Up! Remember, submitting clean code is Really Important, and simply the polite thing to do. After you feel you are done, spend some time on cleaning your code; make it simpler, remove unnecessary things (the assignments A-H are not unnecessary, so don’t delete those!), etc. We will reject your solution if it is not clean. Clean code:

• Does not have long lines (< 78 characters)
• Has a consistent layout (do not use TAB characters in your code)
• (Not required for Lab 1) Has type signatures for all top-level functions
• Has good comments where needed
• Has no junk (junk is code that is not needed by the assignments, commented code, unneccessary comments).
• Has no overly complicated function definitions
• Does not contain any repetitive code (copy-and-paste programming)

When you are done, please submit it using the Fire system

This lab will be graded offline. But labs 2 and onwards need to be presented to your grader at specific times shortly after the submission deadlines. Instructions will be provided on the lab overview page.

Good luck!