Discrete Mathematics for Computer Scientists -- Assignment 7

Discrete Mathematics for Computer Scientists -- Assignment 7 - Graphs and Combinatorics

DIT980, HT 2015

Fire | Forum | TimeEdit | Links | 2014

Assignment Week 7 - Graphs and Combinatorics

Assignments

(1.) Given an undirected graph G where every node has a degree ("gradtal") of 2 or more. Show that G cannot be a tree.

Hint 1: Draw some example graphs where every node has degree >= 2 and try to make them look like trees. You will find this is impossible because you will need to draw too many edges. Think about this: What is the minimum number of edges you need to draw for a graph with n nodes in order to make the degree of every node at least 2?

Hint 2: You may use any lemma ("sats") about graphs in the book. Specifically, lemma 7.3 (page 189) and its proof are relevant, and also lemma 7.7 (page 194).

(2.) Take a look at the directed graph below. How many topological orderings are there for this graph? Motivate your answer.

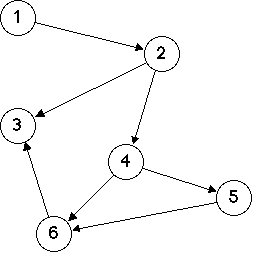
(3.) How many different strings can you form using exactly the 8 letters A, N, A, C, O, N, D, A in any order?

Compute your answer in two different ways: (1) Write a program that enumerates all possibilities, and (2) Show how the answer can be calculated using formulas from combinatorics. Ideally, you should get the same answer :)

Hint: If you write your program in Haskell, use the standard Haskell functions nub and permutations from the module Data.List. Don't forget to import Data.List.

Submission

Submission of this assignment should be done electronically through the Fire system.

The submission deadline is Wednesday, October 21, at 13:00. At this time, you should have submitted a serious attempt to solve the assignment. A serious attempt is either an answer you believe to be correct, or a partial answer plus a detailed explanation of what you have tried to come up with a full answer. An empty document is not a serious attempt.

After submitting, you have until Friday October 30 (midnight, OBS: Friday!) to submit a completely correct version.

You can submit your answers in any of the following formats:

A simple text file, ending in .txt. You can make text files in any text editor, and then upload it to the Fire system.
(When using a text file, you may sometimes need to "invent" notation. Please be clear about what your notation means. A list of suggested notation for text files is provided by us. You may also use Unicode.)
A picture you have made in a painting program, ending in .gif, .jpg, or .png. You can use for example MS Paint, or Google Docs to make a picture, and upload it to the Fire system.
A PDF-file, ending in .pdf. You can make PDF files by for example using OpenOffice, LibreOffice, Microsoft Word, or Google Docs, and choosing export as PDF. Then, upload the PDF-file to the Fire system.
A scanned in document, ending in .pdf or .jpg. You can write your answer on a piece of paper, and use a scanner to scan it in and convert to a PDF-file. Or you can use your mobile phone to take pictures of the papers, and upload these to the Fire system.

If you submit multiple files, please name and/or number them such that the order in which we should read them is obvious. You can also write a text file, and have it refer to pictures that you upload separately.