This is an old website! For the current version, visit: http://www.cse.chalmers.se/edu/course/TIN172/
Note: This document also exists in a PDF version.
Now there are solutions to some of these problems.
This examination consists of 8 basic questions and 4 advanced. There are no points awarded for the questions, but you can either give a correct answer, or fail.
Below are lot more questions, just to get you working. Also, some questions are a bit larger than the corresponding exam question would be. If a question consists of different parts (a), (b), …, then you can assume that one of these parts would constitute an exam question. (Except for the advanced questions).
The number of questions (basic plus advanced) that you need to answer correctly in order to get a certain grade is shown in this table:
| Grade | Basic questions | Advanced questions |
|---|---|---|
| 3 | 6 | — |
| 4 | 7 | 1 |
| 5 | 8 | 3 |
Apart from a pen, you are allowed to bring 1 A4 paper of personal notes.
Calculator will probably not be allowed, simply because it will not be necessary.
This exam covers the following sections from chapters 1–6 and 8–10 in the course book:
Imagine a computer implementation for the following task. Classify your implementation according to the complexity dimensions below. (Note that in some cases you can select more than one value). Also explain why you chose that/those value(s).
This is a personal computer game where the player designs, builds and runs a city with infrastructure, inhabitants, etc.
Assume that the game does not connect to other instances of the same game (over the internet or any other network).
| Dimension | Possible values | Value(s) | Explanation |
|---|---|---|---|
| Modularity | (F)lat / (M)odular / (H)ierarchical | ||
| Representation | (S)tates / (F)eatures / (I)individuals+relations | ||
| Planning horizon | (S)tatic / (F)inite / (I)ndefinite / i(N)finite | ||
| Observability | (F)ull / (P)partial | ||
| Dynamics | (D)eterministic / (S)tochastic | ||
| Preference | achievement (G)oals / (C)omplex preferences | ||
| Number of agents | (S)ingle / (M)ultiple | ||
| Learning | knowledge is (G)iven / learned from (D)ata / learned from (E)xperience | ||
| Computational limits | (P)erfect rationality / (B)ounded rationality |
Here are two possible alternative tasks that the previous question could have been about instead of Sim City:
Note: When you encounter “search algorithm X” below, it could mean any of the following algorithms:
(Note: This exercise is modified from Uni. Berkeley’s CS188x)
Imagine that a car-like agent wishes to exit a maze like the one shown below (where X marks the exit and > is the car). The maze is quite ordinary, except that there might be openings in the outer walls. If the car goes out of an outer wall opening, it will directly enter the maze at the corresponding opeining at the opposite wall.
+----------+-------+
| X | > |
| +--+ | + |
| | | | |
+ +--+ | | +
<== | | | ==>
+--+ | + + +
| | |
+--+ + +-------+
| |
+------------------+The agent is directional and at all times faces some direction d ∈ (N, S, E, W). With a single action, the agent can either move forward one step or turn. The turning actions are left and right, which change the agent’s direction by 90 degrees. Any action that would result in a collision with a wall crashes the agent and is illegal. The agent’s goal is to find a plan which parks it on the exit square using as few actions (time steps) as possible.
(a) If the grid has size M × N, what is the size of the state space? Justify your answer. You should assume that all configurations are reachable from the start state.
(b) What is the maximum (forward) branching factor of this problem? You may assume that illegal actions are simply not returned by the successor function. Briefly justify your answer.
(c) Is the Manhattan distance from the agent’s location to the exit’s location admissible? Why or why not? (The Manhattan distance is described in exercise 3.3b in the course book).
Assume the following search graph:
The start node is green, the goal is blue. The edge costs and the heuristic values are written in the graph. Assume that the neighbors are selected in alphabetical order (unless the cost function doesn’t say otherwise).
Which path will the search algorithm X find first, and what is the resulting path cost?
Use the following search graph instead:
The start node is A, the goal is G, and there is no heuristic function (so best-first and A* are quite useless).
Exercise 3.3 (a, b, c or d) from section 3.10 in the course book.
Consider the A* search problem represented in the following figure, where A is the start node and E is the goal node:
A [3,3]
/ \
/ \2
[5,3] B \
| C [4,2]
| / \
[6,1] D / \
\ / F [6,3]
[3,0] EThe pair [f,h] at each node indicates the value of the functions f (total cost estimation) and h (heuristics) for the path ending at that node.
(a) Given this information, what is the cost of each edge? The cost (A,C) = 2 is given as a hint.
Note: this is a minor trick question – not all edge costs can be inferred from the information.
(b) Is the heuristic function h admissible? Explain why or why not.
Consider a simple three-variable CSP, with variables A, B and C, all having domains {1,2,3,4,5}. The constraints are that A, B and C sum to 7, and that A is smaller than B which is smaller than C.
(a) Draw the constraint graph over the variables A, B and C.
(b) Which values remain in the domains after enforcing arc consistency?
| Variable | Values before AC | Values after AC |
|---|---|---|
| A | {1,2,3,4,5} | |
| B | {1,2,3,4,5} | |
| C | {1,2,3,4,5} |
Exercise 4.5 from section 4.13 in the course book, i.e.:
(a) Draw the constraint graph over the variables A, …, E.
(b) Perform arc consistency on the problem.
(Note: This exercise is borrowed from Uni. Berkeley’s CS188x)
You are in charge of scheduling for computer science classes that meet Mondays, Wednesdays and Fridays. There are 5 classes that meet on these days and 3 professors who will be teaching these classes. You are constrained by the fact that each professor can only teach one class at a time.
The classes are:
The professors are:
(a) Formulate this problem as a CSP in which there is one variable per class. State the domains and constraints. Constraints should be specified formally and precisely.
(b) Draw the constraint graph associated with your CSP.
(c) Perform arc consistency on the problem.
Exercise 5.2(a) from section 5.10 in the course book.
Exercise 5.3 from section 5.10 in the course book.
Exercise 5.4 (a, b or c) from section 5.10 in the course book.
(Note: This exercise is borrowed from Uni. British Columbia CPSC502)
Consider the following knowledge base, where {a, b, c, d, e, f, g, h} is the set of all atoms:
(a) Give a model of the knowledge base.
(b) Give an interpretation that is not a model of the knowledge base.
(c) Give all atoms that are logical consequences of the knowledge base.
(d) Give all atoms that are not logical consequences of the knowledge base.
Fill in the joint probability table so that the binary variables X and Y are independent.
| X | Y | P(X,Y) |
|---|---|---|
| + | + | 3/5 |
| + | – | 1/5 |
| – | + | |
| – | – |
The exercises from “Homework 1 (Probability Recognition)” at Piazza. Questions 1.1, 1.2 and 2.1 can be seen as basic questions.
Note: To sign up for Piazza, click “Sign Up”, then search for Chalmers, then select TIN172. You have to enter your email address and wait for the confirmation mail, as customary nowadays.
(Note: This exercise is borrowed from Uni. British Columbia CPSC502)
A cab was involved in a hit-and-run accident at night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data:
(a) What is the probability that the cab involved in the accident was Blue?
(b) Represent this story as a belief network. Explain all variables and conditional probabilities. What is observed, what is the answer?
Exercise 6.8 (a, b or c) from section 6.8 in the course book.
Note that part (b) is quite large, and a real exam question will not cover such a big network, or only ask you to eliminate one specific variable.
Exercise 8.1(b) from section 8.8 in the course book.
Give the STRIPS representations for the pick up mail and deliver mail actions, as well as for pick up coffee and deliver coffee.
Exercise 8.4(a) from section 8.8 in the course book.
Give the STRIPS representations for the pick up mail and deliver mail actions, as well as for pick up coffee and deliver coffee.
Exercises 1.1, 1.2, 1.3 and 3.1 from “Exercises: A simple Markov decision process” at Piazza.
Exercise 9.13 (a) from section 9.8 in the course book.
(Note: This exercise is borrowed from KU Leuven’s H01O4)
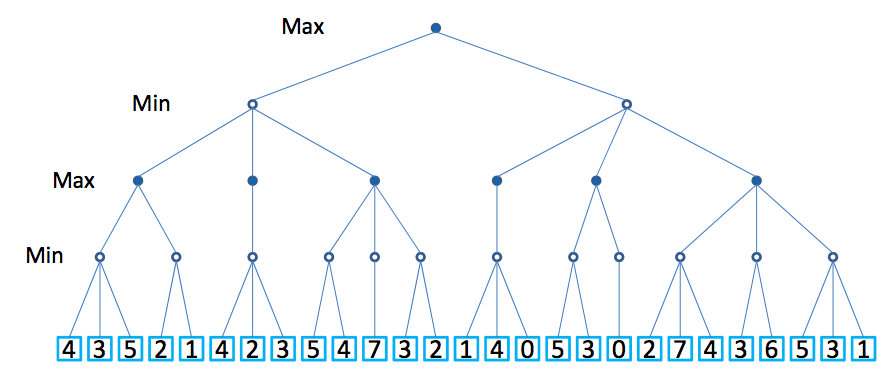
Assume the following two-player game tree:
(a) Perform the minimax algorithm on the game tree, without αβ pruning. Show the final min/max values at each node in the tree.
(b) Perform the minimax algorithm on the game tree, now with αβ pruning. Show the final min/max values at each node in the tree, and which edges are pruned.
Which state will be selected, and how will the resulting search frontier look like after iterations 1, 2 and 3 of the A* algorithm?
Sort the frontier according to the order states will be selected from it!
| Iteration | Selected state | Resulting frontier |
|---|---|---|
| Initial | — | {abc} |
| 1 | ||
| 2 | ||
| 3 |
Assume the following about the problem:
Assuming that the current state is x1 … xn, the following are the possible neighbors:
Assuming that the current state is s and the goal is g:
h(s) = |C(a, s) − C(a, g)| + |C(b, s) − C(b, g)| + |C(c, s) − C(c, g)|
where C(x, y) counts the occurrences of the character x in y.
Also assume that your implementation uses cycle checking, but not multiple path pruning.
Exercise 4.12 from section 4.13 in the course book.
You don’t need to solve the problem, but you have to list each variable together with its domain, and all constraints that the puzzle gives rise to.
Also, draw the corresponding constraint network.
(Note: This exercise is borrowed from Berkeley’s CS188x)
You are a detective in charge of bringing down drug dealers (D). A tip has led you to a small apartment complex where you believe one or more D might be hiding out.
There are five apartments in a row. Each apartment could contain a drug dealer D or could contain innocent people: adults (A), families with babies (B), or with teenagers (T). Before you break down a door, you need to be absolutely sure that a dealer D is inside, otherwise you could get sued for police suboptimality.
1 2 3 4 5
+-----+-----+-----+-----+-----+
| | | | | |
| | | | | |
+-----+-----+-----+-----+-----+
m c r mTo help you narrow down where drug dealers D might be (if any are there at all!), you use the fact that different people make different noises. Every time you walk between two apartments, you can hear the louder of the two noises that are being made in those apartments. The loudest people are teenagers T, who blast music (m), the next loudest are babies B who cry (c), the next loudest is the drug dealer D, who makes a rustling sound (r), and the quietest people are adults A, who are totally silent (s). For example, if there were a baby in one house and a teenager in next, you would hear music (m) when standing between those apartments.
Walking by the five apartments, you hear the noises shown in the diagram above. You decide to try solving this problem as a CSP.
(a) What are the variables and domains in this CSP? (Do not use a formulation where the noises are variables; they’ll show up as constraints.)
(b) Write down the binary and/or unary constraints implied by the noises shown above at the apartment boundaries.
(c) You decide to narrow down your domains by enforcing arc-consistency. What are the remaining domains of each variable after arc consistency is enforced.
(d) List all solutions to this CSP or state that none exist.
(e) Is it ok for you to break into apartment 4? Justify your answer.
This is a continuation of the basic weather forecasts question.
Questions 2.2 and 3.1 from the Homework 1 at Piazza can be seen as advanced questions.
This is a continuation of the basic taxi question.
(c) Suppose there were three independent witnesses, two of which claimed the cab was Blue and one of whom claimed the cab was Green. Show the corresponding belief network. What is the probability the cab was Blue?
(d) Suppose it was found that the two witnesses who claimed the cab was Blue were not independent, but there was a 60% chance they colluded. Show the corresponding belief network, and the relevant probabilities. What is the probability that the cab is Blue?
(Note: This exercise is borrowed from Uni. Berkeley’s CS188x)
You are playing a simplified game of Wheel of Fortune. The objective is to correctly guess a three letter word. Let X, Y, and Z represent the first, second, and third letters of the word, respectively. There are only 8 possible words: X can take on the values ‘c’ or ‘l’, Y can be ‘a’ or ‘o’, and Z can be ‘b’ or ‘t’.
Before you guess the word, two of the three letters will be revealed to you. In the first round of the game, you choose one of X, Y or Z to be revealed. In the second round, you choose one of the remaining two letters to be revealed. In the third round, you guess the word. If you guess correctly, you win. The utility of winning is 1, while the utility of losing is 0.
You watch the game a lot and determine that the eight possible words occur with the probabilities shown below. Your goal is to act in such a way as to maximize your chances of winning (and thereby your expected utility).
| X | Y | Z | P(X,Y,Z) |
|---|---|---|---|
| c | a | b | 0.10 |
| c | a | t | 0.10 |
| c | o | b | 0.20 |
| c | o | t | 0.20 |
| l | a | b | 0.05 |
| l | a | t | 0.15 |
| l | o | b | 0.05 |
| l | o | t | 0.15 |
(a) What is the distribution P(Y, Z)? Your answer should be in the form of a table.
(b) Are the second and third letters (Y and Z) independent? Show a specific computation that supports your claim.
(c) Are the second and third letters (Y and Z) independent if you know the value of the first letter (X)? Show a specific computation that supports your claim.
(d) Suppose that in the first round, you ask about X and are told that X = c. It is the second round and you can now either ask the host to reveal Y or to reveal Z. If you ask the host to reveal Y, what is the probability that you will win in the third round?
(e) What letter should you ask the host about in the second round to maximize your chance of winning, Y or Z?
(f) What is your expected utility if you act optimally from the state where X=c?