| Software Engineering using Formal Methods | ||||||||||
|
Exercises Week 3 - Channels and Linear Temporal Logic |
||||||||||
|
These are the exercises for week 3. During the exercise session we will try look at 1, 2, 3, 5a, 5c, 6c, 8, 9.1, 9.2, 10.1, 10.3, 11.1 and 11.3. ChannelsThe solutions to exercises 1 -- 4 can be found here. Exercise 1Channels are useful when modelling distributed systems. In Promela a channel has a capacity and a message type.
chan myChan = [0] of { byte }
This simple example specifies a channel called myChan with 0 capacity, making it a rendezvous channel. The messagetype in this case is byte. Now create two processes. The first process sends the numbers 0 through 9 onto the channel. The second process reads the values of the channel and outputs them. Exercise 2Is it possible that process p does not read from the channel at all ? chan com = [0] of {byte} byte value = 0; proctype p() { byte i = 0; do :: if :: i >= 5 -> break :: else -> printf("Doing something else\n"); i ++ fi :: com ? value ; printf("p received: %d\n",value) od } init { atomic { run p() } end: com ! 100; } Exercise 3Model a system having 5 clients and 2 servers where a client cannot send another request before his previous one was processed by a server. The suggested solution uses buffered channels and describes the behaviour of the server processes. Complete the solution for the client processes. chan request = [2] of { byte, chan}; chan reply[5] = [2] of { byte }; active [2] proctype Server() { byte client; chan replyChannel; do :: request ? client, replyChannel -> printf("Client %d processed by server %d\n", client, _pid); replyChannel ! _pid od } proctype Client(byte id) { ... } init { ... } Exercise 4Model an office where two computer systems are hooked up to a single printer. Model the computer systems such that they have mutual exclusion on the printer. The printer can be modeled as the number of jobs it has. The two systems can communicate with each other via a rendezvous channel. Verify that it is never the case that both systems print at the same time. Exercise 5For each formula, F, find an interpretation, I, of the propositional variables such that val_I(F) = T
Example
5a
5b
5c
Exercise 6Are the following formulas satisfiable. If they are, show a satisfying interpretation:
6a
6b
6c
Exercise 7Formalize in propositional logic: In earlier times there existed an island whose inhabitants were either knights or knaves. A knight always tells the truth, while a knave always lies. Hedwig and Katrin lived on that Island. A historian found in the archives the following statements: Hedwig: I am a knave if and only iff Katrin is a knave. Katrin: We are of different kind. (after Raymond Smullyan, Knights and Knaves) Answer: H : Hedwig is a knight, K : Katrin is a knight H <-> (!H <-> !K) K <-> !(H <-> K)
Exercise 8Formalize in linear temporal logic: If a request occurs, then either it will eventually be acknowledged, or the requesting process will not ever be able to make progress. (Hint: Fix first a vocabulary (propositional variables) and express then the property in terms of the chosen vocabulary.)Answer: R : request is made, A : request is acknowledged R->(<>A||[]!A)
Exercise 9Consider a crossing of two streets with one traffic light (nr 1) controlling the north-to-south direction and one (nr 2) for the west-to-east direction. Assume you have the following propositional variables: R1 (traffic light 1 is red), G1 (traffic light 1 is green), R2 (traffic light 2 is red), G2 (traffic light 2 is green) Give LTL formulas formalising the following properties:
Answer :
Exercise 10Don't despair if you had an hard time understanding the procedure to obtain an automaton. As you saw in the lectures, algorithms for getting one out of a LTL formula are not straightforward. There are some tools that can be used to check your own solutions. You can try the tool GOAL: GOAL homepage With this tool you can
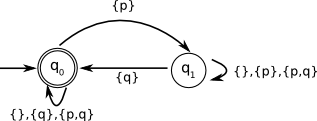
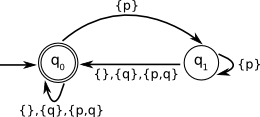
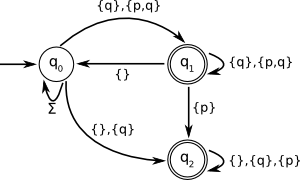
IMPORTANT NOTE: the program has a different way to label the transitions. Refer to the documentation (Help -> Help contents) to understand in what they differ. MORE IMPORTANT NOTE: As a consequence of the previous note, if in the exam a similar exercise occurs, Which language is accepted by the following Büchi automata?
Exercise 11Consider the following LTL formulas and their corresponding Büchi automata. State whether these formulas accept the same language or not. If not, provide a counter-example in the form of a word which is accepted by the LTL formula but not by the automaton, or vice versa.
Exercise 12Consider the language formed with the Vocabulary V = {a, b, c}, such that for each word of the language the following holds:
Answer: 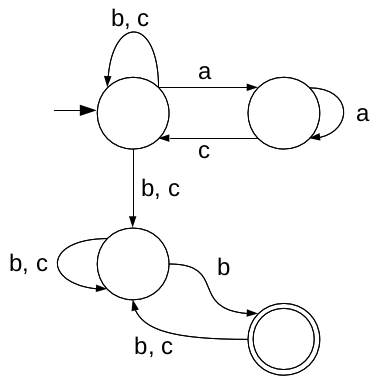
| ||||||||||
| Home | Schedule | Exercises | Labs | Exam | Links | Course | Bart van Delft, Sep 21, 2012 | |||||||||
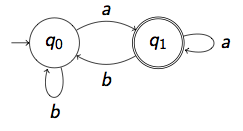 Answer : (b*a)w
Answer : (b*a)w
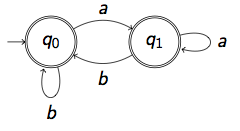 Answer : (a+b)w
Answer : (a+b)w
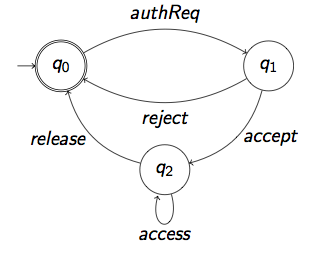 Answer : (authReq (reject + accept access* release))w
Answer : (authReq (reject + accept access* release))w