Lab 3 del 2
Sekantmetoden

Anvisningar:

Skriv först ett program med något slutvillkor, nästan vilket som helst, så du får nåt som kan köras och arbeta sedan med slutvillkoret.
Själva rekursionen är inte så svår här, det är dock lätt att få till ett slutvillkor (iterativt såväl som rekursivt) som bara är nästan rätt och det är svårigheterna att hitta på bra testfall som är svårt .

Själva sekantmetodklassen ca15 rader + testprogram som kan bli långt. Mitt är 250 rader, ganska mycket längre än metoden det testar.

(och som vanligt är det viktigt att de namn vi ger verkligen används så våra automatiska test fungerar.)

Förkunskaper:

Den här uppgiften kräver framförallt kunskap om rekursion men även funktionsparametrar och interface. Efter föreläsning 10 har vi täckt det.
På övningen om rekursion gås också igenom ett exempel (integrera) som kan vara bra att ha gjort. (Övning 4)
Det är inte heller fel om man har lite matematisk mognad när man skall hitta testfunktioner.

Syfte:

Att öva på rekursion, funktionsparametrar och interface.
Att öva på att skriva testprogram för sina program.
Och, inte minst, att visa att det är lätt att skriva program som fungerar ofta dvs i det här fallet för många funktioner, men svårt att skriva korrekta program som fungerar för alla funktioner.

Inlämning

Du lämnar in klassen Secant och ditt testprogram (som det såg ut innan du tittade på vårt testprogram). I readme filen lämnar du in utskriften från vårt testprogram ( med variabeln "verbose" satt till värdet 1 som är default så ändrar du inget så blir det så, se början på testprogrammet).

Uppgift:

En välkänd algoritm för att hitta rötter till funktioner är sekantmetoden, du skall implementera följande variant ev den. Den baseras på att man känner funktionsvärdet i två punkter på vardera sidan om roten, a och b i figuren nedan, och sedan drar en linje som förenar funktionsvärdet i dessa punkter. Om funktionen uppför sig väl tex är växande som i figuren nedan eller avtagande, kommer punkten (x) där linjen (dvs sekanten) korsar x-axeln att ligga närmare roten än någon av de ursprungliga punkterna.
Man använder då denna nya punkt tillsammans med den av de andra punkterna (a eller b) som ligger på andra sidan nollstället och ritar en ny linje. I figuren använder man alltså x och b som nya punkter. Detta upprepas tills man är tillräckligt nära nollstället.
Svårigheten består i att hitta ett bra slutvillkor och i att avgöra vilken av a eller b man skall ersätta med x värdet. I figuren ser man direkt att x och b är det riktiga valet men datorn ser ju inga figurer.

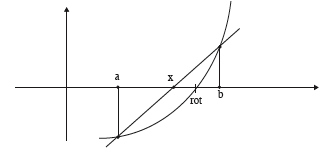
Givet är alltså en funktion f(x) om vilken man vet att
   f(a) <= 0 och f(b) >= 0, a<b och f är växande i intervallet a..b eller att
   f(a) >= 0 och f(b) <= 0, a<b och f är avtagande i intervallet a..b.
   ( f(a) och f(b) får dock inte vara =0 samtidigt)
Det betyder att funktionen någonstans mellan a och b passerar x-axeln dvs dess funktionsvärde är lika med noll.
OBS: Använd sambanden ovan för att hitta nollstället och för att bestämma vilket delintervall som skall användas.
Tips: Om man multiplicerar två tal med varandra så bli resultatet negativt om ett och endast ett av talen är negativt...

Du skall skriva en klass, kalla den Secant, (med c) med en rekursiv binäralgoritm, (en binäralgoritm är en algoritm där man "delar i 2 delar och slänger den ena" men säger egentligen inget om hur stora delarna är. Binärsökning är en speciell binäralgoritm som vi pratat om på föreläsning)

public static double secant(Function f, double low, double high, double eps)

som bestämmer nollstället till den givna funktionen f som finns i klassen f. (Ja bägge heter f) Felet (i x-led) skall vara mindre än eps. Dvs att om x är det verkliga nollstället så skall du svara med ett tal i intervallet x-eps..x+eps.
Funktionen (metoden), f, kommer naturligtvis paketerad i en klass (som även den heter f se ovan och nedan) som uppfyller interfacet Funktion (man kan inte skicka funktioner som parametrar men klasser går bra) 

public interface Function {
    public double f(double x);
    public String toString(); //egentligen brukar man inte ha med toString i interface
}

Du måste också implementera en tostring() metod i klassen som implementerar interfacet.
Det kan också vara lämpligt att i f testa orimliga anrop tex om f är log n och man anropar med 0 som argument.

Skriv också en klass med ett huvudprogram som testar secant med olika funktioner och skriver ut resultatet tex enligt:

OK: "x*x-0.6" : +/-0.774596 = 0.7745966691655485 # (0.0..5.0) #

Här skriver jag ut hur det gick (OK), funktionen som testas, ett kolon, rätt svar (två rötter här), ett likhetstecken, svaret från din secant metod, intervallet, och ev. kommentarer. Se också längst ner på sidan. Observera att jag lagt in rätt svar i toString metoden vilket jag tyckte var finurligt. Rätt svar kan man tex få från Wolframs hemsida.

Man kan beräkna en ny punkt enligt formeln:

Tips:

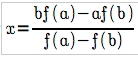
Igen: Om man multiplicerar två tal med varandra så bli resultatet negativt om ett och endast ett av talen är negativt...

Det enda svåra här är att få till ett bra slutvillkor! Använd tipset ovan.

Förslag på några fler funktioner att testa: (observera att funktionen ovan är en "snäll" funktion som funkar med de flesta program. Funktionerna nedan är mycket tuffare och vi kommer att provköra med dom, funkar inte ditt program får du ju retur och dålig poäng så pröva dessa också)
(jag är inte 100 på att alla uppfyller "f(a) < 0 och f(b) > 0, a<b och f är växande i intervallet a..b" ens för några a och b så blir det fel kan ni ju kolla det först och banna mig sen :-))

10-16 * x2-10-17
x2-2
x3-x2+2x
(x+10)2-0.6
ln(x)
arctan(x)
x-2*10-16
sin(x)-(x/2)*(x/2)

Vill man se hur funktionerna ser ut kan man surfa till wolframsalphas hemsida
http://www.wolframalpha.com/
Skriv "plot function x*x-0.6" i sökrutan så plottas funktionen upp och man kan se ungefär var rötterna finns.
Har man mac så finns det ett verktyg i Program->Verktygsprogram->Grapher som kan göra detta och som också kan beräkna rötterna.

Vanligen har man alltså funktionen (tex x*x-0.6) i en egen klass. Sedan skapar man ett klassobjekt med
Function f = new X2(); // om klassen med x*x-0.6 heter X2
När man testar blir det kanske lite bökigt med många funktioner/många filer och då kan man använda följande programskal om man vill. Vi har inte gått igenom den här typen av deklarationer där man deklarerar klassen direkt efter "new" och kommer inte att göra det, men det underlättar testningen. (och dessutom gör "new" på ett interface som jag nog sagt inte går! Men detta är ett specialfall.) 

public class TestaSecant {
    public static void main(String[] args) {
        Function f;
        double eps = 0.0000000001;
        System.out.println("=======================================");
        System.out.println("ev överskrift");
        System.out.println("-----------------------------------------------");
        f = new Function() {
            public double f(double x){return 3*x-6;}
            public String toString() {return "\"3x-6\" \t\t:         2.0";}
        };
        testFunction(f, eps, 0, 5, "");
        testFunction(f, eps, 3, 5, "!!!! roten utanför intervallet");
        ...
        f = new Function() {...

    }

    private static void testFunction(Function f, double eps, double low, double high, String str) {
        ...
    }
}
Glöm inte kommentera vad du testar.

Vårt testprogram

I slutet på andra veckan kommer ni kanske att få det testprogram som vi kommer att köra för att testa om era labbar fungerar. Det skall ni i så fall köra. Men ni skall göra ert eget testprogram färdigt innan ni tittar på vårt.

Maila gärna oklarheter till mej nu så kan du med gott samvete klaga på kursenkäten sedan :.-)

Alla mail som resulterar i ändringar eller förtydliganden dyker också upp här nedan: