I denna laboration ska ni definiera ett litet bibliotek för att generera musik som kan avlyssnas med vanliga musikprogram. Tiden medger inte något omfattande bibliotek, så den musik vi kan åstadkomma är begränsad; här är ett exempel.
Observera att labben utnyttjar fält (eng,
Viktigt om ljud till er dator. Datorerna i våra labbsalar har av lättförståeliga skäl högtalarna avstängda. För att kunna höra något ljud från dessa datorer måste man ha ett par hörlurar med 3.5 mm-jack av den typ som används till mp3-spelare och liknande. Det är vår förhoppning att ni alla har tillgång till sådana. Om ni gör labben på egen dator har ni förmodligen inte detta problem utan kan avnjuta musiken ur högtalarna. Om ni sitter i labbsalen bör ni koppla in era hörlurar, dubbelklicka på länken ovan och kontrollera att ni kan höra exemplet.
Slutresultatet av ert arbete med denna labb kommer att vara en biblioteksklass med fem funktioner på tillsammans några tiotal rader, så det är inte mycket kod som ska skrivas. Samtliga funktioner arbetar med fält (eng. arrays), som introduceras på föreläsningen på fredag. Labben ska redovisas för en handledare i labbsalen på onsdag 30 januari.
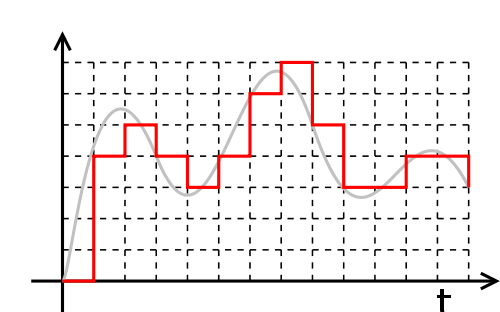
Ljud uppstår genom att en tryckvåg fortplantas genom luften; vi har alltså ett analogt fenomen. För behandling i datorer vill vi ha en digital representation av den analoga signalen. Vi betraktar följande figur (från Wikipedias artikel Digital audio).

Den grå analoga signalen har samplats (avlästs) vid diskreta tidpunkter (de vertikala streckade linjerna). Dessutom har signalvärdena (amplituderna) vid dessa tidpunkter avrundats till närmaste heltalsvärde, representerat av de horisontella streckade linjerna. Den samplade digitala signalen är alltså i detta fall
[0, 4, 5, 4, 3, 4, 6, 7, 5, 3, 3, 4, 4, 3].
En vanlig standard för digital musik är den som används för CD-skivor, där samplingsfrekvensen (dvs antalet avläsningar av signalen per sekund) är 44100 Hz. Noggrannheten i amplitud är typiskt 16 bitar, dvs 216=65536 olika amplituder kan anges. I vårt bibliotek ska vi sampla signaler med denna frekvens, men representera amplituder med värden av typen double, skalade så att amplituden alltid ligger mellan -1 och 1. Först i sista steget, i en klass som ni får given, gör vi om till 16 bitars värden för amplituden. En lämplig datatyp för musik är alltså ett fält av flyttal, dvs double[].
Vi kan göra två observationer:
För högre frekvenser blir förstås upplösningen mycket sämre, men för hörbara signaler har man ändå minst två avläsningar per period. Detta är ingen slump; kommande kurser i signalbehandling förklarar varför man vill ha minst detta antal.
Ladda ner lab2.zip till er katalog för denna kurs (den katalog som också innehåller underkatalogen lab1). Öppna ett terminalfönster och placera er i denna katalog. Gör nu följande:
> unzip lab2.zip inflating: lab2.html ... < mer utskrifter om innehållet i arkivet > ... > ls lab2 Main.java Song.java SoundDevice.java doc elise.txt > cd lab2 > javac *.java
Det första kommandot packar upp arkivet lab2.zip som innehåller bland annat tre .java-filer. Därefter flyttar vi oss till denna katalog och kompilerar javaklasserna.
Härnäst ska ni bekanta er med det givna programmet:
> java Main
Ni hör en ren sinussignal med frekvensen 440 hz i två sekunder, följt av en lika lång signal en oktav högre.
import java.io.File;
public class Main {
// Create sine tone with frequency freq that
// lasts for duration seconds.
public static double[] sine(double freq, double duration) {
int n = (int)(duration*SoundDevice.SAMPLING_RATE);
double[] a = new double[n];
double dx = 2*Math.PI*freq/SoundDevice.SAMPLING_RATE;
for (int i = 0; i < n; i++) {
a[i] = Math.sin(i * dx);
}
return a;
}
public static void main(String[] args) {
SoundDevice device = new SoundDevice();
Song song = new Song(5);
song.add(sine(440,2));
song.add(sine(880,2));
song.play(device);
song.save(device.getFormat(),new File("twotones.wav"));
System.exit(0);
}
}
Vi börjar med att titta på main. Här finns flera saker som vi inte talat om och som introduceras i föreläsning 3. Vi kan ändå läsa och försöka förstå.
Först skapas två objekt, en SoundDevice och en Song (new betyder alltid att man skapar objekt). Vi vet inte riktigt vad det är i Java, men orden bör ändå ge vissa associationer:
Vi är nu i en vanlig situation. Vi har fått ett program, provkört det, tittat på det och förstår en del av vad som pågår. Men en del är fortfarande konstigt. Vad betyder till exempel 5 i new Song(5)?
För denna labb behöver vi inte förstå hur klasserna SoundDevice och Song är uppbyggda. Det räcker att se att konstanten SAMPLING_RATE = 44100 definieras i denna klass.
Den funktion vi ska sampla är s(t) = sin(2π f · t), där f är frekvensen (som heter freq i programmet; i programmering använder man oftast längre variabelnamn än i matematik). Ska vi fylla fältet a med SAMPLING_RATE avläsningar av denna funktion så bör elementet med nummer i vara s(i/SAMPLING_RATE), eller sin(i · dx), där dx definieras som i koden ovan.
Så är det dags för er första programmeringsuppgift; att skapa ett musikaliskt intressantare ljud än en ren sinuston. Er uppgift är att definiera en funktion pluck med signaturen
public static double[] pluck(double freq, double duration) {
som genererar en ton med den givna frekvensen och varaktigheten och som liknar ljudet då man knäpper på en sträng på ett stränginstrument. För detta finns en berömd metod: Karplus-Strongs algoritm, uppfunnen för cirka 30 år sedan. Notera att pluck har samma parametrar som sine, dvs tonens frekvens och varaktighet. Trots det kommer den att låta annorlunda.
Börja med att skapa en ny klass MusicUtils (i en ny fil MusicUtils.java). Flytta dit sine från Main; er nya klass kommer snart att innehålla två funktioner för att skapa två olika ljud. När ni flyttat bort sine från klassen Main måste ni ändra användningen av den i metoden main; ni måste nu skriva MusicUtils.sine för att java-kompilatorn ska hitta metoden. Gör det, kompilera om och kolla att ni fortfarande kan köra Main och höra de två sinustonerna.
Ni ska nu lägga till pluck till den nya klassen. Karplus-Strongs algoritm fungerar på följande sätt:
Först måste ni deklarera och skapa ett fält av flyttal av lämplig storlek på precis samma sätt som i funktionen sine.
Sedan ska ni fylla ni fältets element med värden. Detta görs i två steg:
Testa er funktion genom att ändra i main så att ni anropar pluck i stället för sine (de har precis samma parametrar, så man kan byta ut den ena mot den andra). Ni bör fortfarande höra två toner, men nu ska de låta som när man knäpper på en sträng.
Vi kan nu se att koden i sine och pluck har samma struktur: vi deklarerar och skapar ett fält, fyller det med innehåll och returnerar det. Innehållet blir olika i de två fallen och vi får därför olika ljud när vi spelar upp filen.
Hittills har vi angett toner genom att ge frekvens och varaktighet. Vi vill nu närma oss hur toner anges normalt i musik, dvs med noter i en skala. Vi kan inte gå igenom musikteori här, men nöjer oss med att konstatera att på till exempel en pianoklaviatur finns tolv tangenter per oktav, sju vita och fem svarta:

Vi ska ange toner inte med de vanliga bokstäverna CDEFGAH, eftersom det kräver förtecken för de svarta tonerna och dessutom något sätt att ange oktav; i stället numrerar vi tonerna med heltal som på klaviaturen ovan, där ettstrukna A ges nummer 0 (vi väljer A som utgångspunkt, eftersom den, med frekvensen 440 Hz, oftast är referenspunkt för musikaliska skalor). Ettstrukna C är alltså -9, tvåstrukna C är 3, trestrukna C är 15, osv. Detta har också fördelen att vi lätt får en direkt formel för frekvensen för en given ton: ton nummer k har frekvensen 440*2k/12 Hz. Ettstrukna C har alltså frekvensen 440*2-9/12=261.63 Hz.
Er uppgift är nu att till MusicUtils lägga ytterligare en funktion
static double[] note(int pitch, double duration)
som genererar en ton med givet nummer och varaktighet. Observera: Det enda man behöver göra är att räkna ut frekvensen från tonens nummer, anropa pluck för att få ett fält och returnera detta fält. I note ska man varken skapa eller fylla fältet; det sköter pluck om. Ytterligare en funktion i Math är användbar för att beräkna "2 upphöjt till x".
När ni gjort detta kan ni testa resultatet genom att ändra i main så att programmet spelar till exempel början på Gubben Noak:
song.add(MusicUtils.note(-9,0.4)); song.add(MusicUtils.note(-9,0.4)); song.add(MusicUtils.note(-9,0.4)); song.add(MusicUtils.note(-5,0.4)); song.add(MusicUtils.note(-7,0.4)); song.add(MusicUtils.note(-7,0.4)); song.add(MusicUtils.note(-7,0.4)); song.add(MusicUtils.note(-4,0.4)); song.add(MusicUtils.note(-5,0.4)); song.add(MusicUtils.note(-5,0.4)); song.add(MusicUtils.note(-7,0.4)); song.add(MusicUtils.note(-7,0.4)); song.add(MusicUtils.note(-9,1)); song.play(device);
Valet av 0.4 sekunder per ton här är en smaksak; ni kan välja annat tempo om ni så önskar. Vi ser också att det blir mycket omständigt att beskriva musik på detta sätt. Men innan vi (som en frivillig uppgift) ger oss på att åtgärda detta ska vi förbättra ljudet ytterligare.
Ett betydligt intressantare ljud får vi om vi samtidigt spelar flera toner. Som ett första steg ska ni skriva en funktion
public static double[] average(double[] t1, double[] t2)
som genererar ett medelvärde av tonerna t1 och t2. Vi förutsätter också att de två tonerna har samma varaktighet så att fälten är lika långa. Funktion average ska helt enkelt skapa ett nytt fält och för varje index ta medelvärdet av motsvarande värden i t1 och t2. Definiera funktionen.
Som sista obligatoriska uppgift ska ni definiera en funktion
public static double[] harmonic(int pitch, double duration)
som skapar en ton med givet nummer och varaktighet genom att blanda tre toner som skapats med note, nämligen tonerna med nummer pitch, pitch-12 och pitch+12 (dvs också de två tonerna en oktav under och över den avsedda). Förslagsvis blandas först de två sistnämnda tonerna med average och sedan blandas resultatet med den första tonen, återigen med average.
Slutligen kan ni testa resultatet genom att i main ersätta alla note med harmonic.
När ni kommit så här långt har ni definierat en biblioteksklass MusicUtils som innehåller fem funktioner; sine som ni fick given samt pluck, note, average och harmonic som ni definierat själva. Ni är därmed klara med labben om ni inte vill fortsätta med nästa, frivilliga, uppgift.
I main ovan var beskrivningen av Gubben Noak en del av programmet. Mycket bättre är att spara beskrivningen av sången i en fil noak.txt som börjar
-9 0.4 -9 0.4 -9 0.4 -5 0.4 -7 0.4 -7 0.4 -7 0.4 -4 0.4 -5 0.4 -5 0.4 -7 0.4 -7 0.4 -9 0.4
och sedan låta programmet läsa denna fil och med hjälp av informationen i varje rad skapa en ton som läggs till sången. Ännu bättre är kanske att ändra varaktigheten för tonerna i filen till 0.25, svarande mot en kvartston, och sedan separat ange tempot.
Ändra nu Main så att den läser en sångbeskrivning som ovanstående från standard input, bygger upp en sång och spelar den. Om man har beskrivningen i en fil kan man ändå använda programmet genom att omdirigera standard input:
java Main < noak.txt
I er katalog finns också en fil elise.txt som ni kan använda för testning, om ni inte vill skriva en egen fil för någon musik ni föredrar. Denna fil utnyttjar ovan antydda förbättring; varaktigheten 0.125 betyder en åttondelston. Om man låter detta vara synonymt med varaktigheten hos tonen i sekunder så blir det alldeles för högt tempo. Om en åttondel varar i 0.125 sekunder så hinner man 240 fjärdedelsnoter på en minut; 148 fjärdedelar per minut är mer lagom. En möjlighet är att ange tempot på kommandoraden, så att man spelar stycket på följande sätt:
java Main 148 < elise.txt
Denna uppgift är lätt att göra när man väl lärt sig hur man läser tal från standard input. Detta görs med hjälp av standardklassen Scanner, som kommer att diskuteras på föreläsningen på tisdag i vecka 2. Den som kommit hit innan dess kan läsa i avsnitt 11.1.5 i Ecks bok, söka på nätet eller fråga handledarna.
Förhoppningsvis har ni nu lärt er en del programmering med fält och en del om digital audio. Vi vill bara avslutningsvis påpeka att vi i ett avseende gjort det enkelt för oss: vi har slösat med minne. Vi skapar många och långa fält också för korta ljudsekvenser, och det går att göra det vi gjort och mer med mycket mindre minneskonsumtion. För ett allvarligt menat musikprogram måste man vara mer ekonomisk, men för vårt syfte här lämpar sig en mer frikostig attityd till minnesförbrukning bättre.