Avsikt
Avsikten med denna laboration är att du skall få övning i att konstruera och implementera (skriva program för) en icke-trivial algoritm.
OBS: Du måste använda dig av det du lärt dig under datorintron tex loopar och villkorssatser.

Bakgrund
Ett primtal är ett heltal som inte går att dela jämnt med några andra tal än med 1 och med sig själv. (Notera att med denna definition betraktas även talet 2 som ett primtal.) Den s.k. Goldbach hypotesen säger att varje jämnt naturligt tal (utom 2) går att skriva som summan av två primtal. Det gäller t.ex. att 4=2+2, 6=3+3, 8=5+3, 10=5+5 och 12=5+7. Hypotesen ställdes upp i mitten av 1700-talet och anses allmänt vara sann. Den är dock ännu ej bevisad.

Uppgift
Uppgiften är att skriva ett fristående Javaprogram som kommunicerar med användaren genom terminalen. Programmet skall upprepade gånger fråga efter ett tal. Om talet är jämnt och större än 2 skall programmet visa alla möjliga kombinationer av två primtal som bildar talets summa. Varje kombination av primtal skall endast visas ut en gång. Om t.ex. talet 14 läses in, så skall programmet endast visa ett av primtalsparen (3,11) och (11,3). Om ett inläst tal är <= 2 eller udda skall programmet ge en felutskrift. Körningen ska avslutas när användaren fyller i talet 0. Programmet behöver inte hantera problem när användaren fyller i annat än heltal. Ett exempel på hur det kan se ut när man kör programmet visas nedan:

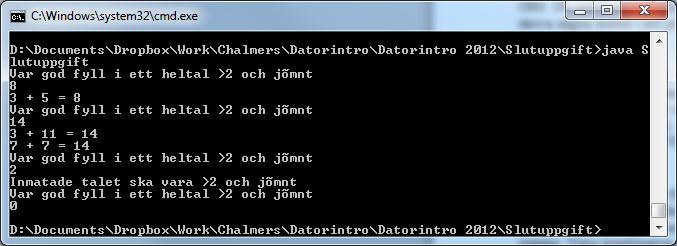
Några tips
Ett enkelt sätt att undersöka om ett viss tal n är ett primtal är att försöka dividera n med alla tal som är mindre än n. Om divisionen går jämnt ut för något av dessa tal så är inte n ett primtal. (Det finns smartare och snabbare sätt att göra primtalstester på, men det krävs inte på denna laboration.)

Viktigt
Inlämningsdatum: 30 augusti senast kl 19.Du lämnar in din uppgift genom att helt enkelt köra programmet och visa upp koden för oss under någon av övningstimmarna..
OBS! Kommentera koden så att du vet vad du har gjort.
Uppgiften får göras och lämnas i grupper av max 2 personer, men observera att båda personerna är ansvariga för hela inlämningen.