Book: 2.8.2, 4.1 - 4.3
Although lexing is the first compiler phase, we don't start from it.
Instead, we start from the middle, abstract syntax, which is
This lecture: how syntax rules look like.
Next lecture: how to write a grammar to generate a compiler front end.
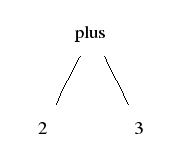
Abstract syntax: what are the significant parts of the expression?
Example: a sum expression has its two operand expressions as its significant parts

Concrete syntaz: what does the expression look like?
Example: the same sum expression can look in different ways:
2 + 3 -- infix
(+ 2 3) -- prefix
(2 3 +) -- postfix
bipush 2 -- JVM
bipush 3
iadd
the sum of 2 and 3 -- English
Parse tree (left): show the concrete syntax (how tokens are grouped together)
Abstract tree (right): show the semantically significant structure
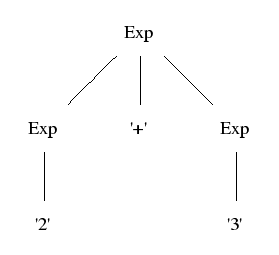  |
Parse tree:
Abstract tree:
  |
Parse trees are defined by context-free grammars
Exp ::= Exp "+" Exp ;
Exp ::= "2" ;
Exp ::= "3" ;
Abstract trees are defined by constructor type signatures
plus : (Exp, Exp) -> Exp
2 : Exp
3 : Exp
1. Give a name (= label) to each rule:
Exp ::= Exp "+" Exp ==> plus. Exp ::= Exp "+" Exp
2. Ignore terminals (= tokens, in quotes):
plus .Exp ::= Exp "+" Exp ==> plus. Exp ::= Exp Exp
3. Treat label as constructor name, LHS (left-hand-side) as value type, RHS as argument types:
plus. Exp ::= Exp Exp ==> plus : (Exp, Exp) -> Exp
One abstract syntax tree can have infinitely many concrete syntax representations.
2 + 3 -- infix
(+ 2 3) -- prefix
(2 3 +) -- postfix
bipush 2 -- JVM
bipush 3
iadd
the sum of 2 and 3 -- English
Remember: terminals don't matter.
One could give a separate abstract syntax rule
fun plus : Exp -> Exp -> Exp
and functions computing the concrete syntax as linearization:
lin plus x y = x ++ "+" ++ y -- infix
lin plus x y = "(" ++ "+" ++ x ++ y ++ ")" -- prefix
lin plus x y = "(" ++ x ++ y ++ "+" ++ ")" -- postfix
lin plus x y = x ++ y ++ "iadd" -- JVM
lin plus x y = "the sum of" ++ x ++ "and" ++ y -- English
This leads to more expressive grammars, definable in GF (Grammatical Framework).
Concrete syntaxes can be different languages.
GF has tools for visualizing trees and word alignment:
tournesol.cs.chalmers.se:41296
The fridge magnet interface:
tournesol.cs.chalmers.se:41296/fridge
To compile:
+ bipush 2
2 + 3 -------> / \ -----------> bipush 3
parse 2 3 linearize iadd
This is the idea of syntax-directed translation.
Notice: from a grammar, both parsing and linearization are created automatically.
Abstract syntax can be expressed as algebraic datatypes.
They have a direct support in Haskell, as data types.
You just have to follow the syntax convetions: constructor begin with capital letters.
data Exp = Eplus Exp Exp
| E2
| E3
This is one reason why Haskell is so well suited for compiler construction.
But: we will show later how algebraic datatypes are encoded in Java.
Concrete syntax is described by context-free grammars.
Context-free grammar = BNF grammar (Backus-Naur form).
The mathematical definition is simple:
A context-free grammar is a quadruple (T,N,S,R) where
Example (the one above):
We will follow the notation of BNF Converter (= BNFC), where
C ::= ... ;
"+"
Exp
EPlus.
From a BNF grammar, the program automatically generates
Today, we will look at how BNF grammars are written, independently of BNFC.
In a sense, the mathematical definition of BNF is its abstract syntax!
Concrete syntaxes vary: for instance, in linguistics, the common form is
Exp -> Exp + Exp
In Ansi C specification (Kernighan and Ritchie),
Exp: Exp + Exp
It is also common to group the rules with common LHS:
Exp ::= Exp "+" Exp | "2" | "3"
This is often called extended BNF (which also has other abbreviations).
This is a subset of the full definition
Gr. Grammar ::= ListRule ;
Rul. Rule ::= Ident "." Ident "::=" ListItem ;
ITerm. Item ::= String ;
INonterm. Item ::= Ident ;
NilRule. ListRule ::= ;
ConsRule. ListRule ::= Rule ";" ListRule ;
NilItem. ListItem ::= ;
ConsItem. ListItem ::= Item ListItem ;
The grammar uses two primitive (i.e. internally defined) nonterminals:
String: quoted string
Ident : letter optionally followed by letters, digits, and _ '
Graphically:
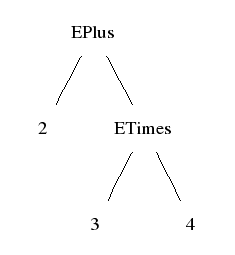 |
Haskell notation: label followed by subtrees, in parentheses if necessary:
EPlus 2 (ETimes 3 4)
Lisp notation: the same, but always in parentheses:
(EPlus 2 (ETimes 3 4))
(The original plan was to give Lisp a separate concrete syntax later!)
Usually it is good to proceed top-down: start from the largest program structures and proceed to the smallest.
In many languages, the levels are roughly:
Functional languages skip the statement level.
Each file contains a module, which is a sequence of function definitions.
A definition has a header and a sequence of statemens.
Statements are built from other statements and expressions.
Expressions are built from other expressions and atoms.
int plus (int x, int y) // definition
{
return x + y ; // statement
}
int test() // definition
{
int x ; // statements
x = readInt() ;
int y ;
y = readInt() ;
return plus(x,y) ;
}
A module is a list of definitions
Mod. Module ::= ListDef ;
NilDef. ListDef ::= ; -- empty list
ConsDef. ListDef ::= Def ListDef ; -- add one more
A function definition has a header and a list of statements in curly brackets
Fun. Def ::= Header "{" ListStm "}" ;
NilStm. ListStm ::= ;
ConsStm. ListStm ::= Stm ";" ListStm ;
A header has a type, a name (an identifier), and a parameter declaration list
Head. Header ::= Type Ident "(" ListDecl ")" ;
Sequences of different kinds are very common.
BNFC has a special notation for list categories: [C].
There is also a special notation for list rule ("Nil" and "Cons"):
terminator Stm ";" ;
abbreviates the two rules
NilStm. ListStm ::= ;
ConsStm. ListStm ::= Stm ";" ListStm ;
It says: "statements in a statement list are terminated by a semicolon".
There is also the form
separator Decl "," ;
which says: "declarations in a declaration list are separated by a comma".
A module is a list of definitions
Mod. Module ::= [Def] ;
terminator Def "" ;
Fun. Def ::= Header "{" [Stm] "}" ;
terminator Stm ";" ;
Head. Header ::= Type Ident "(" [Decl] ")" ;
A declaration has a type and an identifier:
DTyp. Decl ::= Type Ident ;
A statement is a declaration, an expression, or a return of an expression:
SDecl. Stm ::= Decl ;
SExp. Stm ::= Exp ;
SRet. Stm ::= "return" Exp ;
An expression is an identifier, a function call, an assignment, or a sum:
EId. Exp ::= Ident ;
ECall. Exp ::= Ident "(" [Exp] ")" ;
EAss. Exp ::= Ident "=" Exp ;
EPlus. Exp ::= Exp "+" Exp ;
Expressions in a list are separated by commas:
separator Exp "," ;
There is a type of integers:
TInt. Type ::= "int" ;
The category Ident is defined internally in BNFC, and needs hence
no rule. (Actually, rules for internally defined categories are illegal.)
More on atoms in next week's lectures:
Mod [
Fun
(Head
TInt
(Ident "plus")
[DTyp TInt (Ident "x"), DTyp TInt (Ident "y")])
[SRet (EPlus (EId (Ident "x")) (EId (Ident "y")))],
Fun
(Head
TInt
(Ident "test")
[])
[SDecl (DTyp TInt (Ident "x")),
SExp (EAss (Ident "x") (ECall (Ident "readInt") [])),
SDecl (DTyp TInt (Ident "y")),
SExp (EAss (Ident "y") (ECall (Ident "readInt") [])),
SRet (ECall (Ident "plus") [EId (Ident "x"),EId (Ident "y")])]]
Each category is a datatype. Lists are represented as Haskell lists.
data Module =
Mod [Def]
data Def =
Fun Header [Stm]
data Header =
Head Type Ident [Decl]
data Stm =
SDecl Decl
| SExp Exp
| SRet Exp
Ident is also a datatype.
newtype Ident = Ident String
Syntax-directed translation is implemented as pattern matching (later lecture).
Each category is an abstract class.
public abstract class Stm
public abstract class Exp
Each syntax constructor is a subclass of its value type class.
public class SDecl extends Stm {
public final Decl decl_;
}
public class SExp extends Stm {
public final Exp exp_;
}
public class EPlus extends Exp {
public final Exp exp_1, exp_2;
}
Lists are treated using Java's linked lists.
public class ListDef extends java.util.LinkedList<Def> {
}
The classes have more methods: constructors, equality, visitors.
Syntax-directed translation is implemented with visitors (later lecture).
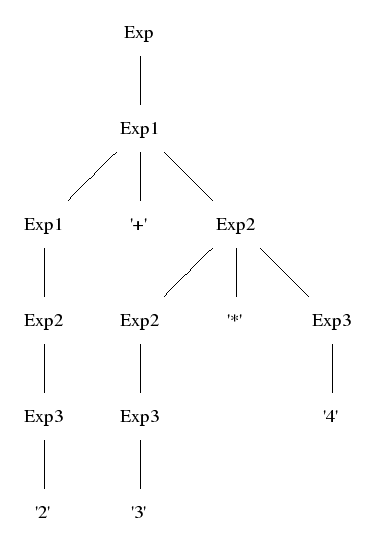
What is the syntax tree for this string?
2 + 3 + 4
Two possibilities are permitted by the grammar:
+ +
/ \ / \
+ 4 2 +
/ \ / \
2 3 3 4
Now, the arithmetic value is the same for both, so one might think it doesn't matter. But just add minus to the grammar, and consider
4 - 3 - 2
The above grammar is ambiguous: it gives more than one parse result for some strings.
Sometimes the ambiguity does not affect the meaning, sometimes it does.
Programming languages in general avoid ambiguity.
One way to avoid ambiguity in a language is to use parentheses:
Exp ::= "(" Exp "-" Exp ")"
Then the programmer is forced to write either of
(4 - (3 -2)) ((4 - 3) - 2)
However, it is much convenient to have conventions on parsing (and evaluation order):
4 - 3 - 2 == (4 - 3) - 2
4 + 3 * 2 == 4 + (3 * 2)
Parentheses always have priority over precedence and associativity:
(4 + 3) * 2 != 4 + 3 * 2
Having precedence and associativity rules in addition to grammar can be messy.
But they can simply be encoded in a BNF grammar by using precedence levels:
numeral subscripts to categories. Convention: Exp = Exp0.
EInt. Exp3 ::= Integer
ETimes. Exp2 ::= Exp2 "*" Exp3
EPlus. Exp1 ::= Exp1 "+" Exp2
The following rules implement coercions between precedence levels.
_. Exp3 ::= "(" Exp ")"
_. Exp2 ::= Exp3
_. Exp1 ::= Exp2
_. Exp ::= Exp1
Coercions are semantic dummies: they add nothing to the abstract
syntax tree. The symbol _ on the constructor place is used to indicate this.
A shorthand for such coercions groups is available:
coercions Exp 3 ;
By definition, parse trees show coercions but abstract trees don't.
  |
Mod. Module ::= [Def] ;
Fun. Def ::= Header "{" [Stm] "}" ;
terminator Def "" ;
Head. Header ::= Type Ident "(" [Decl] ")" ;
SDecl. Stm ::= Decl ;
SExp. Stm ::= Exp ;
SRet. Stm ::= "return" Exp ;
terminator Stm ";" ;
DTyp. Decl ::= Type Ident ;
separator Decl "," ;
EId. Exp2 ::= Ident ;
ECall. Exp1 ::= Ident "(" [Exp] ")" ;
EAss. Exp1 ::= Ident "=" Exp1 ;
EPlus. Exp ::= Exp "+" Exp1 ;
coercions Exp 2 ;
separator Exp "," ;
TInt. Type ::= "int" ;
Install BNFC: see
http://digitalgrammars.com/bnfc/
Generate parser and other files from the grammar
bnfc -m Imp.cf
Compile a test program
make
Run the test program on file koe.imp
./TestImp koe.imp
You can proceed by modifying Imp.cf
We will make a quick tour of Lab 1 PM
Have a tight modify-compile-test loop!
More practical details in next Tuesday's lecture.