In Chapter 27, we have seen how graphical objects can be
drawn and manipulated using the type Drawing and the
fudgets graphicsF and hyperGraphicsF. In this
chapter, we will present a set of combinators that can be used
for building syntax-oriented editors. Such editors present a
graphical view of a structured value in an abstract syntax, for
example a program in a programming language. The editors let the
user manipulate the (graphical view of) the program in various
controlled ways.
One problem the programmer must deal with, when developing
syntax-oriented editors, is how the values of the abstract syntax
should be represented, and how they should be connected to the
graphical objects. We will present a solution where the
operations on the abstract syntax is defined closely with the
corresponding operations on the graphical objects, to avoid
inconsistencies between the abstract syntax and its graphical
view.
As a concrete example, consider a grammar for a tiny expression
language with arithmetic operations on numbers.
| Expr | ::= | Integer
|
| | | Expr Op Expr
|
| Op | ::= | +
|
| | | -
|
| | | ×
|
| | | / |
Such an abstract syntax is straightforward to represent in
Haskell using one datatype for each non-terminal in the grammar,
and where each alternative corresponds to a data constructor.data Expr = Number Integer
| Operation Expr Op Expr
data Op = Add
| Subtract
| Multiply
| Divide
How should we connect these datatypes to the graphical objects?
One solution is to define Graphic instances for each type,
which means that they can be used as leaves in the type Drawing (confer Section 27.4). The drawing can be decorated
with labels containing functions for building the abstract syntax
when needed, and manipulation functions describing how the user
can modify different parts of the abstract syntax. However, all
labels in a Drawing must have the same type, which
presents a complication when we want to use different datatypes
for different non-terminals. In contrast, the combinators in this
chapter allow editors of different type, representing different
non-terminals, to be combined.
The inspiration of the combinators comes from a certain style of
parsing combinators that is part of the functional folklore (the
earliest publication we know of is [Röj95a]). If P a is the type of parsers which returns a value of type
a, the combinators that are interesting in this context
are
ap :: P (a -> b) -> P a -> P b, which combines two parsers
sequentially. It also acts as lifted function application, in
that the function returned by the first parser is applied to
the value returned by the second, yielding a value that the
combination returns.map :: (a -> b) -> P a -> P b, which applies a function to
the value that a parser returns.
The ap combinator is left associative (just like function
application), and map has higher precedence than ap. This allow a concise style when writing parsers. For
example, if pExpr is an expression parser, and pOp
is an operation parser,
Operation `map` pExpr `ap` pOp `ap` pExpr :: P Expr
parses an expression followed by an operation and another
expression, and returns the appropriate Expr value
using the Operation constructor.
The next section presents the basic combinators for
building editors. Section 28.2 shows how the combinators
can be used to build an editor for arithmetic
expressions. Section 28.3 discusses how
non-local editing operations, like variable renaming, can be
handled. The implementation of the combinators is outlined in
Section 28.4.
The combinators operate on the abstract type
SOM i
o h a (
Syntax Oriented Manipulation),
which represents a value (or piece of abstract syntax)
of type
a, that can be manipulated through input/output of
values of type
i and
o. The parameter
h is
used to pass
inherited attributes. The parameter
a
can also be used for passing synthesised attributes, if needed.
A SOM expression not only represents a (structured) value,
but also contains information about how different parts of this
value might be manipulated, and how the value should be
graphically displayed.
somF :: h -> SOM i o h a -> F (Either i (SOM i o h a))
(Either o a)
leaf :: Graphic g => g -> a -> SOM i o h a
ap :: SOM i o h (a -> b) -> SOM i o h a -> SOM i o h b
map :: (a -> b) -> SOM i o h a -> SOM i o h b
select :: (h -> a -> o)
-> (h -> a -> i -> Maybe (SOM i o h a))
-> SOM i o h a
-> SOM i o h a
attr :: (h -> a -> (h',a')) -> SOM i o h' a
-> SOM i o h a'
|
Figure 72. The SOM combinators.
The combinators that operate on SOM expressions are
shown in Figure 72. The display and manipulation
of SOM expressions are controlled by somF. The
fudget somF h s will initially display the
SOM expression s, given an attribute h to
inherit. This expression can at any time be replaced by sending
a new SOM expression to the fudget. The fudget can also
output the value that the manipulated expression
represents. This happens when a new expression is sent to the
fudget, or when a selected part of it is replaced. The message
types i and o in somF are used for the
manipulation of selected subexpressions.
Primitive SOM expressions are built with the function
leaf. The arguments to leaf are a graphical object
to display, and the value it represents. This combinator is used,
together with ap and map, to compose SOM
expressions in the same style as parsers.
To manipulate a SOM expression, the user must first
select a subexpression. A SOM expression might contain
some nodes that are not possible to manipulate (for example,
syntactic decorations like keywords), and some that are. The
programmer declares that it should be possible to select and
manipulate a node by using the select combinator. The
composition select fo fi s makes the SOM expression s selectable. When the user clicks inside the graphical
representation of s, but not inside any inner selectable
node, the composition is selected and highlighted. As a result,
the output function fo is applied to the inherited
attribute and the current value. The result is output from
the fudget somF that contains the composition, and is
typically a set of editing operations that are applicable to
the selected node. Initially, the current value is merely the
value that s represents, but this might change if some
part of s is replaced. If some input (typically an
editing operation picked by the user) is sent to the fudget
while s is selected, the input function fi
is applied to the inherited attribute, the current value and
the input, yielding a new expression which replaces select fo fi s. The input
function also has a choice of returning Nothing, in case
the input could not be handled. This is used to delegate input
to selectable ancestors, and is covered in
Section 28.3.
The combinator attr allows the inherited attribute and
the current value to be modified simultaneously. In the
composition f `attr` s, f is
applied to the inherited attribute and the current value that
s represents. The result of f is the attribute
that s will inherit, and the current value of the
composition.
By using
leaf,
ap and
map, we can turn
structured values into
SOM expressions. As an example, let
us consider the expression language from the introduction. We
will define the functions
edExpr and
edOp that
turn arithmetic expressions and operators into SOM
expressions. Since we do not need any inherited attributes for the
moment, and the type of input and output will always be the same,
we define a type synonym for the kind of SOM expressions that we
will form.
type ArithSOM a = SOM Choice [Choice] () a
edExpr :: Expr -> ArithSOM Expr
edOp :: Op -> ArithSOM Op
The expression editor
edExpr is used in
exprF
to form the fudget that presents the editor.
exprF :: Expr -> F (Either Choice (ArithSOM Expr))
(Either [Choice] Expr)
exprF e = somF () (edExpr e)
When the user selects a subexpression,
exprF outputs a
list of choices that is presented in a menu. These choices
represent the operations that are available on the
subexpression. If a choice is picked, it will be sent back to
the editor.
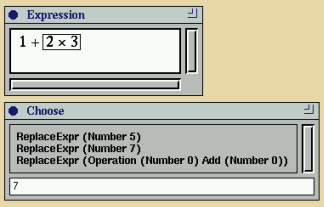
exprF also outputs the arithmetic
expression for evaluation in the main fudget. A screen dump
of the program is shown in
Figure 73.
Figure 73. An arithmetic expression manipulator. The
user has selected the subexpression 2 × 3, which can
be replaced by 5, 7, or 0 + 0.
main = fudlogue $
loopF (shellF "Choose" (smallPickListF show >+<
(displayF >=^< (show . evalExpr))) >==<
shellF "Expression" (scrollF (exprF (Number 0)))
)
evalExpr :: Expr -> Integer
evalExpr (Number i) = i
evalExpr (Operation e1 b e2) = evalOp b (evalExpr e1)
(evalExpr e2)
evalOp :: Op -> (Integer -> Integer -> Integer)
evalOp Add = (+)
evalOp Subtract = (-)
evalOp Multiply = (*)
evalOp Divide = \x y -> if y == 0 then 0 else x `div` y
When we define
edExpr and
edOp, we use a
programming style which resembles the one we presented for
parsing combinators in the introduction:
edExpr e = selExpr $ case e of
Number i -> Number `map`
leaf i i
Operation e1 b e2 -> Operation `map`
edExpr e1 `ap`
edOp b `ap`
edExpr e2
Numbers are shown as they are, whereas binary expressions
are handled recursively and by means of
edOp. Each
subexpression can be selected and manipulated by
selExpr, which is defined later.
The definition of edOp is similar.
edOp b = selOp $ leaf (showOp b) b
showOp Add = "+"
showOp Subtract = "-"
showOp Multiply = "×"
showOp Divide = "/"
We define the type
Choice to contain expressions that
can replace the selected subexpression. Since subexpressions
can be of both type
Expr and
Op, we use a union
type for the output.
data Choice = ReplaceExpr Expr
| ReplaceOp Op
When the user selects an expression, we arbitrarily choose
to present three alternatives which let the user replace the
expression with its value plus or minus one, or replace it
with
0 + 0. The interface is not at all the most
convenient one could imagine, but it allows a patient user to
enter an arbitrary expression (the
+ can be replaced
with any of the other operators, as we will see below). This
part of the editor could of course be elaborated as desired.
selExpr :: ArithSOM Expr -> ArithSOM Expr
selExpr = select outf inf
where
outf _ e = map ReplaceExpr
[Number (evalExpr e-1),
Number (evalExpr e+1),
Operation (Number 0) Add (Number 0)]
inf _ _ = map edExpr . stripExpr
stripExpr (ReplaceExpr e) = Just e
stripExpr _ = Nothing
If the user picks one of the choices, it will be propagated
to the selected node, the expression is extracted from the
type union, and a replacement
SOM expression is
formed. However, the type system cannot prevent programming
errors that result in an operator being sent to
selExpr. To get a more robust program, the function
stripExpr ignores the input in this case and returns
Nothing.
When an operator is selected, we present a choice of the four
arithmetic operators.
selOp :: ArithSOM Op -> ArithSOM Op
selOp = select outf inf
where
outf _ _ = map ReplaceOp [Add,Subtract,Multiply,Divide]
inf _ _ = map edOp . stripOp
stripOp (ReplaceOp b) = Just b
stripOp _ = Nothing
With the combinators presented so far, we can define local
manipulation operations. The user can select a
SOM
subexpression, and arbitrary replacements can be specified for
that expression. If a manipulation would imply a change in
other parts of the expression, we are forced to replace the
complete expression globally, by sending a new
SOM
expression to
somF. There are situations where we want
the possibility to specify replacements that are somewhere in
between the local and global alternatives. Suppose that we want
to add variables to our arithmetic expressions. We would then
like to provide an operation for changing the name of a
variable, by selecting one occurrence (possibly the binding
occurrence), and give a new name to it. This is an operation
that affects the whole subtree that starts with the binding of
the variable.
This effect can be achieved by using the possibility to delegate input as follows. Recall that the input function (the
second parameter of select) can return Nothing
for input that cannot be handled. Instead of discarding the
input, somF will delegate it to the closest selectable
ancestor, and apply its input function. This delegation
propagates towards the root of the SOM expression, until
a select node is found that accepts the input.
In the case of variable manipulation, delegation can be used to
propagate input to the node where the variable is bound. We will
do this in the following section, where we present a variant of
the expression manipulator in Section 28.2, extended
with variables.
We extend the datatype
Expr with constructors for
variables and let expressions.
data Expr =
...
| Var Name
| Let Name Expr Expr
type Name = String
In the construction of a
SOM expression, we assume
the presence of an environment where we can lookup the
value of variables.
type Env = [(Name,Integer)]
We will use the inherited attribute for propagating the
environment. The type of SOM expressions we will use are
instances of
ArithEnvSOM.
type ArithEnvSOM a = SOM Choice [Choice] Env a
We introduce the additional combinators
drLeft or
drRight to prepend or append a graphical decoration to
an expression.
drLeft :: Graphic g => g -> SOM i o h a -> SOM i o h a
drRight :: Graphic g => SOM i o h a -> g -> SOM i o h a
These are used for drawing keywords, as we will see in the
case of let expressions.
The associativity of ap, drLeft and drRight are set so that we avoid parentheses, at least in
this application.
infixl 3 `ap`
infixr 8 `drLeft`
infixl 8 `drRight`
Haskell does not declare any fixity for
map, which
means that it gets a default declaration.
infixl 9 `map`
But the type of
map suggests that it should be
right associative. If it were, and had the same precedence
level as
drLeft, we could skip the parentheses in
expressions like
f `map` (d `drLeft`
s). If local fixity declarations were allowed in
Haskell, we could fix the fixity.
edExpr e =
let infixr 8 `map`
in ...
Local fixity declarations are not allowed in Haskell, so we
give
map a new name with the desired fixity.
infixr 8 `mapp`
mapp :: (a -> b) -> SOM i o h a -> SOM i o h b
mapp = map
With
mapp, we can construct
SOM expressions in
the style shown in in
Figure 74.
edExpr :: Expr -> ArithEnvSOM Expr
edExpr e = case e of
Number i -> selExpr $ Number `mapp`
leaf i i
Operation e1 b e2 -> selExpr $ Operation `mapp`
edExpr e1 `ap`
edOp b `ap`
edExpr e2
Var n -> selVar n $ Var `mapp`
leaf n n
Let n e1 e2 -> selLet $ extendEnv `attr`
Let `mapp`
"let" `drLeft`
edName n `ap`
"=" `drLeft`
(dropEnv `attr` edExpr e1) `ap`
"in" `drLeft`
edExpr e2
extendEnv :: Env -> Expr -> (Env,Expr)
extendEnv = \env e@(Let n e1 _) -> ((n,evalExpr env e1):env,e)
dropEnv :: Env -> Expr -> (Env,Expr)
dropEnv = \env e -> (tail env,e)
|
Figure 74. The function edExpr
extended for variables.
The function extendEnv will be applied to the
current let expression, from which it will extract
sufficient information to extend the environment that the
body should inherit. To avoid that the right-hand side in
the let expression also inherits the extended environment,
we use the function dropEnv to pop the added
binding. (If we want to allow recursive declarations, we
omit dropEnv.)
Note that we have also used different selection functions for
different kinds of expressions. Variables are handled by
selVar, let expressions by selLet, and the
others by selExpr.
The binding occurrence of a variable is handled by edName (Figure 75), and selecting such a name
results in a choice of renaming it. For simplicity, we pick
an arbitrary new name that is not present in the
environment by using freshVar.
edName :: Name -> ArithEnvSOM Name
edName n = selName $ leaf n n
selName :: ArithEnvSOM Name -> ArithEnvSOM Name
selName = select outf inf
where outf env n = [renameCommand n env]
inf _ _ _ = Nothing
renameCommand :: Name -> Env -> Choice
renameCommand old env = Rename old (freshVar env)
freshVar :: Env -> Name
freshVar env = head (map (:[]) ['a'..] \\ map fst env)
|
Figure 75. The editor for variable names.
The input function in selName ignores all input,
which instead is delegated to selLet.
We have extended the manipulation type with a command for
renaming a variable.
data Choice =
...
| Rename Name Name
The selection functions are defined in
Figure 76.
selExpr :: ArithEnvSOM Expr -> ArithEnvSOM Expr
selExpr = selExpr' (const []) exprInf
selLet :: ArithEnvSOM Expr -> ArithEnvSOM Expr
selLet = selExpr' (const []) letinf
where letinf env (Let n e1 e2) (Rename n' new) | n == n'
= Just (edExpr (Let new (rename n new e1)
(rename n new e2)))
letinf env e i = exprInf env e i
selVar :: Name -> ArithEnvSOM Expr -> ArithEnvSOM Expr
selVar n = selExpr' (\env -> [renameCommand n env]) exprInf
selExpr' :: (Env -> [Choice])
-> (Env -> Expr -> Choice
-> Maybe (ArithEnvSOM Expr))
-> ArithEnvSOM Expr
-> ArithEnvSOM Expr
selExpr' xchoices inf = select outf inf
where outf env e = xchoices env ++
map ReplaceExpr
([ Number (v+1)
, Number (v-1)
, Operation n0 Add n0
, Let (freshVar env) n0 n0 ]
++ map (Var . fst) env
)
where v = evalExpr env e
n0 = Number 0
exprInf :: Env -> Expr -> Choice -> Maybe (ArithEnvSOM Expr)
exprInf env _ = map edExpr . stripExpr
|
Figure 76. The selection functions for expressions.
The functions for let expressions and variables
are variants of the original selExpr from
Section 28.2. We define a parameterised version ( selExpr'), which lets us add choices and specify the input
function. Note that we have added choices for all variables
in scope.
The standard selection function (selExpr) does not
have any additional choices, whereas the selection function
for let expressions (selLet) defines an extended
input function which handles the renaming command. For a
renaming command to match, the old variable must equal the
bound variable. Otherwise, input is meant for some outer
let expression. We assume a function rename, where
rename old new e substitutes
new for old in e.
When selecting a variable, we extend the expression
selection menu with a renaming choice. Variable renaming
can then take place at any occurrence of a variable. Note
that we do not handle renaming in the input function, it is
the same as in selExpr.
The rest of the program is almost the same as in the first
example, except that we pass the empty environment as an
initial inherited attribute in exprF. The program is
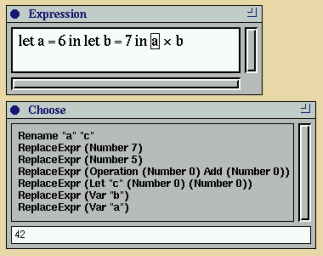
seen in action in Figure 77.
exprF :: Expr -> F (Either Choice (ArithEnvSOM Expr))
(Either [Choice] Expr)
exprF e = somF emptyEnv (edExpr e)
emptyEnv :: Env
emptyEnv = []
Figure 77. Manipulating variables. There are
additional choices for the variables in the
environment. Since a variable is selected, there is also a
choice of renaming it.
We have taken the approach to implement
SOM as a
datatype with constructors corresponding to the combinators
leaf,
select,
map and
ap. Since
the types of the arguments to
map and
ap have
variables that do not show up in the result type, we use the
possibility to specify local existential quantification using
variables beginning with
? in the datatype
declaration. Again, existential quantification in datatypes
proves to be a useful extension to Haskell (see also
Section 27.4.2).
data SOM i o h a =
Select (h -> a -> o)
(h -> a -> i -> Maybe (SOM i o h a))
(SOM i o h a)
| Map (?b -> a) (SOM i o h ?b)
| Ap (SOM i o h (?b -> a)) (SOM i o h ?b)
| Attr (h -> ?a -> (?h,a)) (SOM i o ?h ?a)
| Leaf Dr a
| Decor (Dr -> Dr) (SOM i o h a)
The first four constructors correspond directly to the
respective combinators.
select = Select
ap = Ap
attr = Attr
instance Functor (SOM i o h) where map = Map
The first argument to the
Leaf constructor is a
drawing:
type Dr = Drawing SOMPointer Gfx
The label type
SOMPointer, which is defined later, is
used to identify what part of a
SOM expression the
user has selected. The type
Gfx is used to store
arbitrary graphical objects in the leaves (
Section 27.4.2). In the definition of
leaf,
we turn these graphics into drawings by means of
g
(which was defined in
Section 27.4.2).
leaf :: Graphic g => g -> a -> SOM i o h a
leaf d a = Leaf (g d) a
The final constructor in
SOM is
Decor, and can
be used to define layout or add additional graphics on a part
of a
SOM expression. Its first argument is a function
which will be applied to a drawing that is constructed from its
second argument. The combinators
drLeft and
drRight uses this constructor:
drLeft d n = Decor (\d' -> hboxD [g d,d']) n
drRight n d = Decor (\d' -> hboxD [d',g d]) n
The fudget
somF is built around a
hyperGraphicsF, which outputs a
SelectionPtr whenever
the user selects a subexpression.
data Dir = Le | Ri
type SelectionPtr = [Dir]
A
SelectionPtr is a list of turns to take whenever an
Ap node is encountered in the
SOM tree, and
points out a
select node. Using the function
somOutput in
Figure 78,
somF can get the
output choices of a selected node.
somOutput :: h -> SOM i o h a -> SelectionPtr -> o
somOutput h n p = case n of
Select outf _ n -> case p of
[] -> outf h (somValue h n)
_ -> somOutput h n p
Ap f n -> case p of
Le:p -> somOutput h f p
Ri:p -> somOutput h n p
Map _ n -> somOutput h n p
Attr f n -> somOutput (fst (apAttr f h n)) n p
Decor _ n -> somOutput h n p
|
Figure 78. The function somOutput.
If somF receives an input choice for the selected
node, the function somInput (Figure 79) is
applied to the input and the selection pointer, to
get the modified SOM tree.
somInput :: h -> SOM i o h a -> i -> SelectionPtr
-> Maybe (SelectionPtr,SOM i o h a)
somInput h n i p = case n of
Select o inf n -> case p of
[] -> myInput
_ -> mapSOM (Select o inf)
(somInput h n i p)
++ myInput
where myInput = map (\n->([],n))
(inf h (somValue h n) i)
Ap f n -> case p of
[] -> Nothing
Le:p -> map (mapPair ((Le:),(`ap` n)))
(somInput h f i p)
Ri:p -> map (mapPair ((Ri:),(f `ap`)))
(somInput h n i p)
Map f n -> mapSOM (Map f)
(somInput h n i p)
Attr f n -> mapSOM (Attr f)
(somInput (fst (apAttr f h n)) n i p)
Leaf dr a -> Nothing
Decor f n -> mapSOM (Decor f)
(somInput h n i p)
where mapSOM = map . apSnd
mapPair f g (x,y) = (f x,g y)
|
Figure 79. The function somInput.
somInput also returns the pointer to the node whose
input function accepted the input, which is used by somF to update the correct part of the drawing. If all input
functions ignore the input, somInput returns Nothing.
The functions somOutput and somInput use the
function somValue, to get the current value of a SOM expression, and the function apAttr, to apply
attribute functions (Figure 80).
somValue :: h -> SOM i o h a -> a
somValue h n = case n of
Select _ _ n -> somValue h n
Ap n1 n2 -> (somValue h n1) (somValue h n2)
Map f n -> f (somValue h n)
Leaf _ a -> a
Attr f n -> snd (apAttr f h n)
Decor _ n -> somValue h n
apAttr :: (h -> a -> (h',a'))
-> h
-> SOM i o h' a
-> (h',a')
apAttr f h n = h'a' where h'a' = f h (somValue (fst h'a') n)
|
Figure 80. The functions somValue and
apAttr.
The recursive definition in apAttr mirrors the fact
that attributes and values can have cyclic dependencies.
The implementation of somF is shown in Figure 81,
and as mentioned previously, it is built around hyperGraphicsF. The auxiliary functions tohg, out, updateDr, and replaceDr are routing
functions that are typical when programming with loopThroughRightF. The function out is used when
outputting messages from somF, and updateDr and
replaceDr are used when updating part of or the whole
of the drawing in the hyperGraphicsF. (Compare with
the type of hyperGraphicsF in Section 27.4.)
The controlling stream processor ctrl has an internal
state which consists of the SOM expression being
edited (n), and a pointer to the selected node ( p). If there is no selected node, p is Nothing. An incoming message to ctrl is either a
click from the hyperGraphicsF, indicating a new
selection by the user (handled by click), an input
choice (handled by input) or a new SOM
expression (handled by replace).
In click, the
old selection cursor is removed, and a new node is
selected.
In input, it is checked that there is a
selection, and that a replacement node can be obtained from
somInput. In this case, the appropriate subdrawing is
replaced, and selected.
somF :: h -> SOM i o h a -> F (Either i (SOM i o h a))
(Either o a)
somF h n = loopThroughRightF
(absF (ctrl n Nothing))
(hyperGraphicsF (unselectedSomDr n))
where
tohg = putSP . Left
out = putSP . Right
updateDr = tohg . Left . unselectedSomDr
replaceDr = tohg . Right
unselectedSomDr = somDrawing []
ctrl n p = getSP $ click `either` (input `either` replace)
where
same = ctrl n p
click p' = maybe id (deselect n) p $
selectO n p' $
ctrl n (Just p')
input i = flip (maybe same) p $ \jp ->
flip (maybe same) (somInput h n i jp) $ \(rp,n') ->
replaceDr (rp,somDrawing rp n') $
selectO n' jp $
out (Right (somValue h n')) $
ctrl n' p
replace n' = updateDr n' $
ctrl n' Nothing
-- Select subnode and send its output.
selectO n p = select n p . out (Left (somOutput h n p))
-- Draw cursor
select = setselect cursor
-- Remove cursor
deselect = setselect id
setselect cu n p = replaceDr (p,cu (somDrawing p n))
-- The cursor is a frame around the node
cursor d = placedD overlayP (boxD [d,(g (frame' 1))])
-- Extract selected subdrawing
somDrawing :: SelectionPtr -> SOM i o h a -> Dr |
Figure 81. The function somF.