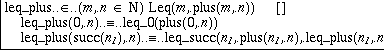relation
and prove two results: that
relation
and prove two results: that
 is transitive and that
is transitive and that 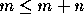 for all natural numbers m and n.
for all natural numbers m and n.




In this section we give a detailed presentation of how the system is used
to develop a small example. We define the set of natural numbers, define
addition and the  relation
and prove two results: that
relation
and prove two results: that
 is transitive and that
is transitive and that 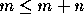 for all natural numbers m and n.
for all natural numbers m and n.
When ALF is started two windows appear on screen: the theory window and the scratch window. Both are split into subwindows by horizontal lines; the theory window consists of two subwindows and the scratch window of three. All five subwindows are initially empty. In the initial state only the basic type theory is known to the system. A theory is developed by making a sequence of definitions of various kinds. At the top of the scratch window we find a menu bar. We use the mouse to select (with any mouse button) the Define entry and the following menu appears:
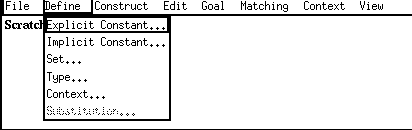
The different entries represent the kinds of objects that can be defined. We will introduce them one at a time and start to define the set of natural numbers. So we move the mouse cursor to the entry Set... and release the mouse button. A small text editor window pops up and prompts us to give the name of the set to be defined. We type the name N:
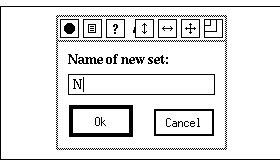
We then strike the Return key (or click on the Ok button) and the pop-up window disappears. Instead the incomplete definition appears in the scratch area, which is the top subwindow of the scratch window:
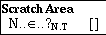
The first reason that the definition is incomplete is that the type of the
new constant N has not yet been specified, as can be seen from its type
 . For the moment we ignore the significance of the subscript. It
suffices to know that we have to complete the definition of this
placeholder.
We also ignore the empty pair of brackets following the definition.
So we select the placeholder, using the left mouse button. It appears
in inverted video
and we click on the right mouse button to get a menu with the available
options:
. For the moment we ignore the significance of the subscript. It
suffices to know that we have to complete the definition of this
placeholder.
We also ignore the empty pair of brackets following the definition.
So we select the placeholder, using the left mouse button. It appears
in inverted video
and we click on the right mouse button to get a menu with the available
options:
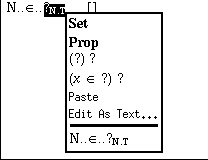
The choices Set and Prop represent the two predefined ground types
of sets and propositions, respectively. (These two are actually synonyms,
because of the identification of proposition and sets). The two next choices
represent non-dependent and dependent function types. There is also the
possibility to paste a type from some previous definition or to invoke the
text editor. These six items are always present in this menu when the
selection is a type expression. At the end
there is a context-sensitive part, where additional possibilities may appear.
In our case we choose the first item, i.e. Set and the placeholder
is replaced by our choice. You may wonder at this point why we had to make
this choice since we already had indicated that we wanted to define a set.
This will be explained below, when we define  .
.
It is now clear to the system that the name N denotes a set. However, to complete the definition we have to give the constructors of the set. In this case the constructors are 0 and the successor function. To define these, we select N (left mouse button!) and invoke the menu of options (right button!):
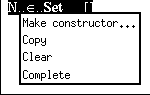
It should be obvious that the choice should be Make constructor....
The text editor window pops up and we type 0 as the name of the first
constructor. When the window closes, we see in the scratch area that we
have to give the type of 0. We select the placeholder for the type and
invoke the command menu. Now the final, context-sensitive item
N  Set is the correct choice
Set is the correct choice and the situation is the following:
and the situation is the following:

As should be apparent already now, the ALF user does almost all work by selecting items using the left mouse button and invoking the pop-up menu of commands applicable to the selection with the right button. Occasionally some text has to be typed in the pop-up text editor.
We are not yet finished with N; there is one more constructor. So we select
N, choose Make constructor... from the command menu and type
succ in the editor. The next step is to give the type of succ.
Since it is a function, we should choose a function type from the command
menu. The type of the successor function is non-dependent, so we could use
the (?)? entry. However, if we have a preferred
variable name to use for an unspecified argument to the function, it is
convenient to indicate this now. This will be explained in more detail below,
so let us for the moment accept that it is a good idea to choose the
(x  ?)? entry. The text editor prompts us for a name and we type n.
There are now two placeholders in the type for succ and we select them in
turn and use the pop up menu to set them to N. The definition of the
set of natural numbers is now complete:
?)? entry. The text editor prompts us for a name and we type n.
There are now two placeholders in the type for succ and we select them in
turn and use the pop up menu to set them to N. The definition of the
set of natural numbers is now complete:
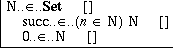
Before we continue, we consider briefly what one can do in case of mistakes.
Select the type of succ, i.e. (n 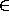 N)N. In doing this, note
that the selection is always a complete subexpression. Thus the best way
of selecting the entire type is to click on one of the parentheses, since
the smallest enclosing expression is then the entire type. Now invoke the
pop up menu and choose Clear. The type is replaced by a placeholder and we
may start again to give the type
N)N. In doing this, note
that the selection is always a complete subexpression. Thus the best way
of selecting the entire type is to click on one of the parentheses, since
the smallest enclosing expression is then the entire type. Now invoke the
pop up menu and choose Clear. The type is replaced by a placeholder and we
may start again to give the type . To do this, we use another
method: We double-click on the place-holder and the text editor pops up.
We may now give the entire type (using colon for
. To do this, we use another
method: We double-click on the place-holder and the text editor pops up.
We may now give the entire type (using colon for 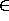 ): (n:N)N.
This is a general feature; by double-clicking when selecting, the text editor
pops up and one may edit the expression as text. Of course, this may produce
a syntactically incorrect
expression. In that case, one gets an error message and may open the
editor again to correct the error.
): (n:N)N.
This is a general feature; by double-clicking when selecting, the text editor
pops up and one may edit the expression as text. Of course, this may produce
a syntactically incorrect
expression. In that case, one gets an error message and may open the
editor again to correct the error.
The definition of N is now complete. We select it (click on N) and invoke Move-to-theory from the pop-up menu. The definition disappears from the scratch area and appears instead in the lower half of the theory window. Completed definitions should be moved to the theory. If it is necessary to change an already completed definition one has to move it back to the scratch area first by selecting it and choosing Move-to-scratch. If necessary multiple definitions have to be selected ( shift left-button) and moved at once.
As our next step, we define the constants 1 and 2 as abbreviations or, in ALF terminology, explicit constants. To do this, open the Define menu and choose Explicit constant.... When prompted for the name, we answer 1 and the result in the scratch area is

Both the type and the value of this constant have to be defined. We may start with either. We choose the type, so we select this placeholder and find the choice N in the pop-up menu. Next, we select the value placeholder and find succ in the menu. Choosing this will have the effect
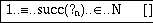
i.e., a new placeholder is inserted for the argument to succ. The
type-checker of ALF has realized that if 1 is to be a natural number,
it cannot be succ itself, but rather succ applied to a natural
number. We complete the definition by selecting the remaining placeholder and
choosing 0 from the menu. Here we can also note that in the menu we are
also offered the choice 1 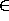 N, which would give the circular
definition 1
N, which would give the circular
definition 1  succ(1)
succ(1) 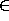 N. If this choice is attempted, an
error message results. We see from this example that the context-sensitive
choices offered are somewhat roughly computed and may not always be
possible to select. In a similar way we define 2 as succ(1).
N. If this choice is attempted, an
error message results. We see from this example that the context-sensitive
choices offered are somewhat roughly computed and may not always be
possible to select. In a similar way we define 2 as succ(1).
We go on to define addition. This can be done by a pair of recursive equations with case analysis on one of the arguments. In ALF terminology, this is an implicit constant. We note here also that the present version does not admit infix operators, so we prefer the name plus. The first step is to choose Implicit constant... from the Define menu and reply with this name when prompted. The next step is to give the type of the constant. We choose to do this with the text editor (double-click!):
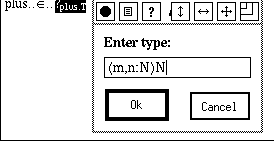
To fill in the definition, we select the name plus and choose Make pattern from the menu. A defining equation with a placeholder as right-hand side appears. However, we cannot fill in this placeholder yet. We want to do case analysis on the first argument (the choice of the first rather than the second is arbitrary), so we select the parameter m in the left-hand side and invoke Make pattern again. The equation is split in two, one for each possible constructor form of N. Now the right hand sides of the equations can be easily filled in, by a sequence of selections and choices from the pop-up menu.
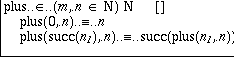
We have defined plus by pattern-matching on its first argument. In such definitions, we allow recursive calls. To ensure that a recursive definition leads to a well-defined function it is necessary that there is an argument position in which the recursive call has a structurally smaller argument. In the case of plus, the first argument has this property. The present version of ALF does not enforce this condition. It is thus possible in ALF to make meaningless recursive definitions, such as f(x) = f(x). The user must manually check that recursive definitions are well-formed.
We may now move our completed definitions to the theory and go on to define Leq, the relation ``less than or equal to'' on N. For any two natural numbers m and n, Leq(m,n) is a proposition or, equivalently, a set. The ALF action to define this is therefore to choose Set... from the Define menu and choose the name Leq when prompted by the text editor. This leaves us in the situation
and we now see why we have to give the type of Leq also in the Set... case. Leq is not a set itself; rather it is a function that given two natural numbers produces a set. We say that Leq is a family of sets. So we may double-click on the placeholder for the type and type (m,n:N)Set. We note that we have our first example of a dependent set; for each choice of m and n we have a distinct set (proposition), whose elements are the proofs of the proposition. Of course, this will mean that Leq(2,1) will have to be defined to be empty, while Leq(1,2) will be inhabited. Next we have to give the constructors. There are many ways to define Leq. A convenient one is an inductive definition: we have Leq(0,n) for any n and also that Leq(succ(m),succ(n)) if Leq(m,n). These two cases will give the constructors of the set. We have to invent two names for the two cases and define the constructors as before:
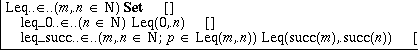
To help understand this definition, we can check that leq_0(1) is a proof (element) of Leq(0,1) and leq_succ(0,1,leq_0(1)) a proof of Leq(1,2). As a more interesting example, we now prove that Leq is transitive. This theorem is represented by the set (m,n,k:N; p:Leq(m,n); q:Leq(n,k))Leq(m,k). To prove it, we have to define a constant leq_trans of this type. Since the theorem involves arbitrary natural numbers, we define this as an implicit (recursive) constant. The first steps, including the first Make pattern, give the situation

It now seems natural, following the ideas in defining plus, to do pattern matching on one of the natural number arguments. However, it turns out to be even better to do pattern matching on the proof arguments p and q. To do this, we first have to move the definition of the family Leq to the theory, since we are not permitted to do pattern matching on an argument whose type is in the scratch area. (Such a definition could later be extended with another constructor, which would invalidate the pattern matching done). After having done this, we select p and invoke Make pattern. The following happens:
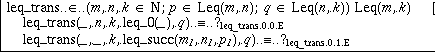
The two constructors for Leq appear in the respective cases, but some
arguments have been replaced by a wildcard _. This is
because there is a dependency between the arguments. In the first equation,
the third argument leq_0(_) has (according to the typing of
leq_trans) type Leq(m,n). On the other hand, according to the
definition of Leq, leq_0(x) has for any x type
Leq(0,x). These two types are now unified and ALF is able to
conclude that m must be 0 and that also x=n. The latter
is enforced by choosing n as argument to leq_0. Such inferred
arguments are not displayed by the system but instead shown as a wildcard.
This device maintains the patterns in linear form, i.e. no variable
appears more than once.
The first equation can now easily be completed. To do this, we select the right hand side. Here we note a fact that we have not mentioned before. The small bottom subwindow of the scratch window displays the type of the selection, in this case Leq(0,k). An element of this type is obvious: it is leq_0(k), which we construct by choosing leq_0 from the pop-up menu. The argument k is inferred by the system and filled in automatically. It remains to define the right hand side of the second equation. Selecting it we see its type Leq(succ(m1),k)) at the bottom of the theory window. We cannot directly give a proof of this; leq_succ requires both its first two arguments to be on successor form. Thus we do pattern matching on q. Now something interesting happens; only one of the cases appear:
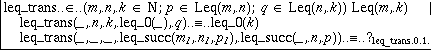
The reason for this is apparent when the situation is analyzed: Since p now has constructor leq_succ, n cannot be 0 and thus the proof q:Leq(n,k) cannot have constructor leq_0. The type of the right hand side of the remaining case is Leq(succ(m1),succ(n)) and an application of leq_succ seems appropriate. We try this and the right hand side is partly completed to leq_succ(m,n,?), where the remaining placeholder has type Leq(m1,n). The situation is the following, where we have opened the pop-up menu to see what is available to us:

We see that we have p1 and p available, which would give us a term of the required type by a recursive application of leq_trans itself. We make this choice and have to fill in the arguments p1 and p, which cannot be inferred by the system. This completes the proof and it remains only to check that the recursive call is on a structurally smaller argument. This is indeed the case, as the third argument in the recursive call is on p1, which is one of the arguments to the constructor in the corresponding position on the left hand side.
Finally, we prove the simple result leq_plus:(m,n:N)Leq(m,plus(m,n)). We define this as an implicit constant and do pattern matching on m. This gives us

Selecting the right hand side of the first equation, we find that its type is Leq(0,plus(0,n)). But according to the definition of plus, plus(0,n) is definitionally equal to n, which means that the required type is the same as Leq(0,n), for which we can easily find the proof leq_0(n). Similarly, in the second case, ALF can use the second defining equality for plus to compute the type of the right hand side to Leq(succ(m),succ(plus(m,n))) and we can complete the proof with leq_succ, using a recursive call to leq_plus as third argument: