The examples in this lecture run in GHC <= version 7.8. If you have GHC >= version 7.10, you need some extra lines — see the source code — to make it work. However, you do not need to understand them. We will cover the reason for such extra lines in the next lecture.

Monads

Some programming features in imperative languages

Error handling
- Exceptions (e.g., Java)
- Set some global variable and abort computation (e.g., errno in C)
Logging
- Writing to a file
- Having a global reference where to store the log

What about in Haskell? (Pure functional language)

Data flow is explicit!

Let us take a concrete example

 -- | Abstract syntax
 data Expr = Con Int | Div Expr Expr

 -- | Simple interpreter for simple arithmetic expressions
 interp :: Expr -> Int
 interp (Con i)     = i
 interp (Div e1 e2) = i1 `div` i2
     where i1 = interp e1
           i2 = interp e2

 -- | Succesful division
 ex_ok    = Div (Con 10) (Con 5)

What if we accidentally divide a number by 0?
```
-- | Crashing!
ex_crash = Div (Con 1) (Con 0)
```
Everything crashes!

Handling errors explicitly

The error handling mechanism that we consider is

If something goes wrong, the whole computation aborts!

(We do not consider recovery options)

Let us modify the interpreter to implement our error handling mechanism

 data E a = Value a | Wrong

 interpE :: Expr -> E Int
 interpE (Con i)     = Value i
 interpE (Div e1 e2) = case maybe_i1 of
                         Wrong -> Wrong
                         Value i1 -> case maybe_i2 of
                                     Wrong -> Wrong
                                     Value i2 -> if i2 == 0 then Wrong
                                                            else Value $ i1 `div` i2
     where maybe_i1 = interpE e1
           maybe_i2 = interpE e2

Basically, every recursive call needs to be checked for errors! If one of them fails, then the program should abort.
Consider what would happen if Expr had many other recursive constructors

One possible run function

runE :: Expr -> IO ()
runE e = case interpE e of
              Wrong -> putStrLn "Something went wrong!"
              Value i -> putStrLn $ show i

Logging

We want to create a trace of the program
- Send messages to a log
- This information could be used to improve future interpreter optimizations or detection of bugs
  We want to send messages to a log at every instruction

Let us modify the interpreter to log the number of divisions.

 data L a = L (a, [String])

 interpL :: Expr -> L Int
 interpL (Con i)      = L (i, ["-- Hit Con --\n"])
 interpL (Div e1 e2)  = L (i1 `div` i2,
                           "-- Hit a Div --\n" :
                           "** Left recursive call**\n" :
                           msgs1 ++
                           "** Right recursive call**\n" :
                           msgs2 )
    where L (i1, msgs1) = interpL e1
          L (i2, msgs2) = interpL e2

Basically, the results of every recursive call* needs to be inspected to obtain the corresponding logs.
Consider what would happen if Expr had many other recursive constructors

One possible run function

 runL :: Expr -> IO ()
 runL e = do putStr "The result is:"
             putStrLn $ show i
             putStrLn "Log:"
             putStrLn $ show msgs
    where L (i,msgs) = interpL e

Side-effects & pure functional programming

Imperative programming	Pure functional programming
Error handling	Plumbing (check if any subcomputation has failed)
Logging	Plumbing (consider subcomputations' logs)

Monads

What are monads?
- Special data structures useful to write programs
- Any program?
  Programs with side-effects!
What is so special about such data types?

It is general! (supports many different side-effects)

Monads hide the plumbing! (simplifies code)
How is so general?
Monads control the order of evaluation
Roughly speaking, the trick is how the ; is defined! Different definitions for ; allows to handle different side-effects.

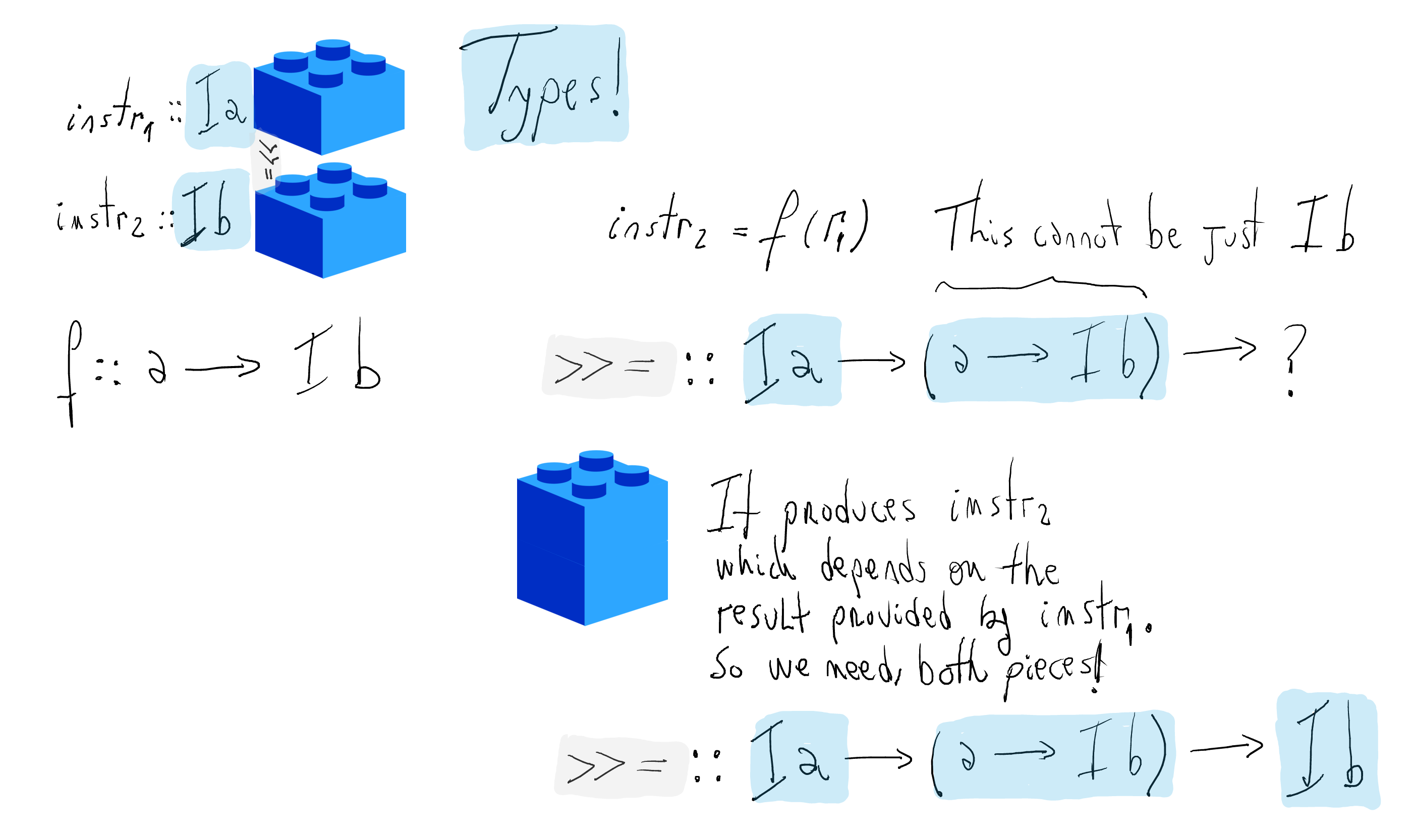
Construction of programs

Programs can be conceived as a sequence of instructions put together
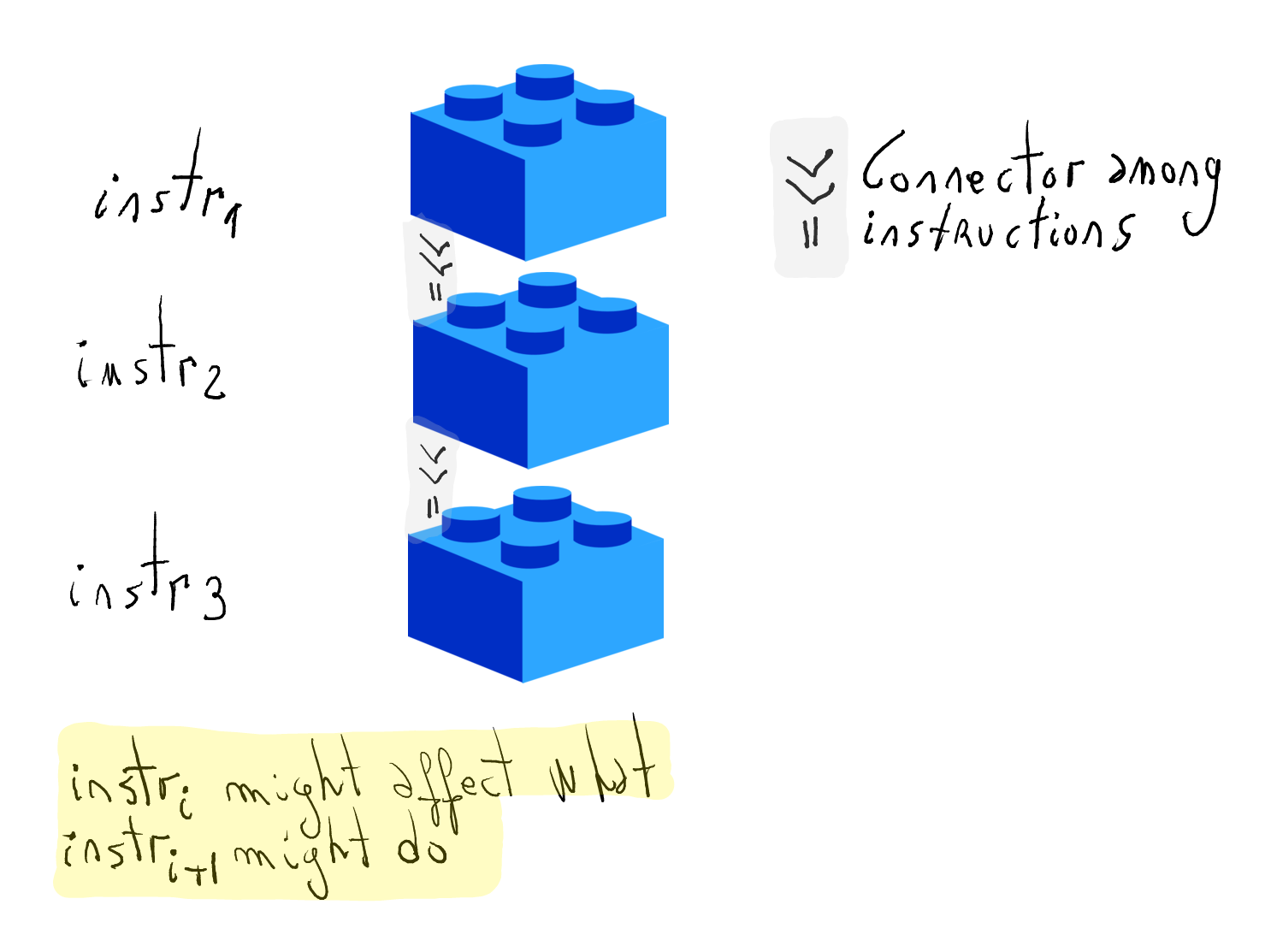
Every instruction computes some data
Importantly, an instruction can affect what subsequent ones do. More precisely,

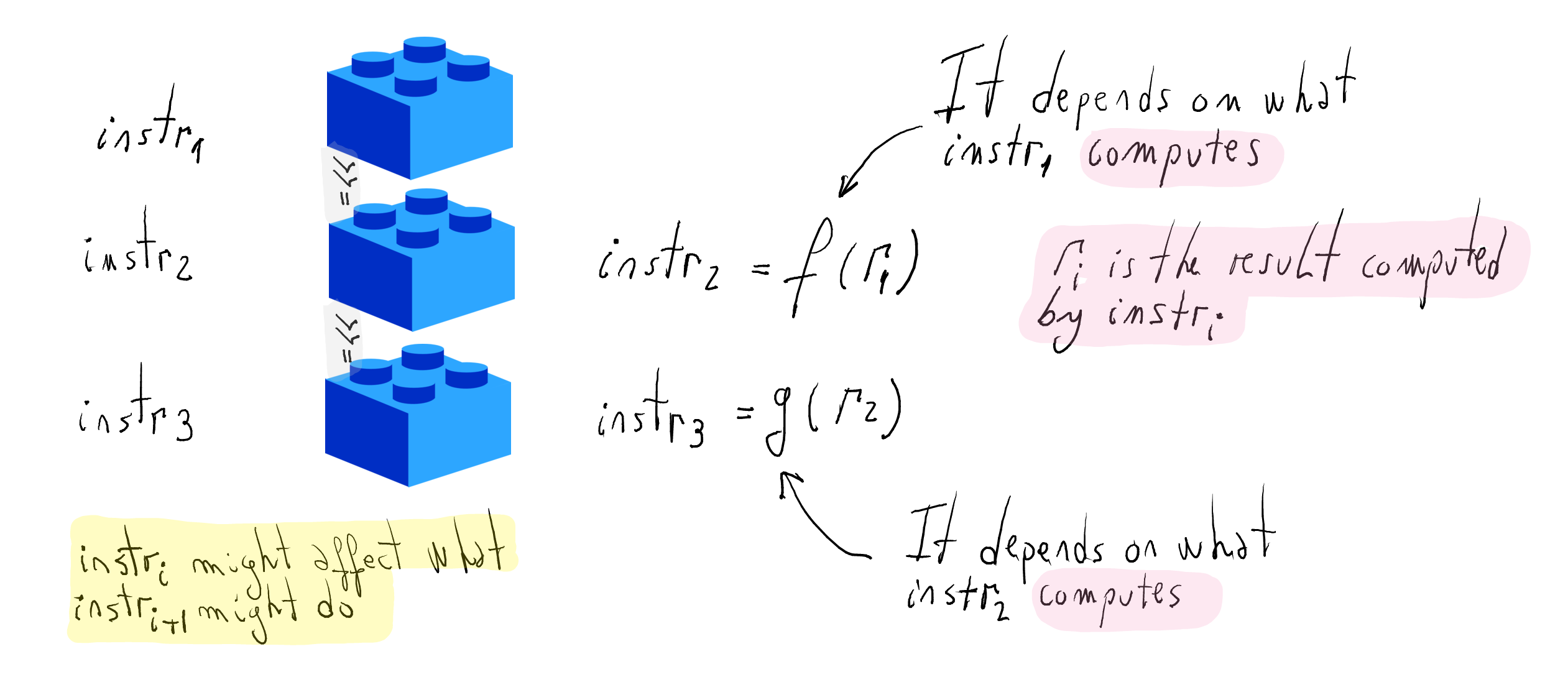
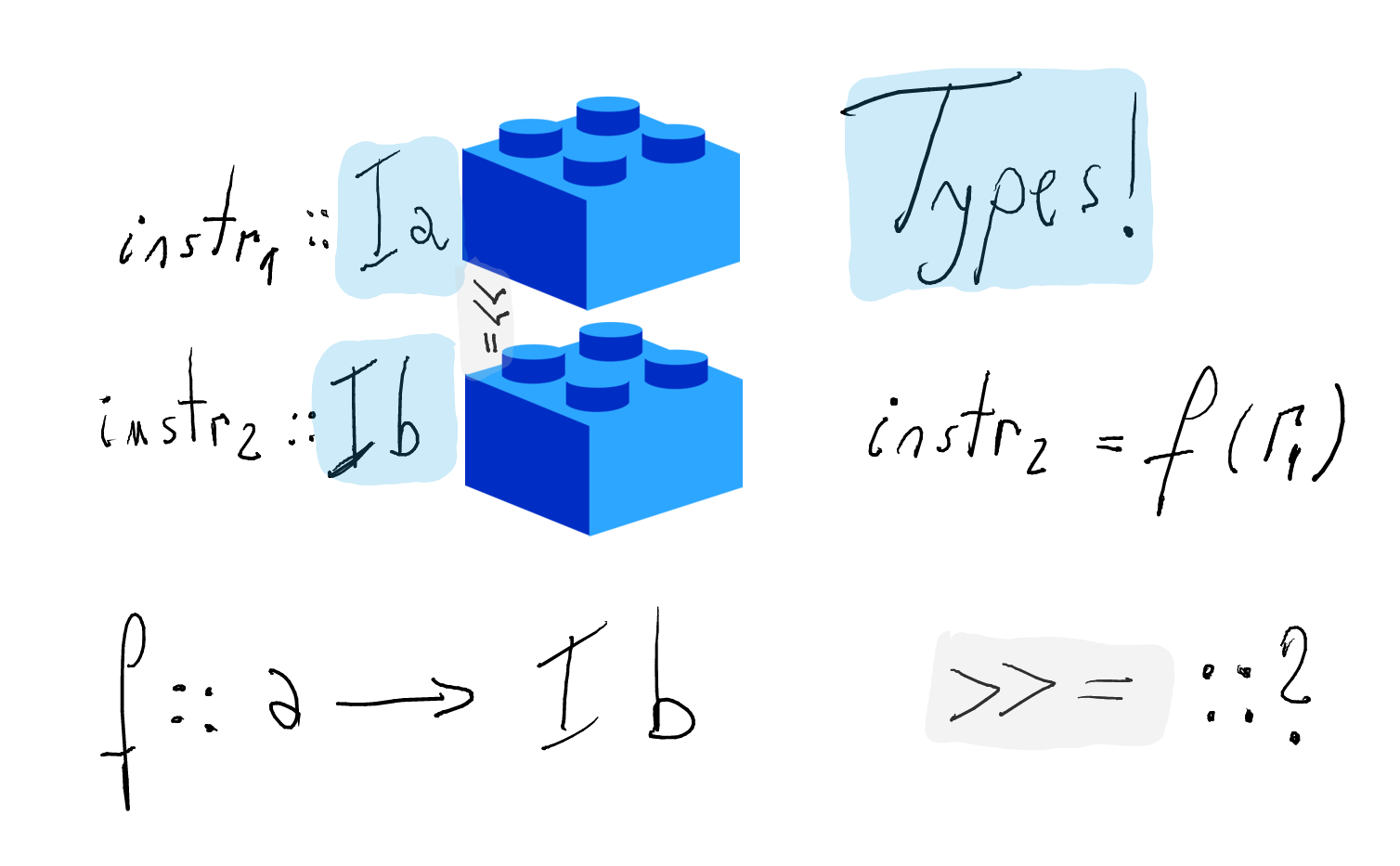
Functions f(r1) and g(r2) encode the dependency among instructions.
What are the types for f and g, respectively?
- Let us first introduce the types for instructions.
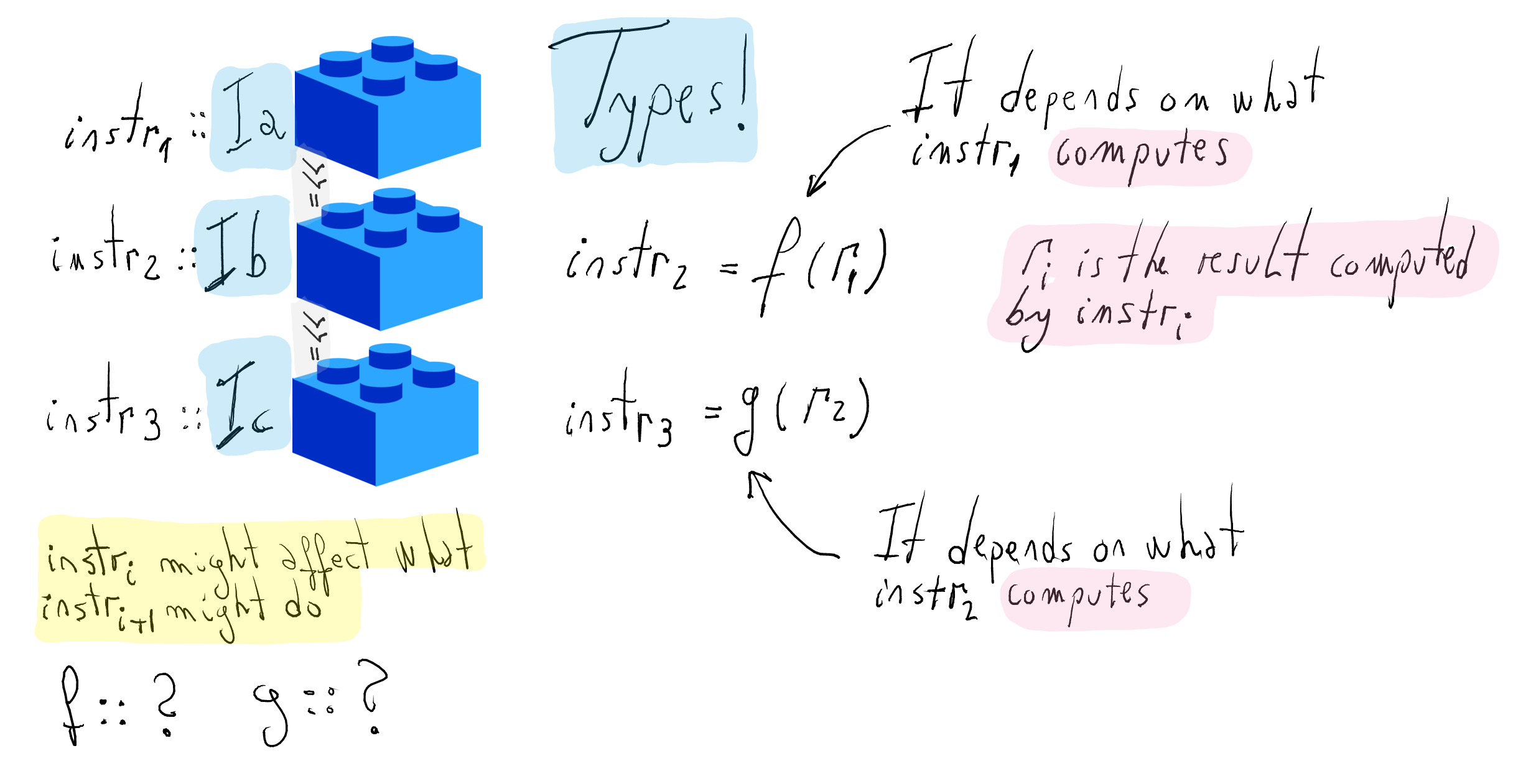
What is the type of the connector (>>=)?

Error handling

The connector is placed in the "right place" to abort any computation as soon as an instruction fails
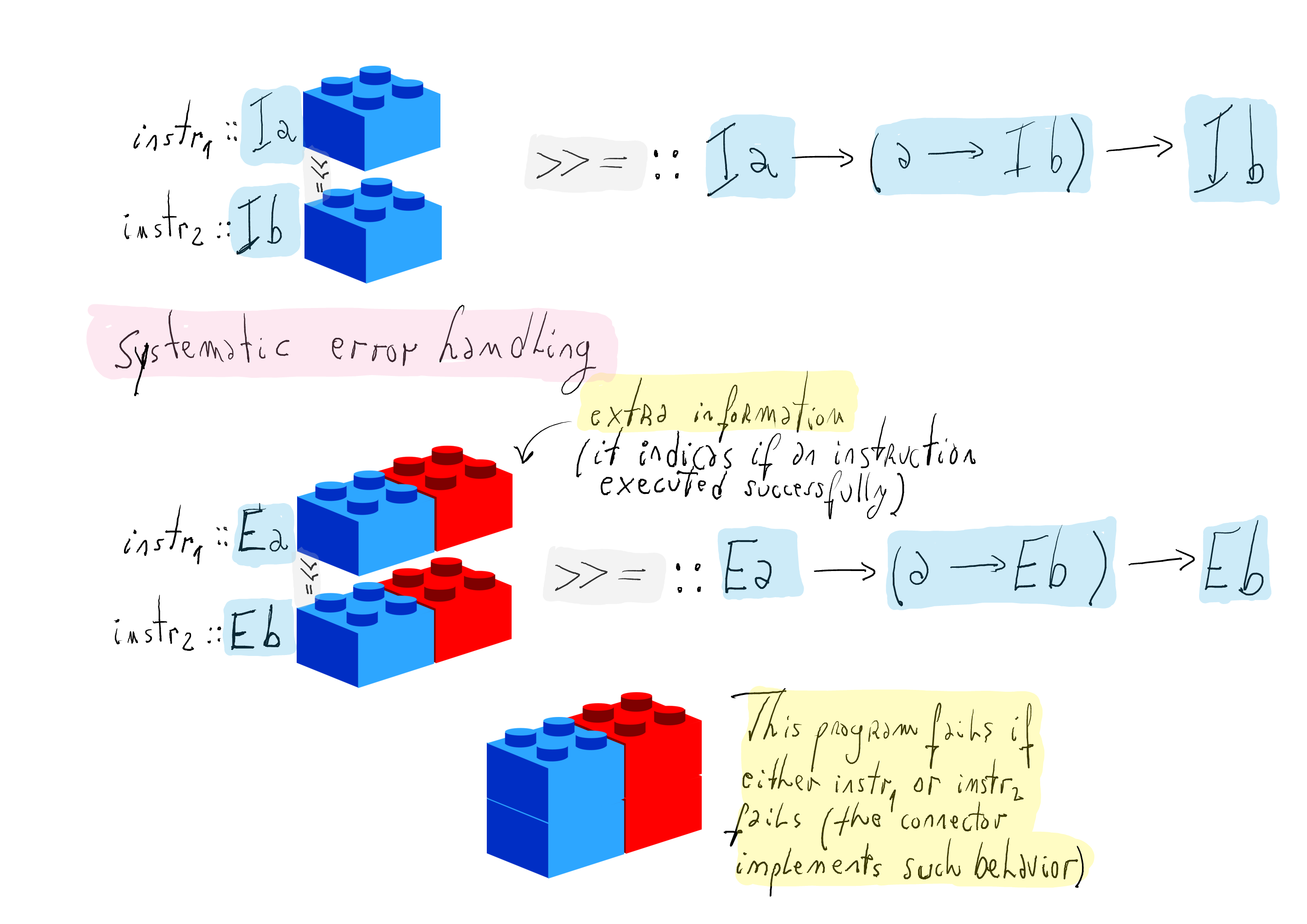
A data type for handling errors
```
data E a = Value a | Wrong
```
Is E a a monad? Is E a such special data type?
- Not yet, we need to define the connector (>>=)
- Furthermore, monads have another primitive: return. This primitive takes a value and constructs an instruction that does nothing but producing that value!

In Haskell, a data type is a monad if return and (>>=) are provided

  class Monad m where
     return :: a -> m a
     (>>=)  :: m a -> (a -> m b) -> m b

What is the implementation of return and (>>=) for E a?

  instance Monad E where
    return = Value
    Wrong   >>= f = Wrong
    Value a >>= f = f a

Monad E is known as the Maybe monad!

We need to add a primitive to make everything fail
```
abort :: E a
abort = Wrong
```
This function is known as a non-proper morphism. In other words, non-proper morphisms are operations which are not return and (>>=). They handle or affect the side-effectful part of the computation (in the case above, the failure!)

One possible run function

 m_runE :: Expr -> IO ()
 m_runE e = case m_interpE e of
                 Wrong -> putStrLn "Something went wrong!"
                 Value i -> putStrLn $ show i

It did not change much as the non-monadic version

Error handling in the interpreter

Let us rewrite the interpreter using the monad E

 m_interpE :: Expr -> E Int
 m_interpE (Con i)     = return i
 m_interpE (Div e1 e2) = m_interpE e1 >>= (\i1 ->
                           m_interpE e2 >>= (\i2 ->
                             if i2 == 0 then abort
                                        else return (i1 `div` i2)))

Observe that the code has minimum traces of error handling, i.e., it does not inspect every recursive call for an error.
- It is handled by the monad!
- All the plumbing is hidden!

Let us remove some parenthesis due to the connector (>>=) precedence

 m_interpE :: Expr -> E Int
 m_interpE (Con i)     = return i
 m_interpE (Div e1 e2) = m_interpE e1 >>= \i1 ->
                           m_interpE e2 >>= \i2 ->
                             if i2 == 0 then abort
                                        else return (i1 `div` i2)

Logging

We would like to be able to control what information gets logged
We want to implement the side-effect of logging, i.e., the program computes the result of arithmetic expressions and, as a side-effects, generates a log of messages.

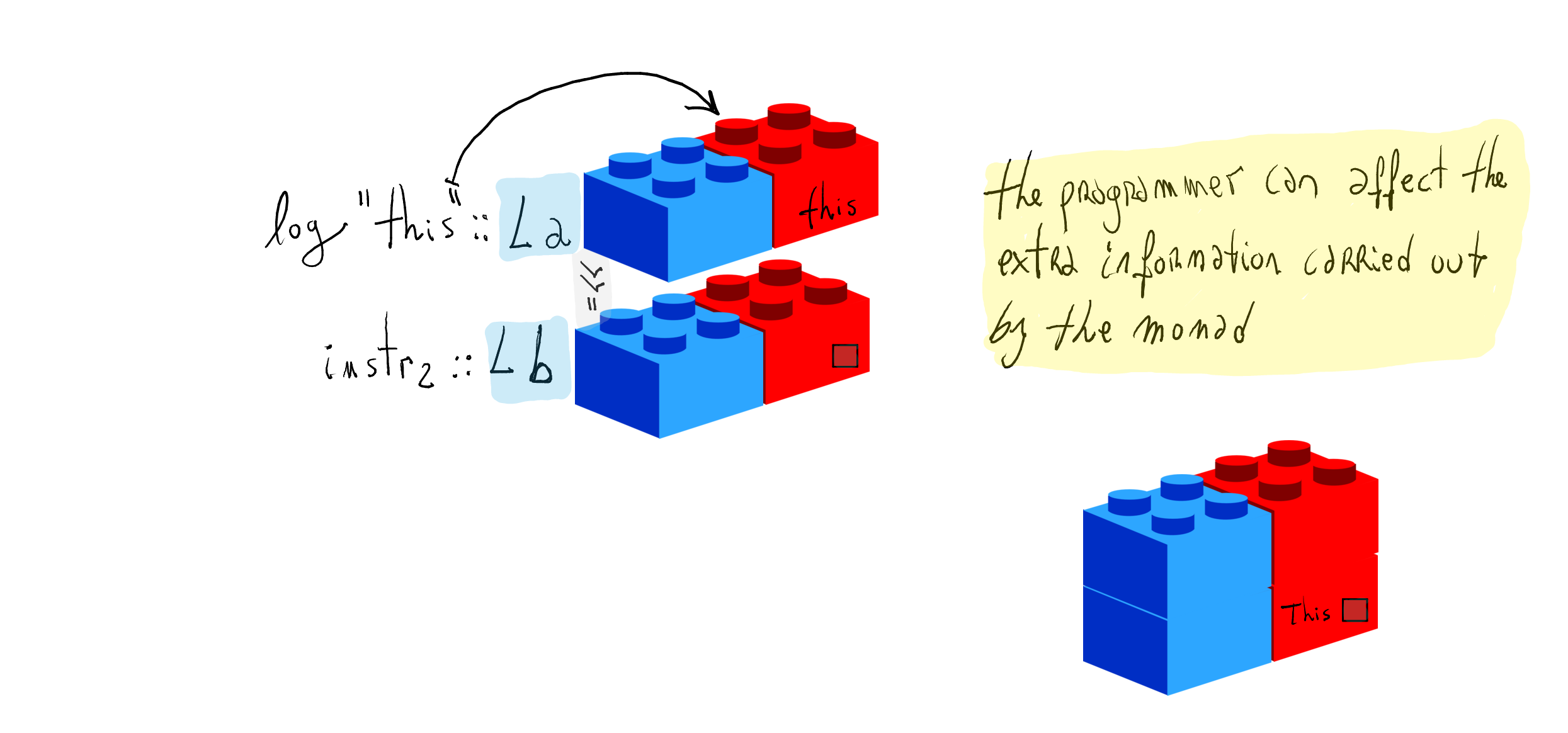
Let us define return and (>>=) for L

 instance Monad L where
   return x   = L (x, [])  -- recall the identity laws!
   L (x,msgs) >>= f = case f x of
                      L (x,msgss) -> L (x, msgs ++ msgss)

Function return produces the empty lists (recall the monadic laws)
Function (>>=) concatenates the logs

We need to implement a non-proper morphism which writes into the log -- we call it msg
```
msg :: String -> L ()
msg m = L ((), [m]) 
```

Let us rewrite the interpreter using the monad L

 m_interpL (Con i) = do
     msg "-- Hit Con --\n"
     return i

 m_interpL (Div e1 e2) =
    msg "-- Hit a Div --\n" >>= \_ ->
        msg "** Left recursive call**\n" >>= \_ ->
           m_interpL e1 >>= \i1 ->
              msg "** Right recursive call**\n" >>= \_ ->
                  m_interpL' e2 >>= \i2 ->
                        return (i1 `div` i2)

Observe that the code has minimum traces about how the log is constructed
- It is handled by the monad!
- All the plumbing is hidden!
- It looks like imperative programming!
Observe that we use many times m >>= \_ -> ... when m does not produce a useful value for the computation but a useful side-effect! (in this case, logging)
- Monads use the operation (>>), called blind, to capture such situation and save us from writing functions which ignore arguments.
```
(>>) :: m a -> m b -> m b
m1 >> m2 = m1 >>= \_ -> m2 
```
  Observe that function (>>) is a derived operation.

Let us rewrite the interpreter once more

 m_interpL (Div e1 e2) =
    msg "-- Hit a Div --\n" >>
        msg "** Left recursive call**\n" >>
           m_interpL e1 >>= \i1 ->
              msg "** Right recursive call**\n" >>
                  m_interpL e2 >>= \i2 ->
                        return (i1 `div` i2)

One possible run function

m_runL :: Expr -> IO ()
m_runL e = do  putStr "Result: "
               putStrLn $ show result
               putStrLn "Messages:"
               putStrLn $ concat log
   where L (result,log) = m_interpL e

Enter Monads

Definition

A data type m is a monad if it supports the following two operations:
```
(>>=)  :: m a -> (a -> m b) -> m b
return :: a -> m a 
```
Functions return and (>>=) are known as return and the bind operations, respectively.

Furthermore, these operation are required to fulfill the next laws:
Name Law
Left identity:
return a >>= f ≡ f a
Right identity:
m >>= return ≡ m
Associativity:
(m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)
Exercise: Check that E and L respects these laws.
Terminology
- Monadic simply means pertaining to monads.
  - A monadic type M means that it is an instance of the Monad type class; a monadic value has a monadic type.
Notation

Writing code with the bind might be unfamiliar and it requires indentation at every application of (>>=) to keep the code readable.
```
m1 >>= \r1 ->
   m2 >>= \r2 ->
      m3
```
Haskell supports do-notation, a more familiar manner to write monadic code.
```
do r1 <- m1
   r2 <- m2
   m3
```
Similarly,
```
m1 >>
  m2 >>= \r2 ->
     m3
```
can be written as
```
do m1
   r2 <- m2
   m3
```

Name	Law
Left identity:	return a >>= f ≡ f a
Right identity:	m >>= return ≡ m
Associativity:	(m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)

Revised interpreters

Error handling

m_interpE :: Expr -> E Int
m_interpE (Con i)     = return i
m_interpE (Div e1 e2) =
   do i1 <- m_interpE e1
      i2 <- m_interpE e2
      if i2 == 0 then abort
                else return (i1 `div` i2)

Logging

m_interpL :: Expr -> L Int
m_interpL (Con i)     = do
   msg "-- Hit Con --\n"
   return i

m_interpL (Div e1 e2) = do
   msg "-- Hit a Div --\n"
   msg "** Left recursive call**\n"
   i1 <- m_interpL e1
   msg "** Right recursive call**\n"
   i2 <- m_interpL e2
   return (i1 `div` i2)

It looks and feel like imperative programming (but it is not!)
Monads alleviate all the explicit data flow required to implement error handling and logging.

Monads and EDSL?

In our examples above, we talk about monadic types, constructors, combinators, non-proper morphisms, and run functions
```
-- Types
data E Expr
-- Constructors
return :: a -> E Expr
abort  :: E Expr
-- Combinators
(>>=) :: E Expr -> (a -> E Expr) -> E Expr
-- Run function
m_runE :: Expr -> IO()
```
The type E and monadic operations return and (>>=) are polymorphic; in fact, monads require them to be (recall the type class Monad). However, when instantiate them to the type that we are interested in, i.e., in this case Expr, we have a EDSL!
Monads are also useful to define EDSL in Haskell, but not every EDSL is necessarily a monad!
Are monads E and L shallow or deep embeddings?
- Shallow!
```
 data E a = Value a | Wrong
```
  An expression of type E a is either a value or indicates that something went wrong! It denotes its semantics! The same phenomenon occurs with L a.

Deep embedding for error handling monad

We start defining our data type
```
data E_deep a where
   -- Constructors
   Return :: a -> E_deep a
   Abort  :: E_deep a
   -- Combinators
   Bind   :: E_deep a -> (a -> E_deep b) -> E_deep b
```
To implement this data type, we need to tell GHC to use the GADTs extension by adding
```
{-# LANGUAGE GADTs #-}
```
at the beginning of the file. We will study more about GADTs in the course, but so far just notice the definition of Bind. It returns E_deep b although the data type is defined on E_deep a -- this is one of the key features of GADTs!

The definition for return, (>>=), and non-proper morphisms are trivial

 instance Monad E_deep where
    return = Return
    (>>=) = Bind

 abort_deep = Abort

The run function is the interesting one.

 run_deep :: Expr -> IO ()
 run_deep e = case (to_semantics (interp_deep e)) of
                 Wrong -> putStrLn "Something went wrong!"
                 Value i -> putStrLn $ show i
   where
         -- It will not accept E_deep Int -> E Int due to Bind
         to_semantics :: E_deep a -> E a
         to_semantics (Return i) = Value i
         to_semantics  Abort     = Wrong
         to_semantics (Bind m f) = case to_semantics m of
                                        Wrong   -> Wrong
                                        Value i -> to_semantics (f i)

Stateful computations

There is no more imperative feature like having a global state and transforming it during a computation
Imagine that we want to count the number of division in our interpreter
- This could be useful for future optimization

Assuming that we have a unique global counter, we would like to have a code like the following:

 interpS (Con i)     = return i
 interpS (Div e1 e2) = do
    i1 <- interpS e1
    i2 <- interpS e2
    -- Read the global counter
    dvs <- get
    -- Increment it by one
    put (dvs+1)
    return (i1 `div`i2)

We start by describing the type for stateful computations
```
data St s a
```
A monadic expression of type St s a denotes an stateful computation, with state of type s, which produces a value of type a.

The monad here is St s!
Besides return and (>>=), do we need non-proper morphisms?

Yes! To control the side-effects, i.e., to read and write the state.
```
get :: St s s
put :: s -> St s ()
```
Observe that get returns the state as a value, while put returns () since it does not produce any value but modifies the state.

To summarize, we have the following interface for stateful computations.

-- Type
data St s a
-- Constructors
get    :: St s s
put    :: s -> St s ()
return :: a -> St s a
-- Combinators
(>>=)  :: St s a -> (a -> St s b) -> St s b

Implementation (shallow embedding)

Semantics for stateful computations

What is the semantics of an instruction which can read and modify a given state?
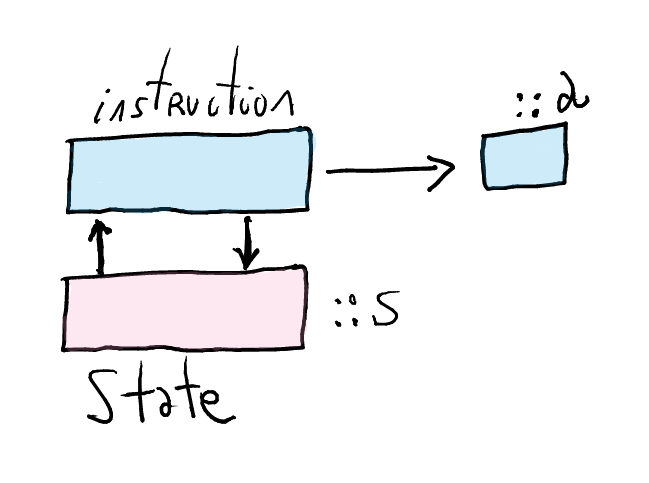
An instruction produces some result, but also read or write into the state.
Separating the reading and writing actions in the state, we can draw the graphic above as follows
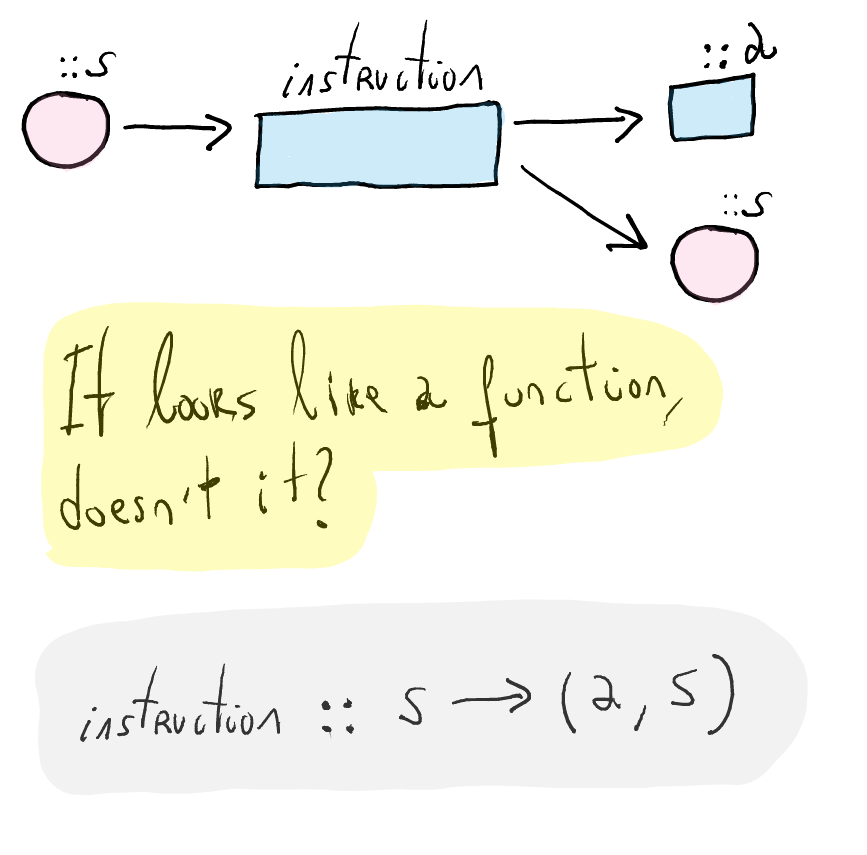
An instruction in the state monad is a function!
- This reflects the fact that it depends on the state
A program, i.e., a sequence of instructions built with the monadic operations, is also a function of type s -> (a, s).
More concretely,
```
 data St s a = MkSt (s -> (a,s))

 get :: St s s
 get = MkSt $ \s -> (s,s)

 put :: s -> St s ()
 put s = MkSt $ \_ -> ((),s)

 instance Monad (St s) where
   return x       = MkSt $ \s -> (x,s) 
```
Function get just places the state (receiving as an argument) as the result of the computation. Function put ignores the state given as an argument and sets the one given as an argument. Operation return does not change the state and produces as a result its argument.

What about (>>=)?

The definition of (>>=) is responsible of passing along the state from one instruction to the other.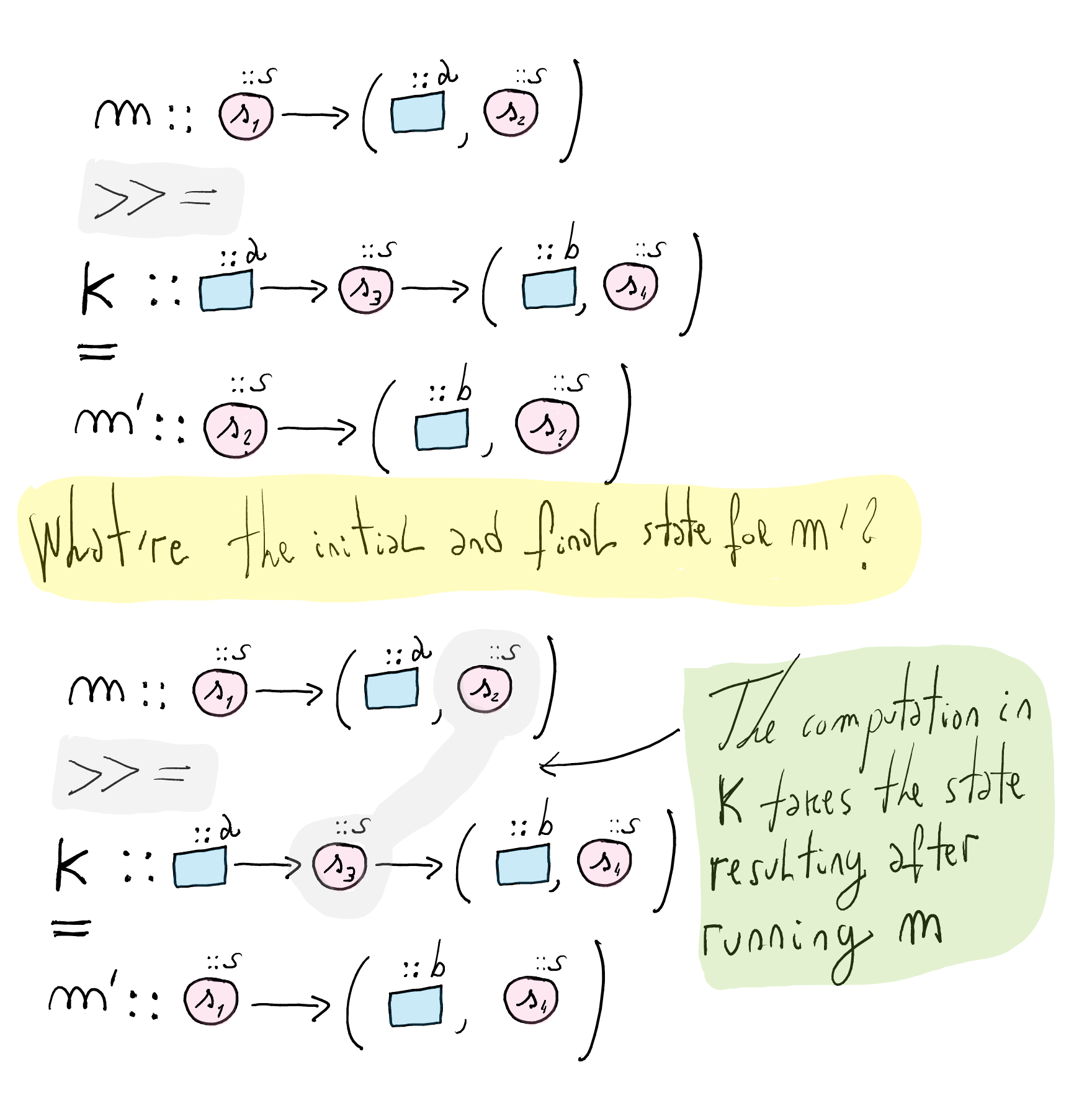

(MkSt m) >>= k = MkSt $ \s_1 -> let (a, s_2) = m s_1
                                    MkSt k_m = k a
                                in k_m s_2

A possible run function

 m_runS :: Expr -> IO ()
 m_runS e = do
    putStr "Result: "
    putStrLn $ show result
    putStrLn "Number divisions:"
    putStrLn $ show final_st

    where MkSt f = interpS e
          (result,final_st) = f 0

Monads so far

Imperative side-effects
- Error handling
- Logging
- State
The concept of monads goes beyond that
- Security
- Probability programming
- Non-determinism
- Software transnational memory
We will see more of these monads later in the course.
What about combining effects?
- State, error, and logging!
- Next lecture