Type-based modeling & looking back!
Type-based modeling
- In this lecture, we will see some advanced type-system features for Haskell
Most advanced type-system features are introduced for two purposes
- Typing more well-behaved programs
- Typing less bad-behaved programs
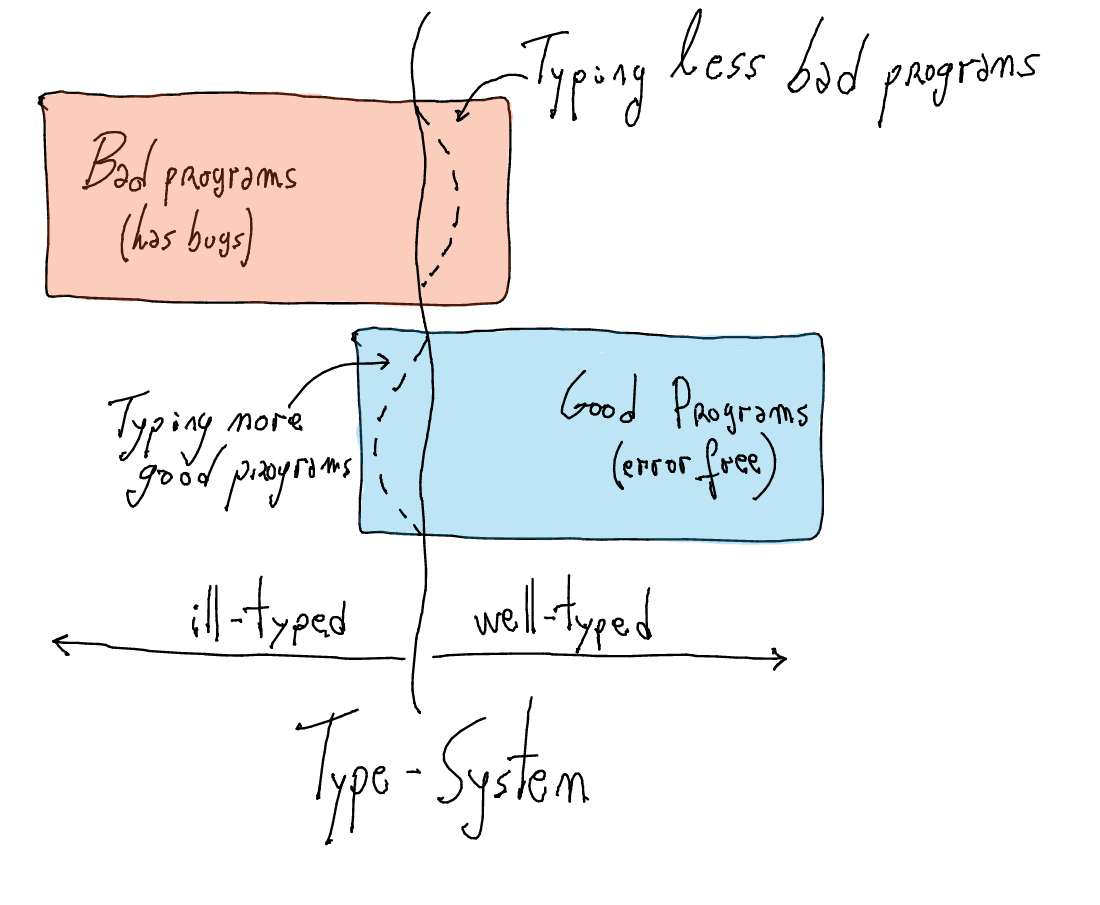
Typing more well-behaved programs
In Haskell, the addition has the following signature
(+) :: Num a => a -> a -> a
This allows any numeric type to be used for addition as long as both arguments have the same type.
In math, it is common to allow addition of, for example, integers and real numbers.
Defining a more flexible addition is a nice little exercise to introduce associated types (type families).
In principle, there is no reason for not typing the following expression
(1 :: Int) + (2.5 :: Float)
A good implementation for "this"
(+)requires to "cast" the left-side argument to a float and then perform the sum.
Associated types
What is the type of
(+)?(1 :: Int) + (2.5 :: Float)
In this case, we have that
(+) :: Int -> Float -> Float
If we have other arguments,
(1.5 :: Double) + (2.1 :: Float)
Then, we have that
(+) :: Double -> Float -> Double
The resulting type of
(+)depends on the type of the arguments.When there are dependencies, there are chances to use functions!
If you think
Fas a function on types, we can give the type signature of(+)as follows.(+) :: a -> b -> F a b
An associate type is a function at the level of types
class Add a b where -- uses MultiParamTypeClasses type F a b -- uses TypeFamilies as well add :: a -> b -> F a b
Roughly speaking, functions at the type level require the
TypeFamiliesextension.Where do we give the definition of
F?In the type class instances!
instance Add Integer Double where type F Integer Double = Double -- defining F add x y = fromIntegral x + y instance Add Double Integer where type F Double Integer = Double -- defining F add x y = x + fromIntegral y
As for
(+), we defineaddfor arguments of the same type.instance (Num a) => Add a a where -- uses FlexibleInstances type F a a = a add x y = x + y
We can even define addition between a number and a list (of integer, float, etc.).
instance (Add Integer a) => Add Integer [a] where -- uses FlexibleContexts type F Integer [a] = [F Integer a] add x ys = map (add x) ysNow, we can safely add elements of different types
test = add (3::Integer) (4::Double) aList :: [Integer] aList = [0,6,2,7] test2 :: [Integer] test2 = add (1::Integer) aList test3 :: [Double] test3 = add (38::Integer) [1700::Double]
Typing less bad-behaved programs
Type-systems are not perfect!
We can still write well-typed programs which fail at runtime. They do not fail due to a type-error, but rather a problem in its semantics.
Type-systems ensure that no type-error are raised at runtime, but they do not say anything about other type of errors programs might have> head [] *** Exception: Prelude.head: empty list > [1,2,3] !! 5 *** Exception: Prelude.(!!): index too large
We would like our type-system to help us out to rule out such programs
For that, we are going to encode more of our functions invariants into the types.
For instance, in the example above, the type of a list indicates its length.
[1,2,3] :: Vector 3 Int
Having the length as part of the type, we can now impose a restriction on the function accessing to elements of a list.
(!!) :: (n <= m) => Vector n Int -> m -> Int
Haskell does not have a strong enough type-system (e.g., like Agda) to encode the type of lists and
(!!)exactly as described above. However, we will get very "similar" types by using several extensions.
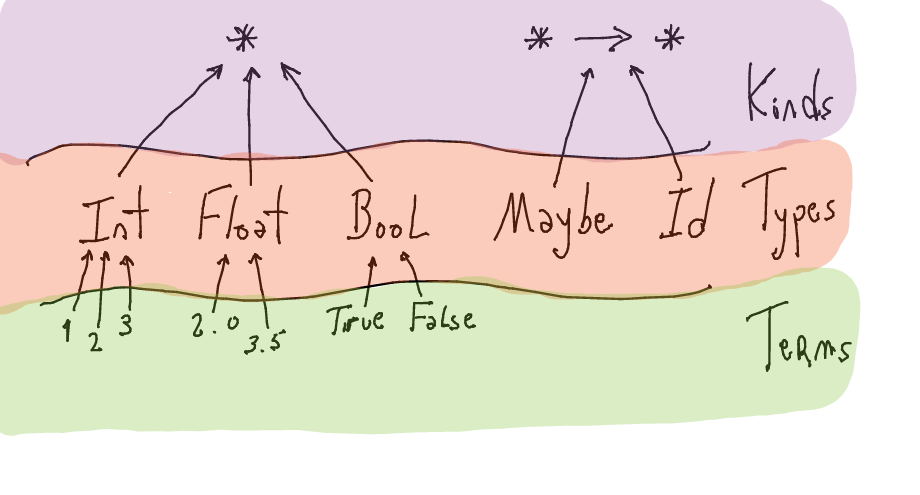
Kinds
Kinds are the
type of typesHaskell has the kind
*, the type of all the typesInt :: * Bool :: * Char :: * Char -> Bool :: * (Char, Bool) :: *
What about type operators? (e.g.,
Maybe,[])A type operator is essentially a type-level constructor which generates a type based on its argument(s).
Maybe :: * -> * [] :: * -> * (->) :: * -> * -> *
The kind of type operators describes the amount of type arguments required to produce a type. For instance,
Maybeis waiting for a single type, soMaybe Bool :: *produces a type for optional boolean values. Similarly,(->) a b :: *produces the type of functions going fromatob.Revisiting monad transformers, we have that
StateT :: * -> (* -> *) -> * -> *
Observe that the second kind argument is a type constructor, i.e., the monad to apply the transformer.
Kinds take us one level up in the organization of Haskell's abstractions
Data kinds
To express invariants at the level of types, we would like to talk about values as types.
For instance,
(!!) :: m <= n => ...
We are thinking about the values
mandnas types instead.The extension
DataKindsautomatically promotes every suitable datatype to be a kind and its constructors to be types/type constructors.Let us take as an example natural numbers
data Nat where Zero :: Nat Suc :: Nat -> NatWith DataKinds, we have the following kinds and types/type constructors (with no inhabitants but
undefined).
Once we have kinds, we can use them to restrict the types used in a GADT. In our example, we are going to denote the length of a vector with a type-level natural.
data Vector a (n :: Nat) where -- uses KindSignatures Nil :: Vector a Zero (:-) :: a -> Vector a n -> Vector a (Suc n)
Now, we can write
array :: Vector Int (Suc (Suc Zero)) array = 2 :- (1 :- Nil)
Observe that we cannot write an array which length is not properly captured by the types. The following expressions are ill-typed.
array2 :: Vector Int (Suc (Suc Zero)) array2 = (1 :- Nil)
By using the data kindNatin the GADT, we capture the length of lists in the types!We are going to keep this fact as an invariant for every built vector.
Type families
What if we need to append two existing arrays? What is the length of the resulting data?
We need to compute its length at the type-level, i.e., at compile time!
append :: Vector n a -> Vector m a -> Vector a ?
Which type should I use? Clearly, it should be the type that represents the "sum" of types
nandm.We would like to compute the length (type) of the resulting array as a function on the types
nandm.append :: Vector n a -> Vector m a -> Vector a (Sum n m)
Function
Sumneeds to get evaluated at compile-time!Instead of using
Sum, we can use more fancy notation.append :: Vector n a -> Vector m a -> Vector a (n :+: m)
How can we define such type-level functions?
Type families are type-level functions, which come in two flavors (opened and closed)
In this course, we are going to use closed typed families
A type family is closed when all its equations are given in the same module. It is then easier for GHC to manipulate them -- it does not need to assume that its definition might be extended so it can aggressively apply it when encounter one.
Adding type-level natural numbers
type family (n :: Nat) :+: (m :: Nat) :: Nat -- uses TypeOperators, -- TypeFamilies type instance Zero :+: m = m type instance (Suc n) :+: m = Suc (n :+: m)We can complete the definition for
appendas followsappend :: Vector a n -> Vector a m -> Vector a (n :+: m) append (x :- xs) ys = x :- append xs ys append Nil ys = ys
Data kinds and type-classes
The point of having the
Vector a nas a type is to rule out invalid accesses to its elements at compile time.Recall the example we started with.
> [1,2,3] !! 5 *** Exception: Prelude.(!!): index too large
What should it be the type of
indexif used on elements of typeVector a n?In an ideal world, it would be as follows.
index :: LessEq n m => (n :: Nat) -> Vector a (Suc m :: Nat) -> a
(We explain below by
Suc minstead ofm.)Unfortunately, this type is not a valid type in Haskell. There are many problems with it.
First, we cannot use data kinds to build function types. Recall that
(->) :: * -> * -> *, so(n :: Nat) -> ..is ill-typed sincenhas kindNatand not*.We remove
n :: Natfrom the ideal type.index :: LessEq n m => ...n... -> Vector a (Suc m :: Nat) -> a
Observe that we still need
nsince it is used by the the type classLessEq n m.
Constraint
LessEq n mholds when the type-level naturalnis less or equal thanm.index :: LessEq n m => ...n... -> Vector a (Suc m :: Nat) -> a
If we consider
array(see its definition above) of sizeSuc (Suc Zero), thenncan be eitherZeroorSuc Zero. Recall that indexes start from0for accessing elements in lists by using(!!)-- that is why we haveSuc min the type rather than justm.We define this type-class in the usual way, but using data kinds.
class Less (n :: Nat) (m :: Nat) where -- uses MultiParamTypeClasses
First, we declare that the
Zerotype is less or equal than any other type-level natural.instance Less (Zero :: Nat) m where -- uses FlexibleInstances
Then, we define the case for non-zero type-level naturals.
instance Less n m => Less (Suc n :: Nat) (Suc m :: Nat) where
Observe that the type-classes are empty (i.e., they contain no methods).
Forgetting types
Let us consider what happens when we try to implement
indexindex :: Less n m => ...n... -> Vector a (Suc m :: Nat) -> a index tn vec = ... !! ...
We want to use
(!!)from lists. So, we need to "cast" a vector into a list. This is usually not a problem; after all, forgetting types is not difficult.toList :: Vector a n -> [a] toList Nil = [] toList (x :- xs) = x:toList xs
We can then complete the definition of
indexa little bit more.index :: Less n m => ...n... -> Vector a (Suc m :: Nat) -> a index tn vec = (toList vec) !! ...
Singleton types
In the implementation of
index, the second argument for(!!)depends on the type oftn.For instance, if
nhas typeZero, the argument needs to be0. Instead, ifnhas typeSuc (Zero), then the argument needs to be1.In other words, for any type-level
n, there should be a term-level representation for it. This correspondence can be established using singleton types.By definition of data promotion, any type
nsuch thatn :: Nathas no inhabitants exceptundefined. Therefore, it is impossible to establish a one-to-one correspondence between types and term-level representations.Instead, we declare a new inhabited data type which takes types of kind
Natdata SNat (n :: Nat) where SZero :: SNat Zero SSuc :: SNat n -> SNat (Suc n)Observe that for any type
SNat (n :: Nat), there exists one term which inhabits such type (besidesundefined). For instance, if a termthas typeSNat Zero, thenthas the formSZero. Similarly, if a termthas typeSNat (Suc (Suc Zero)), thentis of the formSSuc (SSuc SZero).Having the type
SNat (n :: Nat), we can write a function which synthesizes a term-level integer based on the type-leveln :: NattoNat :: SNat n -> Int toNat SZero = 0 toNat (SSuc n) = 1 + toNat n
Using function
toNat, we can complete the implementation ofindexindex :: Less n m => SNat n -> Vector a (Suc m :: Nat) -> a index tn vec = (toList vec) !! (toNat tn)
Examples
Let us define some indexes of type
SNat (n :: Nat)for some type-level indexn.zero = SZero one = SSuc SZero two = SSuc (SSuc SZero)
Accessing valid indexes in arrays type-checks!
> index zero array 2 > index one array 1 > index two array No instance for (Less ('Suc 'Zero) 'Zero) ...
Summary
Typing more well-behaved programs
Associated types
- Typing more well-behaved programs
- Used with type-classes
- It is a type level functions (i.e., type family)
Typing less bad-behaved programs
Kinds
- The "type" of types
- Data kinds (lifting data types and their elements "one level up")
Type families
- Type-level functions
Singleton types