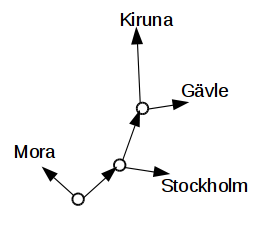
middleOfNowhere :: Road
middleOfNowhere =
Fork
( City "Mora" )
( Fork
( Fork
( City "Kiruna" )
( City "Gävle" )
)
( City "Stockholm" )
)
| DAY: January 3, 2015 | TIME: 08:30–12:30 | PLACE: V-salar |
|
Responsible: Aids: Grade: |
Emil Axelsson, D&IT, Tel: 0733-701736 An English (or English-Swedish, or English-X) dictionary
Completing Part I gives a 3 or a G; |
|
Part I (5 small assignments)
|
Part II (2 larger assignments)
|
| Please read the following guidelines carefully: |
Part I
You have to complete 4 out of the following 5 assignments to get a pass on the exam.
1. Implement a function
occurs :: Eq a => a -> [a] -> Intthat given an x and a list xs, finds out how often x occurs in the list.
Examples:
*Main> occurs 'a' "bepacepadepa"
3
*Main> occurs 11 [2,3,5,7,11,13,7,5]
1
*Main> occurs "hej" ["hi","hola","hello","hoi"]
02. Implement a function
urls :: String -> [String]that given a text (as a string), returns a list with all web addresses (URLs) in that text. We say that web addresses are words that start with the string “http://”.
Examples:
*Main> urls "I tried loading http://www.chalmers.se and http://www.google.com but I didn't succeed."
["http://www.chalmers.se","http://www.google.com"]
*Main> urls "It's fun to stay at the Y.M.C.A."
[]Hint:
isPrefixOf. The expression isPrefixOf p s checks whether the string s begins with the string p.words and filter.3. Consider the following recursive data type which represents roads:
data Road
= City String
| Fork Road RoadCity c represents a road that goes straight to the city c.
Fork l r represents a road on which turning left leads to another road l and turning right leads to the road r.
Here is an example road and the corresponding map:
|

|
Now, implement a function
reachable :: String -> Road -> Boolthat checks whether a given city is reachable from the given road.
Examples:
*Main> reachable "Kiruna" middleOfNowhere
True
*Main> reachable "Jukkasjärvi" middleOfNowhere
FalseHints:
Road can be reached from the root, checking whether a city is reachable is the same as checking whether it is included in the Road.4. Write a QuickCheck property that expresses the fact that nub never returns a list that is longer than its argument.
5. Write a function
copyFile :: FilePath -> FilePath -> IO ()which takes two file names, and copies the contents of the first file to the second file.
Example:
*Main> readFile "apa.txt"
"abracadabra"
*Main> copyFile "apa.txt" "bepa.txt"
*Main> readFile "bepa.txt"
"abracadabra"Hint:
6. Herman is implementing a car navigation system for Android devices. As the internal representation of maps, he decided to use the Road data type from assignment 3. One part of the system’s functionality is to be able to present a list of directions given a current position and a destination. The car’s current position is represented as a value of type Road, and the result of the navigation system is a list of “turns”, where a turn is either left or right:
data Turn = L | R deriving (Show)Implement the function roadMap which generates the list of directions to reach a given city:
roadMap :: String -> Road -> Maybe [Turn]A call to this function takes the form roadMap city pos, where city is the destination city and pos is the car’s current position.
Examples:
*Main> roadMap "Stockholm" middleOfNowhere
Just [R,R]
*Main> roadMap "Kiruna" middleOfNowhere
Just [R,L,L]
*Main> roadMap "Tanum" middleOfNowhere
Nothing7. In this assignment, you will implement a text processing function called fill that fills paragraphs of text. Your function will take two arguments: (1) an integer indicating the line width of the text, and (2) a list of words. It should then produce a list of lines (the text) containing all the words in the right order, but not exceeding the specified line width.
The type of the function is thus:
fill :: Int -> [String] -> [String]
-- width words linesHere are two examples of its use, demonstrating the effect of line widths 35 and 50 on the same text (taken from the Wikipedia entry on cats):
*Main> do s <- readFile "wp_cats.txt"; putStr (unlines (fill 35 (words s)))
The cat (Felis catus), also known
as the domestic cat or housecat to
distinguish it from other felids
and felines, is a small, usually
furry, domesticated, carnivorous
mammal that is valued by humans for
its companionship and for its
ability to hunt vermin and
household pests.
*Main> do s <- readFile "wp_cats.txt"; putStr (unlines (fill 50 (words s)))
The cat (Felis catus), also known as the domestic
cat or housecat to distinguish it from other
felids and felines, is a small, usually furry,
domesticated, carnivorous mammal that is valued by
humans for its companionship and for its ability
to hunt vermin and household pests.Hint:
split :: Int -> [String] -> ([String],[String]) that splits a list of words into two lists, the first list being just enough words that fit on one line.Appendix
{-
This is a list of selected functions from the standard Haskell modules:
Prelude
Data.List
Data.Maybe
Data.Char
-}
--------------------------------------------------------------------------
-- standard type classes
class Show a where
show :: a -> String
class Eq a where
(==), (/=) :: a -> a -> Bool
class (Eq a) => Ord a where
(<), (<=), (>=), (>) :: a -> a -> Bool
max, min :: a -> a -> a
class (Eq a, Show a) => Num a where
(+), (-), (*) :: a -> a -> a
negate :: a -> a
abs, signum :: a -> a
fromInteger :: Integer -> a
class (Num a, Ord a) => Real a where
toRational :: a -> Rational
class (Real a, Enum a) => Integral a where
quot, rem :: a -> a -> a
div, mod :: a -> a -> a
toInteger :: a -> Integer
class (Num a) => Fractional a where
(/) :: a -> a -> a
fromRational :: Rational -> a
class (Fractional a) => Floating a where
exp, log, sqrt :: a -> a
sin, cos, tan :: a -> a
class (Real a, Fractional a) => RealFrac a where
truncate, round :: (Integral b) => a -> b
ceiling, floor :: (Integral b) => a -> b
--------------------------------------------------------------------------
-- numerical functions
even, odd :: (Integral a) => a -> Bool
even n = n `rem` 2 == 0
odd = not . even
--------------------------------------------------------------------------
-- monadic functions
sequence :: Monad m => [m a] -> m [a]
sequence = foldr mcons (return [])
where mcons p q = do x <- p; xs <- q; return (x:xs)
sequence_ :: Monad m => [m a] -> m ()
sequence_ xs = do sequence xs; return ()
--------------------------------------------------------------------------
-- functions on functions
id :: a -> a
id x = x
const :: a -> b -> a
const x _ = x
(.) :: (b -> c) -> (a -> b) -> a -> c
f . g = \ x -> f (g x)
flip :: (a -> b -> c) -> b -> a -> c
flip f x y = f y x
($) :: (a -> b) -> a -> b
f $ x = f x
--------------------------------------------------------------------------
-- functions on Bools
data Bool = False | True
(&&), (||) :: Bool -> Bool -> Bool
True && x = x
False && _ = False
True || _ = True
False || x = x
not :: Bool -> Bool
not True = False
not False = True
--------------------------------------------------------------------------
-- functions on Maybe
data Maybe a = Nothing | Just a
isJust :: Maybe a -> Bool
isJust (Just a) = True
isJust Nothing = False
isNothing :: Maybe a -> Bool
isNothing = not . isJust
fromJust :: Maybe a -> a
fromJust (Just a) = a
maybeToList :: Maybe a -> [a]
maybeToList Nothing = []
maybeToList (Just a) = [a]
listToMaybe :: [a] -> Maybe a
listToMaybe [] = Nothing
listToMaybe (a:_) = Just a
--------------------------------------------------------------------------
-- functions on pairs
fst :: (a,b) -> a
fst (x,y) = x
snd :: (a,b) -> b
snd (x,y) = y
curry :: ((a, b) -> c) -> a -> b -> c
curry f x y = f (x, y)
uncurry :: (a -> b -> c) -> ((a, b) -> c)
uncurry f p = f (fst p) (snd p)
--------------------------------------------------------------------------
-- functions on lists
map :: (a -> b) -> [a] -> [b]
map f xs = [ f x | x <- xs ]
(++) :: [a] -> [a] -> [a]
xs ++ ys = foldr (:) ys xs
filter :: (a -> Bool) -> [a] -> [a]
filter p xs = [ x | x <- xs, p x ]
concat :: [[a]] -> [a]
concat xss = foldr (++) [] xss
concatMap :: (a -> [b]) -> [a] -> [b]
concatMap f = concat . map f
head, last :: [a] -> a
head (x:_) = x
last [x] = x
last (_:xs) = last xs
tail, init :: [a] -> [a]
tail (_:xs) = xs
init [x] = []
init (x:xs) = x : init xs
null :: [a] -> Bool
null [] = True
null (_:_) = False
length :: [a] -> Int
length [] = 0
length (_:l) = 1 + length l
(!!) :: [a] -> Int -> a
(x:_) !! 0 = x
(_:xs) !! n = xs !! (n-1)
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs
iterate :: (a -> a) -> a -> [a]
iterate f x = x : iterate f (f x)
repeat :: a -> [a]
repeat x = xs where xs = x:xs
replicate :: Int -> a -> [a]
replicate n x = take n (repeat x)
cycle :: [a] -> [a]
cycle [] = error "Prelude.cycle: empty list"
cycle xs = xs' where xs' = xs ++ xs'
take, drop :: Int -> [a] -> [a]
take n _ | n <= 0 = []
take _ [] = []
take n (x:xs) = x : take (n-1) xs
drop n xs | n <= 0 = xs
drop _ [] = []
drop n (_:xs) = drop (n-1) xs
splitAt :: Int -> [a] -> ([a],[a])
splitAt n xs = (take n xs, drop n xs)
takeWhile, dropWhile :: (a -> Bool) -> [a] -> [a]
takeWhile p [] = []
takeWhile p (x:xs)
| p x = x : takeWhile p xs
| otherwise = []
dropWhile p [] = []
dropWhile p xs@(x:xs')
| p x = dropWhile p xs'
| otherwise = xs
lines, words :: String -> [String]
-- lines "apa\nbepa\ncepa\n" == ["apa","bepa","cepa"]
-- words "apa bepa\n cepa" == ["apa","bepa","cepa"]
unlines, unwords :: [String] -> String
-- unlines ["apa","bepa","cepa"] == "apa\nbepa\ncepa"
-- unwords ["apa","bepa","cepa"] == "apa bepa cepa"
reverse :: [a] -> [a]
reverse = foldl (flip (:)) []
and, or :: [Bool] -> Bool
and = foldr (&&) True
or = foldr (||) False
any, all :: (a -> Bool) -> [a] -> Bool
any p = or . map p
all p = and . map p
elem, notElem :: (Eq a) => a -> [a] -> Bool
elem x = any (== x)
notElem x = all (/= x)
lookup :: (Eq a) => a -> [(a,b)] -> Maybe b
lookup key [] = Nothing
lookup key ((x,y):xys)
| key == x = Just y
| otherwise = lookup key xys
sum, product :: (Num a) => [a] -> a
sum = foldl (+) 0
product = foldl (*) 1
maximum, minimum :: (Ord a) => [a] -> a
maximum [] = error "Prelude.maximum: empty list"
maximum xs = foldl1 max xs
minimum [] = error "Prelude.minimum: empty list"
minimum xs = foldl1 min xs
zip :: [a] -> [b] -> [(a,b)]
zip = zipWith (,)
zipWith :: (a->b->c) -> [a]->[b]->[c]
zipWith z (a:as) (b:bs)
= z a b : zipWith z as bs
zipWith _ _ _ = []
unzip :: [(a,b)] -> ([a],[b])
unzip = foldr (\(a,b) ~(as,bs) -> (a:as,b:bs)) ([],[])
nub :: Eq a => [a] -> [a]
nub [] = []
nub (x:xs) = x : nub [ y | y <- xs, x /= y ]
delete :: Eq a => a -> [a] -> [a]
delete y [] = []
delete y (x:xs) = if x == y then xs else x : delete y xs
(\\) :: Eq a => [a] -> [a] -> [a]
(\\) = foldl (flip delete)
union :: Eq a => [a] -> [a] -> [a]
union xs ys = xs ++ (ys \\ xs)
intersect :: Eq a => [a] -> [a] -> [a]
intersect xs ys = [ x | x <- xs, x `elem` ys ]
intersperse :: a -> [a] -> [a]
-- intersperse 0 [1,2,3,4] == [1,0,2,0,3,0,4]
transpose :: [[a]] -> [[a]]
-- transpose [[1,2,3],[4,5,6]] == [[1,4],[2,5],[3,6]]
partition :: (a -> Bool) -> [a] -> ([a],[a])
partition p xs = (filter p xs, filter (not . p) xs)
group :: Eq a => [a] -> [[a]]
-- group "aapaabbbeee" == ["aa","p","aa","bbb","eee"]
isPrefixOf, isSuffixOf :: Eq a => [a] -> [a] -> Bool
isPrefixOf [] _ = True
isPrefixOf _ [] = False
isPrefixOf (x:xs) (y:ys) = x == y && isPrefixOf xs ys
isSuffixOf x y = reverse x `isPrefixOf` reverse y
sort :: (Ord a) => [a] -> [a]
sort = foldr insert []
insert :: (Ord a) => a -> [a] -> [a]
insert x [] = [x]
insert x (y:xs) = if x <= y then x:y:xs else y:insert x xs
--------------------------------------------------------------------------
-- functions on Char
type String = [Char]
toUpper, toLower :: Char -> Char
-- toUpper 'a' == 'A'
-- toLower 'Z' == 'z'
digitToInt :: Char -> Int
-- digitToInt '8' == 8
intToDigit :: Int -> Char
-- intToDigit 3 == '3'
ord :: Char -> Int
chr :: Int -> Char
isDigit :: Char -> Bool
--------------------------------------------------------------------------
-- input/output
putStr :: String -> IO ()
getLine :: IO String
readFile :: FilePath -> IO String
writeFile :: FilePath -> String -> IO ()
--------------------------------------------------------------------------