Updates (2016): requirement to run and follow the advice from the

hlint

command for Part II.

In this Lab Assignment, you will design a Haskell program that will be able to solve Sudokus, a popular logical puzzle originating from Japan.

Assignments and Deadlines (2016)

There are 6 regular assignments as part of this Lab: A, B, C, D, E, and F. The lab consists (again) of two parts.

Assignments A, B, and C form Part I of the lab, and need to be submitted before Monday, September 26 at 12:00.

Assignments D, E and F form Part II of the Lab, and need to be submitted before Monday, October 3 at 12:00.

New (2016): For submitting Part 2 of the lab we expect you to run the

hlint

command on your program and followed the advice. If you do not understand the advice you should include the suggested code in comments in your submission.

There are also extra assignments X, Y, Z, P, and Q. You can choose freely whether to do one of these.

The final deadline for submitting this lab is Wednesday, October 12 at 23:59.

Hints

Some assignments have hints. Often, these involve particular standard Haskell functions that you could use. Some of these functions are defined in modules that you have to import yourself explicitly. You can use the following resources to find more information about those functions:

• Hoogle, the library function search engine

• Haskell Library Structure, all standard libraries, for you to browse

• A Tour of the Haskell Prelude shows all standard Haskell functions that you get without importing any module

We encourage you to actually go and find information about the functions that are mentioned in the hints!

Preparation

Before starting on this lab, make sure that you have understood the material from the lectures in week 1 to 4. It is not necessary to use higher-order functions to solve the lab, but there are some tasks in which certain higher-order functions may come in handy.

You should also be familiar with the Maybe type.

Some general hints:

• In order to “do something” with each row in a sudoku, use list comprehension:
  [... | r <- rows sud]

• To operate on the columns instead, use the function

  transpose :: [[a]] -> [[a]]  -- import Data.List

  to turn the list of rows into a list of columns.

• An alternative to list comprehension is to use the higher-order function

  map :: (a -> b) -> [a] -> [b]

• There are two ways to check that all elements in a sudoku satisfy some property:

  • Use list comprehension and one of the functions

    and :: [Bool] -> Bool  -- All elements are true?
    or  :: [Bool] -> Bool  -- Some element is true?

  • Use one of the higher-order functions

    all :: (a -> Bool) -> [a] -> Bool  -- All elements satisfy the property?
    any :: (a -> Bool) -> [a] -> Bool  -- Some element satisfies the property?

• Try to minimize the use of IO instructions and do as much work as possible using pure functions. For example, this program

  prog = putStr $ unlines ["line1", "line2"]

  is better than

  prog = do
      putStrLn "line1"
      putStrLn "line2"

Sudokus

Sudoku is a logic puzzle, originally coming from Japan. In the Western world, it has caught on in popularity enormously over the last couple of years. Most newspapers now publish a Sudoku puzzle for the readers to solve every day.

A Sudoku puzzle consists of a 9x9 grid. Some of the cells in the grid have digits (from 1 to 9), others are blank. The objective of the puzzle is to fill in the blank cells with digits from 1 to 9, in such a way that every row, every column and every 3x3 block has exactly one occurrence of each digit 1 to 9.

Here is an example of a Sudoku puzzle:

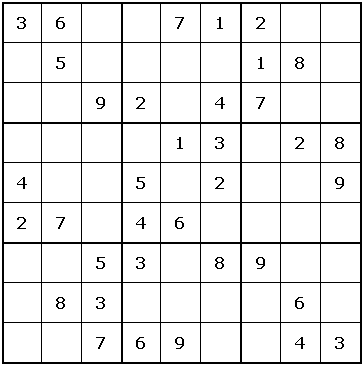
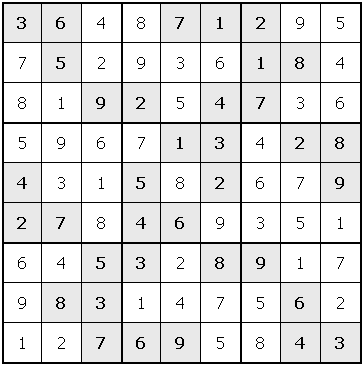
And here is the solution:

In this lab assignment, you will write a Haskell program that can read in a Sudoku puzzle and solve it.

More Information

If you want to read more about Sudokus, here are a few links:

Modelling Sudokus

To implement a Sudoku-solving program, we need to come up with a way of modelling Sudokus. A Sudoku is a matrix of digits or blanks. The natural way of modelling a matrix is as a list of lists. The outer list represents all the rows, and the elements of the list are the elements of each row. Digits or blanks can be represented by using the Haskell Maybe type. Digits are simply represented by Int.

Summing up, a natural way to represent Sudokus is using the following Haskell datatype:

data Sudoku = Sudoku [[Maybe Int]]

Since it is convenient to have a function that extracts the actual rows from the Sudoku, we say:

rows :: Sudoku -> [[Maybe Int]]
rows (Sudoku rs) = rs

For example, the above Sudoku puzzle has the following representation in Haskell:

example :: Sudoku
example =
  Sudoku
    [ [Just 3, Just 6, Nothing,Nothing,Just 7, Just 1, Just 2, Nothing,Nothing]
    , [Nothing,Just 5, Nothing,Nothing,Nothing,Nothing,Just 1, Just 8, Nothing]
    , [Nothing,Nothing,Just 9, Just 2, Nothing,Just 4, Just 7, Nothing,Nothing]
    , [Nothing,Nothing,Nothing,Nothing,Just 1, Just 3, Nothing,Just 2, Just 8]
    , [Just 4, Nothing,Nothing,Just 5, Nothing,Just 2, Nothing,Nothing,Just 9]
    , [Just 2, Just 7, Nothing,Just 4, Just 6, Nothing,Nothing,Nothing,Nothing]
    , [Nothing,Nothing,Just 5, Just 3, Nothing,Just 8, Just 9, Nothing,Nothing]
    , [Nothing,Just 8, Just 3, Nothing,Nothing,Nothing,Nothing,Just 6, Nothing]
    , [Nothing,Nothing,Just 7, Just 6, Just 9, Nothing,Nothing,Just 4, Just 3]
    ]

Now, a number of assignments follows, which will lead you step-by-step towards an implementation of a Sudoku-solver.

Some Basic Sudoku Functions

To warm up, we start with a number of basic functions on Sudukos.

Assignment A

A1. Implement a function allBlankSudoku :: Sudoku that represents a Sudoku that only contains blank cells (this means that no digits are present). Do not use copy-and-paste programming here! Your definition does not need to be longer than a few short lines.

A2. The Sudoku type we have defined allows for more things than Sudokus. For example, there is nothing in the type definition that says that a Sudoku has 9 rows and 9 columns, or that digits need to lie between 1 and 9. Implement a function isSudoku :: Sudoku -> Bool that checks if all such extra conditions are met by the given Sudoku. Examples: Sudoku> isSudoku (Sudoku []) False Sudoku> isSudoku allBlankSudoku True Sudoku> isSudoku example True Sudoku> isSudoku (Sudoku (tail (rows example))) False

A3. Our job is to solve Sudokus. So, it would be handy to know when a Sudoku is solved or not. We say that a Sudoku is solved if there are no blank cells left to be filled in anymore. Implement the following function: isSolved :: Sudoku -> Bool Note that we do not check here if the Sudoku is a valid solution; we will do this later. This means that any Sudoku without blanks (even Sudokus with the same digit appearing twice in a row) is considered solved by this function!

Hints

To implement the above, use list comprehensions! Also, the following standard Haskell functions might come in handy:

replicate :: Int -> a -> [a]
length    :: [a] -> Int
and       :: [Bool] -> Bool

See also the general hints above.

To help you get started, ahere is a file that you can use:

Reading and Printing Sudokus

Next, we need to have a way of representing Sudokus in a file. In that way, our program can read Sudokus from a file, and it is easy for us to create and store several Sudoku puzzles.

The following is an example text-representation that we will use in this assignment. It actually represents the example above.

36..712..
.5....18.
..92.47..
....13.28
4..5.2..9
27.46....
..53.89..
.83....6.
..769..43

There are 9 lines of text in this representation, each corresponding to a row. Each line contains 9 characters. A digit 1 – 9 represents a filled cell, and a period (.) represents a blank cell.

Assignment B

B1. Implement a function: printSudoku :: Sudoku -> IO () that, given a Sudoku, creates instructions to print the Sudoku on the screen, using the format shown above. Example: Sudoku> printSudoku allBlankSudoku ......... ......... ......... ......... ......... ......... ......... ......... ......... Sudoku> printSudoku example 36..712.. .5....18. ..92.47.. ....13.28 4..5.2..9 27.46.... ..53.89.. .83....6. ..769..43

B2. Implement a function: readSudoku :: FilePath -> IO Sudoku that, given a filename, creates instructions that read the Sudoku from the file, and deliver it as the result of the instructions. You may decide yourself what to do when the file does not contain a representation of a Sudoku. Recall from the IO lecture that FilePath is equivalent to String. Examples: Sudoku> sud <- readSudoku "example.sud" Sudoku> printSudoku sud 36..712.. .5....18. ..92.47.. ....13.28 4..5.2..9 27.46.... ..53.89.. .83....6. ..769..43 Sudoku> readSudoku "Sudoku.hs" Exception: Not a Sudoku! (Note: In the above example, we make use of the fact that commands in GHCi are part of an implicit do block. This allows us to bind results of IO instructions, just like in do notation: sud <- readSudoku …)

Hints

To implement the above, you will need to be able to convert between characters (type Char) and digits/integers (type Int). The standard functions intToDigit and digitToInt (import the module Data.Char) will come in handy here.

Here are some functions that might come in handy:

intToDigit :: Int -> Char
digitToInt :: Char -> Int
putStr     :: String -> IO ()
putStrLn   :: String -> IO ()
sequence_  :: [IO a] -> IO ()
readFile   :: FilePath -> IO String
lines      :: String -> [String]
unlines    :: [String] -> String

Here are some example Sudoku-files that you can download and use:

Generating Sudokus as Test Data

Finally, we need to be able to test properties about the functions related to our Sudokus. In order to do so, QuickCheck needs to be able to generate arbitrary Sudokus.

Let us split this problem into a number of smaller problems. First, we need to know how to generate arbitrary cell values (of type Maybe Int). Then, we need to know how to generate 81 such cells, and compose them all into a Sudoku.

Assignment C

cell :: Gen (Maybe Int)

Sudoku> sample cell
Just 3
Nothing
Nothing
Just 7
Nothing

C2. Make Sudokus an instance of the class Arbitrary. instance Arbitrary Sudoku where ... We have already done this for you in the file Sudoku.hs.

C3. Define a property prop_Sudoku :: Sudoku -> Bool that expresses that each generated Sudoku actually is a Sudoku according to Assignment A2. Also use QuickCheck to check that the property actually holds for all Sudokus that are generated.

Hints

Here are some functions that might come in handy:

sample    :: Gen a -> IO ()
choose    :: Random a => (a,a) -> Gen a
frequency :: [(Int,Gen a)] -> Gen a
sequence  :: [Gen a] -> Gen [a]

You might want to take a look at the lecture notes and example code on test data generation.

Rows, Columns, Blocks

Now, we are going to think about what actually constitutes a valid solution of a Sudoku. There are three constraints that a valid solution has to forfill:

type Block = [Maybe Int]

We are going to define a function that checks if a Sudoku is not violating any of the above constraints, by checking that none of the blocks violate those constraints.

Assignment D

isOkayBlock :: Block -> Bool

Sudoku> isOkayBlock [Just 1, Just 7, Nothing, Nothing, Just 3, Nothing, Nothing, Nothing, Just 2]
True
Sudoku> isOkayBlock [Just 1, Just 7, Nothing, Just 7, Just 3, Nothing, Nothing, Nothing, Just 2]
False

D2. Implement a function: blocks :: Sudoku -> [Block] that, given a Sudoku, creates a list of all blocks of that Sudoku. This means: 9 rows, 9 columns, 9 3x3 blocks. Also add a property that states that, for each Sudoku, there are 3*9 blocks, and each block has exactly 9 cells.

D3. Now, implement a function: isOkay :: Sudoku -> Bool that, given a Soduko, checks that all rows, colums and 3x3 blocks do not contain the same digit twice. Examples: Sudoku> isOkay allBlankSudoku True Sudoku> do sud <- readSudoku "example.sud"; print (isOkay sud) True

Hints

Here are some functions that might come in handy:

nub       :: Eq a => [a] -> [a]
transpose :: [[a]] -> [[a]]
take      :: Int -> [a] -> [a]
drop      :: Int -> [a] -> [a]

Note that some of the above functions only appear when you import Data.List.

See also the general hints above.

You might want to take a look at the exercises and answers on lists and list comprehensions.

Positions and Finding Blanks

We are getting closer to the final solving function. Let us start thinking about how such a function would work.

Given a Sudoku, if there are no blanks left in the Sudoku, we are done. Otherwise, there is at least one blank cell that needs to be filled in somehow. We are going to write functions to find and manipulate such a blank cell.

It is quite natural to start to talk about positions. A position is a coordinate that identifies a cell in the Sudoku. Here is a way of modelling coordinates:

type Pos = (Int,Int)

We use positions as indicating first the row and then the column. It is common in programming languages to start counting at 0! Therefore, the position that indicates the upper left corner is (0,0), and the position indicating the lower right corner is (8,8). And, for example, the position (3,5) denotes the 6th cell in the 4th row.

Assignment E

E1. Implement a function: blank :: Sudoku -> Pos that, given a Sudoku that has not yet been solved, returns a position in the Sudoku that is still blank. If there are more than one blank position, you may decide yourself which one to return. Examples: Sudoku> blank allBlankSudoku (0,0) Sudoku> blank example (0,2) Also write a property that states that the cell at the blank position is actually blank.

E2. Implement a function: (!!=) :: [a] -> (Int,a) -> [a] that, given a list, and a tuple containing an index in the list and a new value, updates the given list with the new value at the given index. Examples: Sudoku> ["a","b","c","d"] !!= (1,"apa") ["a","apa","c","d"] Sudoku> ["p","qq","rrr"] !!= (0,"bepa") ["bepa","qq","rrr"] Also write (a) propert(y/ies) that state(s) the expected properties of this function. Think about what can go wrong!

E3. Implement a function: update :: Sudoku -> Pos -> Maybe Int -> Sudoku that, given a Sudoku, a position, and a new cell value, updates the given Sudoku at the given position with the new value. Example: Sudoku> printSudoku (update allBlankSudoku (1,3) (Just 5)) ......... ...5..... ......... ......... ......... ......... ......... ......... ......... Also write a property that checks that the updated position really has gotten the new value.

Hints

There is a standard function (!!) in Haskell for getting a specific element from a list. It starts indexing at 0, so for example to get the first element from a list xs, you can use xs !! 0.

We usually use the standard function zip to pair up elements in a list with their corresponding index. Example:

*Main> ["apa","bepa","cepa"] `zip` [1..3]
[("apa",1),("bepa",2),("cepa",3)]

This, in combination with list comprehensions, should be very useful for this assignment!

When testing a property that is polymorphic (meaning that it has type variables in its type), you need to add a type signature that picks an arbitrary type. For example, when testing properties for the function (!!=), which works for lists of any type, you have to fix the type when testing, for example lists of Integers. Do this by adding a type signature to your properties.

Here are some more useful functions:

head :: [a] -> a
(!!) :: [a] -> Int -> a
zip  :: [a] -> [b] -> [(a,b)]

You might want to take a look at the exercises and answers on lists and list comprehensions.

Solving Sudokus

Finally, we have all the bits in place to attack our main problem: Solving a given Sudoku.

Our objective is to define a Haskell function

solve :: Sudoku -> Maybe Sudoku

1. sud violates some of the constraints (in other words: some of its blocks contain the same digit twice). In this case, the answer of solve must be Nothing.

2. sud does not contain any blanks (in other words: sud is a solution!). In this case, the answer of solve must be Just sud.

3. Otherwise, sud must contain at least one blank cell. In this case, we try to recursively solve sud 9 times; each time we update the blank cell with a concrete digit from 1 to 9. The first recursive attempt that succeeds is our answer. If none of the recursive attempts succeed, we return Nothing.

This method of problem solving is called backtracking.

Since backtracking is not covered in the course, we provide you with a skeleton implementation of the solver. If you want more challenge, don’t look at the code provided here!

The solver is a function

solve :: Sudoku -> Maybe Sudoku

which receives a sudoku that may not be solved and, if possible, returns a solved sudoku. The idea is that solve will either return immediately – if there’s a violation or if the sudoku is already solved – or it will call itself recursively according to the method above:

solve :: Sudoku -> Maybe Sudoku
solve s | ...       = Nothing  -- There's a violation in s
        | ...       = Just s   -- s is already solved
        | otherwise = pickASolution possibleSolutions
  where
    nineUpdatedSuds   = ... :: [Sudoku]
    possibleSolutions = [solve s' | s' <- nineUpdatedSuds]

The final case is the tricky one. First, we have the local definition nineUpdatedSuds, which is a list of nine sudokus. They should all be the same as the sudoku s, except that the first blank cell should be updated from Nothing to a numeric value. Since the cell can be updated in nine different ways, we get a list of nine new sudokus.

By recursively solving these nine sudokus, we get a list of nine possible solutions (possibleSolutions). Now it’s just the task of the helper function pickASolution to pick one of them (if there is one):

pickASolution :: [Maybe Sudoku] -> Maybe Sudoku
pickASolution suds = ...

A key to understanding this definition of solve is to realize that solve can only return Nothing or a completely solved sudoku, as seen in the two base cases. This means that any Just value in possibleSolutions has to be a complete solution.

Another key is to see that each call to solve must reach one of the base cases sooner or later, because in every recursive call we take away one blank cell. Taking away a blank cell means making progress towards a solution or a conflict.

Assignment F

F1. Implement a function: solve :: Sudoku -> Maybe Sudoku using the above idea. Unless you’re up for a challenge you are recommended to use the skeleton code from above and just fill in the ... parts. Examples: Sudoku> printSudoku (fromJust (solve allBlankSudoku)) 123456789 456789123 789123456 214365897 365897214 897214365 531642978 642978531 978531642 Sudoku> do sud <- readSudoku "example.sud"; printSudoku (fromJust (solve sud)) 364871295 752936184 819254736 596713428 431582679 278469351 645328917 983147562 127695843 Sudoku> do sud <- readSudoku "impossible.sud"; print (solve sud) Nothing (In the above examples, we use the standard function fromJust from the library Data.Maybe.)

F2. For your own convenience, define a function: readAndSolve :: FilePath -> IO () that produces instructions for reading the Sudoku from the given file, solving it, and printing the answer. Examples: Sudoku> readAndSolve "example.sud" 364871295 752936184 819254736 596713428 431582679 278469351 645328917 983147562 127695843 Sudoku> readAndSolve "impossible.sud" (no solution)

F3. Implement a function: isSolutionOf :: Sudoku -> Sudoku -> Bool that checks, given two Sudokus, whether the first one is a solution (i.e. all blocks are okay, there are no blanks), and also whether the first one is a solution of the second one (i.e. all digits in the second sudoku are maintained in the first one). Examples: Sudoku> fromJust (solve allBlankSudoku) `isSolutionOf` allBlankSudoku True Sudoku> allBlankSudoku `isSolutionOf` allBlankSudoku False Sudoku> fromJust (solve allBlankSudoku) `isSolutionOf` example False

F4. Define a property: prop_SolveSound :: Sudoku -> Property that says that the function solve is sound. Soundness means that every supposed solution produced by solve actually is a valid solution of the original problem.

Hints

All the work we did in the assignments A – E should be used in order to implement the function solve.

To implement the third, recursive, case of solve, you can use a list comprehension that enumerates all possible values for the blank cell. You can then use the standard function listToMaybe to turn the result into something of type Maybe.

QuickChecking the property prop_SolveSound will probably take a long time. Be patient! Alternatively, there are a number of things you can do about this.

fewerCheck prop = quickCheckWith stdArgs{ maxSuccess = 30 } prop

It is okay if you do not find a completely satisfactory solution to this.

Here are some useful functions:

fromJust    :: Maybe a -> a
listToMaybe :: [a] -> Maybe a

Here is an example of an impossible Sudoku:

Extra Assignments

You can choose freely whether to do 0, 1 or more of these.

There are no perfect, pre-defined answers here, but try to show your thoughts and understanding in your answers.

Extra Assignments

These are not obligatory, but you will learn more if you do them!

X. The solving method we have used in this lab assignment is very basic, and in some sense naive. One way to boost performance is to look closer at the function blank. Perhaps if we picked the blank in a smarter way, the solve function would go faster? One idea is to always pick the blank spot where there are as few possibilities left. For example, if we have a row with one or two blank spots, it is probably a good idea to pick one of those blank spots, since it will limit the consecutive search most, and it will lead to search to a state with more digits filled in. (Such a way of changing a solving method is called a heuristic – there is no absoluate guarantee that the search will go faster, but often it actually will.) Change the implementation of the blank function, so that it always picks the blank spot that is in a row, column, or 3x3 block where there are as few blank spots left. For example, in the Sudoku below: 36..712.. .5....18. ..92.47.. ...x13.28 4..5.2..9 27.46.... ..53.89.. .83....6. ..769..43 we have marked one blank spot with an x. The row in which this x is has 5 blank spots (including the x itself); the column in which this x is has 4 blank spots, and the 3x3 block in which this x is has 3 blank spots. It turns out that this is the best we can do; it is good to pick x as the next blank spot, since there will only be 2 blank spots left in the middle 3x3 block. Does your solve function work faster now? Experiment with different heuristics (for example: only look at rows and columns, and not at 3x3 blocks), and see which one performs best. Can you solve some of the hard Sudokus now? Do not forget to add appropriate properties that test your functions.

Y. The solving method we have used in this lab assignment is very basic, and in some sense naive. The best known methods to solve problems like Sudoku is to also include the notion of propagation. This is the way most humans actually solve a Sudoku. A simple variant of propagation is the following. Suppose we have Sudoku with a row with precisely one blank, such as the 3rd row in the example below: 36..712.. .5....18. ..92.47.. 596.13428 4..5.2..9 27.46.... ..53.89.. .83....6. ..769..43 Our current solution would go and pick blanks, and start searching recursively, without making use of the fact that we already know the value of that blank (namely 7 in this case); all the other values have been used by the other cells in the row. Implement a function propagate :: Sudoku -> Sudoku that, given a Sudoku, finds out which rows, columns, and 3x3 blocks only have one blank in them, and then fills those blanks with the only possibly remaining value. It repeats doing this until all rows, columns and 3x3 blocks are either completely filled up, or contain two holes or more. Now, add this function at the appropriate place in your solve function. Does it work faster now? For other, more powerful propagation, you can for example read the following webpage: sudoku.com, and click on “how to solve”. Or come up with your own propagation rules! Do not forget to add appropriate properties that test your functions.

Z. Write a function that produces interesting Sudoku puzzles. For example, one could have a function createSudoku :: IO () that every time we run it, would print a new, interesting Sudoku puzzle on the screen. One can discuss what an interesting Sudoku puzzle is. Here are three properties that an interesting Sudoku puzzle must have: There must be a solution There must not be two different solutions There must not be too many digits already visible Can you think of a way to define a function for generating an infinite supply of new Sudokus satisfying the above two properties? You should of course make use of the functions you already have. Do not forget to add appropriate properties that test your functions.

P. Generalize the Sudokus that are dealt with in this assignment to other dimensions, for example 4x4 Sudokus, or 4x3 Sudokus. Do all dimensions make sense? Make sure your solution works in general, for all possible dimensions that make sense. For inspiration, look here: Monster Sudokus. Or here: xkcd comics :-) Do not forget to add appropriate properties that test your functions.

Q. We have stated the soundness of the solve function as a property; every produced solution should be a real solution. The dual of soundness is completeness. Completeness says that whenever there is a solution, the solve function should also produce a solution. (Equivalently, if the solve function says that there is no solution, then there really is no solution.) If we define the following helper datatype: data SolvableSudoku = Solvable Sudoku Then, implement a property prop_SolveComplete :: SolvableSudoku -> Bool prop_SolveComplete (Solvable sud) = ... that states that, for any solvale Sudoku, solve produces an answer. Now, make the type SolvableSudoku an instance of Arbitrary: instance Arbitrary SolvableSudoku where arbitrary = ... Here, you need to think about how to generate arbitrary Sudokus that are guaranteed to be solvable! One idea is to start with an arbitrary solved Sudoku, and randomly blank out some of the digits. Implement this!

Submission

Submit your solutions using the Fire system.

Your submission should consist of the following files:

Before you submit your code, Clean It Up! Remember, submitting clean code is Really Important, and simply the polite thing to do. After you feel you are done, spend some time on cleaning your code; make it simpler, remove unneccessary things, etc. We will reject your solution if it is not clean. Clean code:

New (2016): For submitting Part II of the lab we expect you to run the

hlint

command on your program and follow the advice. If you are not able to understand the advice you should at least include the code suggested by hlint in comments in your submission.

To the Fire System

Once you have submitted, please arrange to present your solution to one of the course assistants according to the instructions on the lab overview page.

Good Luck!