| Functional Programming -- 2009 Lab Assignment 4 | TDA452 & DIT142 | LP2 | HT2011 | [Home] |
In this Lab Assignment, you will design and implement a very simple graphical calculator.
The idea is to use the standard library Gtk2Hs for the graphical part.
Assignments and Deadlines
In this lab, you have a little bit more freedom than in the previous labs; we will not guide you towards a solution as much as in the previous lab assignments. The lab consists (again) of two parts.
Hints
Some assignments have hints. Often, these involve particular standard Haskell functions that you could use. Some of these functions are defined in modules that you have to import yourself explicitly. You can use the following resources to find more information about those functions:
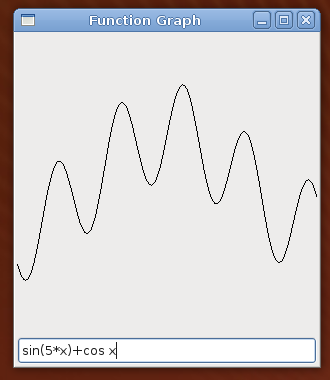
We encourage you to actually go and find information about the functions that are mentioned in the hints!The graphical calculator you are going to implement is a program that produces a window that might look like this:

The window consists of a drawing area, and a text entry field below it. The user can type mathematical expressions in the text entry, which, after pressing return, will be graphically shown on the drawing area.
The lab assignment consists of two parts. In Part A, you will implement the parts of your program that have to do with expressions. In part B, you will implement the graphical part of your program.
In this part, you are going to design a datatype for modelling mathematical expressions containing a variable x. For example:
In other words, an expression consists of: You will also implement a number of useful functions over this datatype.Put your answers to part A in a module called Expr.hs and submit in the usual way.
Part A: Assignments A-E
| A. Design a (recursive) datatype Expr that represents expressions of the above kind. Design your datatype (and program) so that it would be easy to extend the language with more functions that just sin and cos. |
B. Implement a function
showExpr :: Expr -> Stringthat converts any expression to a string. You should use as few parentheses as possible (see the comments below). The strings that are produced should look something like the example expressions shown earlier. If you want to, you can from now on use this function as the default show function by making Expr an instance of the class Show:
instance Show Expr where
show = showExpr
But you do not have to do this.
|
C. Implement a function
eval :: Expr -> Double -> Doublethat, given an expression, and the value for the variable x, calculates the value of the expression. |
D. Implement a function
readExpr :: String -> Maybe Exprthat, given a string, tries to interpret the string as an expression, and returns Just of that expression if it succeeds. Otherwise, Nothing will be returned. You are required to use the module Parsing.hs to construct this function. |
The last assignment is about checking that your definition of readExpr matches up with your definition of showExpr. One could define a property that simply checks that, for any expression e1, if you show it, and then read it back in again as an expression e2, then e1 and e2 should be the same.
However, this is too strict; there is certain information loss in showing an expression. For example, the expressions "(1+2)+3" and "1+(2+3)" have different representations in your datatype (and are not equal), but showing them yields "1+2+3" for both.
E. Write a property
prop_showReadExpr :: Expr -> Boolthat says that first showing, then reading, and then showing an expression (using your functions showExpr and readExpr) should produce the same result as simply showing the expression (again using your function showExpr). Also define a generator for expressions: arbExpr :: Int -> Gen ExprDo not forget to take care of the size argument in the generator. Make Expr an instance of the class Arbitrary and QuickCheck the result!
instance Arbitrary Expr where
arbitrary = sized arbExpr
|
Hints
* To design the datatype, you might be inspired by the Expr datatype discussed in the lectures in the lectures of Week 4. Read the slides and look at the example code! You should try not to add more constructors to your datatype than you really need.
* When showing expressions you are required to only add brackets:
In all other cases, you do not have to require parentheses. For example:For the functions eval, showExpr, readExpr and arbExpr, also read the slides for that week, and look at the example code that is provided.
For the function readExpr, to be able to parse floating point numbers (Doubles) and sin and cos, you only have to change the parser for factors.
For the function readExpr, to allow spaces in the expression, simply filter out all spaces from the string before you use the parser. In this way, spaces will not mess up your parser and keep it nice and clean.
When writing the property prop_showReadExpr, make sure that the property you define will not crash, even if there is something wrong with your functions! A common way for the property to crash is when the readExpr function (unexpectedly) delivers Nothing. Instead of crashing, your property should return False in that case. You can do this by doing a case expression on the result of readExpr, or by adding that the result of readExpr should not be equal to Nothing before you check that the result is of the shape Just e. Another thing to watch out for is rounding errors. Depending on how you implement prop_showReadExpr you may need to defined an approximate equality operator.
If you have a hard time understanding the generated counter examples for your property, it is probably a good idea to let Haskell derive the show function for your Expr datatype, instead of making your own instance of Show.
If your QuickCheck property crashes without you understanding why, you can use the function verboseCheck instead of the function quickCheck (type for example verboseCheck prop_Apa). In this way, all test data is shown before the test is being run. verboseCheck can be imported from this module.
In this part, you are going to implement the graphical part of the calculator. The graphical interface consists of two parts: (1) the drawing area, where the function is going to be drawn, and (2) the text entry field.
The drawing area is a panel widget of a certain size (you decide yourself, but let us suppose it has width and height of 300). A panel has a coordinate system that works in pixels. Here is how it works:
| (0,0) | (300,0) |
| (0,300) | (300,300) |
Perhaps surprising is that y-coordinates are upside down; they are 0 at the top, and 300 at the bottom.
The tricky thing using this panel to draw our functions is the following:
For example, the coordinate system for our functions might work like this:
| (-6.0,6.0) | (6.0,6.0) | |
| (0,0) | ||
| (-6.0,-6.0) | (6.0,-6.0) |
So, some conversion is needed between pixels (represented using Int) and floating point numbers (represented using Double).
The deadline for Part B is given on the home page. Put your answers for part B in a module called Calculator.hs. The module Calculator can of course import the module Expr.
In this part of the assignment, you will have to use Gtk2Hs. Make sure you write
import Graphics.UI.Gtk import Graphics.UI.Gtk.Gdk.GC import Exprat the top of your file Calculator.hs.
Part B: Assignments F-I
F. Implement a function with the following type.
points :: Expr -> Double -> (Int,Int) -> [Point]The function gets three arguments; points exp scale (width,height): The type Point is already defined, and is just a pair of integers: type Point = (Int,Int) The idea is that points will calculate all the points of the graph in terms of pixels. The scaling value tells you the ratio between pixels and floating point numbers. The arguments width and height tell you how big the drawing area is. We assume that the origin (0,0) point is in the middle of our drawing area. For the panel and function coordinate systems above, we would use 0.04 for the scale (since 1 pixel corresponds to 0.04 in the floating point world, this is (6.0 + 6.0) / 300), and (300,300) for the width and height. |
|
G. Implement the graphical user interface that connects assigments A-F
into a simple graphical calculator.
When the user types in something that is not an expression, you may decide yourself what to do. The easiest thing is to draw nothing. In addition, add a button which generates and displays a random expression. |
|
H.
Finally, you must chose and implement one [H(i) - H(iii)]
of the following extensions to the previous assignments.
|
Hints
To convert back and forth between Ints and Doubles, the following functions might come in handy:
round :: Double -> Int fromIntegral :: Int -> DoubleThese functions have more general types than the ones given above. For other conversion functions, use Hoogle!
To implement the function points, it is probably a good idea to define the following two local helper functions:
pixToReal :: Int -> Double -- converts a pixel x-coordinate to a real x-coordinate realToPix :: Double -> Int -- converts a real y-coordinate to a pixel y-coordinate
For an example use of the panels, and an example of how to build a graphical user interface, look at the examples provided in the lecture on Gtk2Hs. In particular:
In addition, Gtk2hs has predefined function:drawLines :: DrawableClass d => d -> GC -> [Point] -> IO ()(You might be interested in comparing the visual effect of this implementation with repeated application of the basic drawLine function.)
Note: for this lab you do not need to use any state variables to keep track of the state!
Submit your solutions using the Fire system.
Your submission should consist of the following files:
Before you submit your code, Clean It Up! Remember, submitting clean code is Really Important, and simply the polite thing to do. After you feel you are done, spend some time on cleaning your code; make it simpler, remove unneccessary things, etc. We will reject your solution if it is not clean. Clean code:
To the Fire System Good Luck!
| Original lab written and developed by Koen Lindström Claessen |